컴퓨터 그래픽스에서 좌표계 이해하기 (2024.01.22)
1. 개요
보통 우리는 컴퓨터 그래픽스라는 것을 생각할 땐 너무 복잡하게 생각하려는 경향이 있다. 개인적으로 필자는 그래픽스를 공부를 항상 실제 현실과 비유를 해서 했는데, 그게 좀 더 이해가 쉽고 편하기도 하고, 직관적이기도 하다. 대표적으로 컴퓨터 그래픽스에서 좌표계라는 개념의 경우 실제 카메라를 들고 세상을 촬영하는 사람을 생각하면 그 수많은 용어와 과정이 자연스레 이해가 될 것이다. 현실의 어떤 한 장면을 사진을 찍는다고 해보자. 어차피 동영상은 사진을 빠른 시간에 찍는 행위이므로 결국 사진 찍기에 포함되기에 사진으로만 대화를 국한시킬 것이다. 우리가 사진을 찍으려면 우선 찍으려는 피사체가 존재할 것이다. 예를 들어 여러분이 지금 스위스에 놀러가 알프스를 배경으로 사진을 찍으려고 한다고 하자. 거리를 좀 걷다보니 뒷 풍경이 아름다운 카페를 발견했다. 그곳에서 당신은 커피를 시키고 쉬고 있다. 순간 그 순간을 사진으로 남기고 싶어 진다. 카메라를 꺼내고 커피가 올려진 책상과 그 뒤로 펼쳐지는 푸르른 에메랄드 빛 호수와 눈으로 뒤덮힌 머리를 드러낸 알프스를 찍는다. 셔터를 누르는 순간 조리개 안으로 빛이 들어 오고, 카메라의 센서는 이 빛을 감지하여 디지털 필름에 기록하게 된다. 그 광활한 대지를 차지한 알프스의 풍경과 커피잔은 사진이라는 조그마한 데이터 쪼가리에 기록되는 것이다. 아무리 사진의 화질이 좋다고 하더라도 현실의 화질을 이길 수는 없을 것이다. 알프스의 한 나무 위에 있는 귀여운 새 한 마리는 당신의 사진의 한 픽셀도 차지하지 못 해서 사진에 찍히지 않게 될 수도 있다.
Woah, On a cruise ship
다시 정리해보자. 사진을 찍기 위해서는 우선 우리는 풍경이라는 피사체가 필요했고, 이를 찍기 위한 카메라가 필요했다. 우리는 원하는 사진을 찍기 위해 피사체의 위치와 카메라의 광각과 같은 설정과 위치를 결정해주었다. 그렇게 셔터를 누르면 우리가 원하는 사진이 나오게 된다. 이제 수학적인 얘기를 해보자. 어떤 피사체가 사진에 담겼다는 것은, 블랙 박스 f에 풍경의 한 점 x를 주었을 때 사진 위의 한 점 y으로 사상 되었다는 것이다. y라는 좌표는 사진이라는 점들의 집합에 포함된다. 만약 사진의 화질이 wpic × hpic이라고 치면 y = (xy, yy) ∈ { xy, yy | xy ∈ [0, wpic), yy ∈ [0, hpic) }가 된다. 이 점들의 집합, 즉 공간을 우리는 화면 공간screen space이라 부른다. 반대로 풍경은 이 세상의 어떤 공간에 존재하므로, 이 공간을 세상 공간world space라 부른다. 어떤 한 공간을 다른 공간으로 바꾸는 일련의 과정을 우리는 공간 변환space transformation이라 부른다.
2. 좌표계
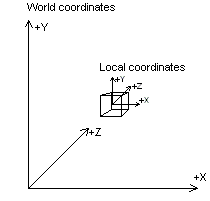
만약 기하와 벡터를 공부한 일반인이라면 z 축이 위아래, y 축이 앞뒤, x 축이 좌우를 의미하는 것이 자연스러울 것이다. 하지만 컴퓨터 그래픽스에서는 좀 다르다. 컴퓨터 그래픽스에서는 z와 y가 바뀐다. y가 위아래를, z가 앞뒤를 의미하게 된다. 그 이유를 이해하면 사실 자연스러운데, 컴퓨터 화면이라는 2차원 공간에서는 좌우가 x 축, 위아래가 y 축이 되는 건 자연스러울 것이다. 슈퍼 마리오와 같은 2D 게임을 할 땐 마리오가 좌우 x 축으로 움직이고, 위아래 y 축으로 점프를 할 것이다. 여기에 우리가 축 하나를 추가해서 3D 게임을 한다고 해보자. 이 경우에는 이미 우리가 y 축을 잘 위아래로 쓰고 있던 걸 굳이 z 축으로 대체하는 것보다는 일종의 깊이감을 주는 앞뒤 축을 z 축으로 사용하는 것이 자연스러울 것이다. 여기서 통상적으로 앞이라는 건 화면을 기준으로 플레이어를 바라보는 방향을 앞이라고 하고, 플레이어가 바라보는 방향이 뒤가 된다.
근데 여기서 x축이 좌우, z축이 앞뒤, y축이 위아래라고 표현을 했지, x의 양이 좌인지 우인지, y의 양이 위인지 아래인지, z의 양이 앞인지 뒤인지는 언급하지 않았다. 보통 컴퓨터 그래픽스에서는 이를 두고 크게 두 가지를 구분하는데, 우선 x축과 y축은 고정한 상태로 z축의 방향으로 구분한다. 즉, y의 양의 방향은 위, 음의 방향이 아래가 되고, x축의 양의 방향은 오른쪽, 음의 방향은 왼쪽이 된다. 이후 z의 양이 뒤냐, 앞이냐에 따라 좌수 좌표계left handed coordinate system와 우수 좌표계right handed coordinate system으로 나뉜다.

By Primalshell - Own work, CC BY-SA 3.0, Link
참고로 사용하는 Graphics API마다 handedness가 달라질 때가 있다. Direct3D의 경우 좌수 좌표계를 사용하고[1], OpenGL과 Vulkan은 우수 좌표계를 사용한다[2], [3].
3. 공간
3.1. 객체/모델 공간 Object/Model Space
우리 입장에서 보면 커피잔은 단순히 카페숍의 테이블 위에 올려져 있는 존재이지만, 커피잔 입장에서 보면 모든 세상은 커피잔을 중심으로 방위가 정해진다. 더 이상 커피잔은 “우리 앞”에 있는 존재가 아니고, 커피잔 입장에서 우리가 “커피잔 앞”에 있는 것이다. 이렇듯 모든 객체object 혹은 모델model은 자기만의 공간, 좌표계를 갖는다.
3.2. 세상 공간 World Space
하지만 객체 공간은 결국 자기 시점에서의 좌표계일 뿐이고, 세상을 하나로 봤을 때의 통일된 좌표계가 또 존재할 것이다. 지구의 경우에는 위도와 경도라는 이름으로 일종의 구면 좌표계를 사용하고 있다. 풍경에는 커피잔만 있는 것이 아니라 알프스도 있어야 하고, 호수도 있어야 하고 기타 등등 여러 객체/모델들이 서로 통일된 한 공간에 존재해야 한다. 이것이 바로 세상 공간이다.
3.3. 카메라/시점 공간 Camera/View Space
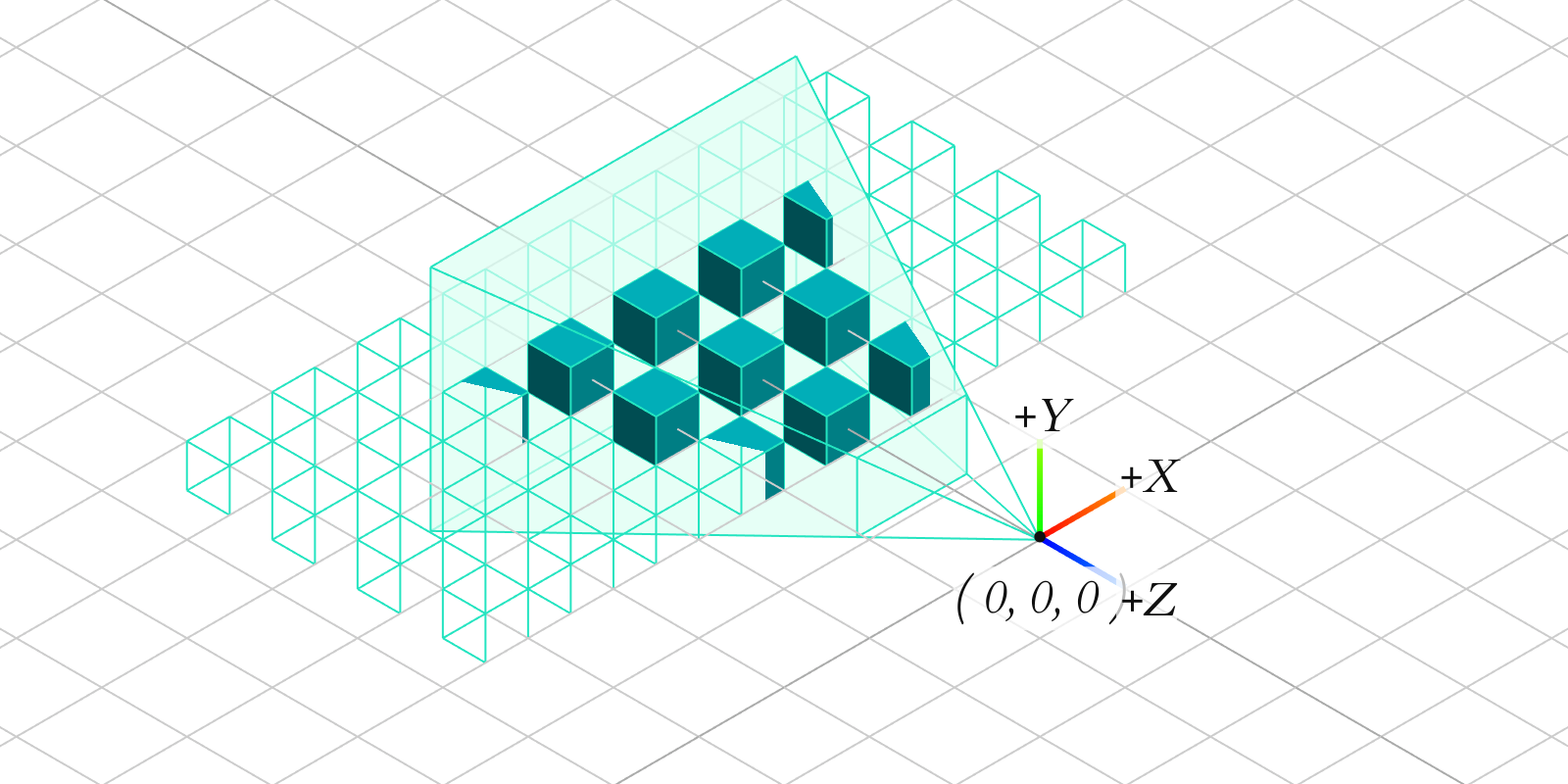
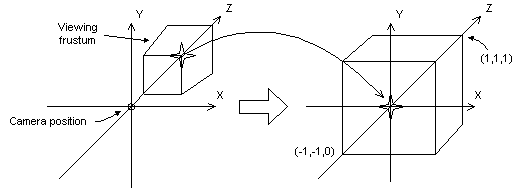
카메라 입장에서는 세상 공간을 전부 알 필요가 없다. 그저 카메라를 기준으로 카메라 프레임 안에 담길 수 있는 부분만이 필요할 뿐이고, 이를 기준으로하는 새로운 좌표계가 설정된다. 카메라를 기준으로 카메라보다 뒤에 있으며, 카메라의 센서와 렌즈 간의 거리, 렌즈의 크기와 센서의 비율 등에 따라 카메라에 담길 풍경을 결정한다. 이렇게 결정된 꼭대기가 잘린 형태의 피라미드를 각뿔대라 부르며, 시점에 의해 결정되었다고 해서 시점 각뿔대view frustum이라 부른다.
현실에서는 카메라가 찍을 수 있는 거리는 무한하지만, 컴퓨터 그래픽스에서는 그럴 수 없기 때문에 무한히 뒤로 연장되는 형태의 피라미드가 아닌 끝부분이 짤린 형태의 피라미드가 된다. 마찬가지로 센서라는 어떤 공간으로 빛을 받아야 하기 때문에 피라미드의 꼭지점보다 앞을 짤라 최종적으로 각뿔대가 생기는 것이다. 이때 카메라 가까이서 자른 단면을 근면near plane이라 부르고 끝부분을 자른 단면을 원면far plane이라 부른다.
3.4. 클립 공간/정규 시점 육면체/정규 장치 좌표 Clip Space/Canonical View Volume/Normalized Device Coordinates
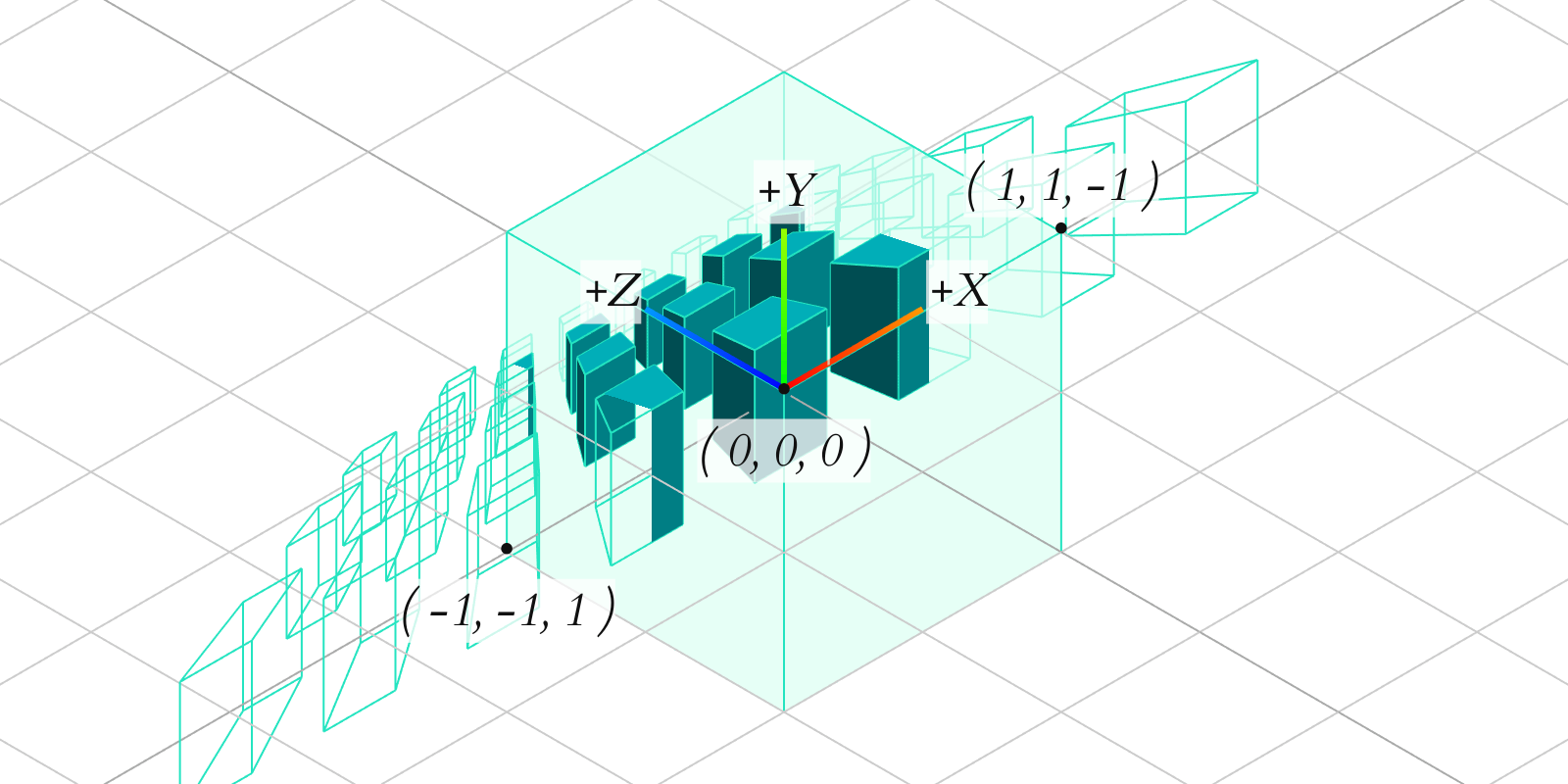
시점 각뿔대를 얻었다고 끝인게 아니다. 결국에는 이 정보가 사진이라는 2차원 정보로 압축이 되어야 한다. 이를 위해서는 근면과 원면을 정규화된 좌표로 변환을 시켜주어야 한다. 이때 최종적으로는 정(직)육면체 형태의 공간을 얻게 된다. 이때 이 공간은 x축과 y축으로 [-1, 1]의 범위로 정규화가 되지만, z축은 사용하는 Graphics API에 따라 [-1, 1]로 정규화를 하거나 [0, 1]의 범위로 정규화가 된다. Direct3D와 Vulkan은 후자로, OpenGL은 전자로 정규화를 한다.
당연히 근면보다 원면이 클테니, 이 둘의 크기를 정규화하면 위의 그림처럼 근면과 가까울 수록 크고, 원면과 가까울 수록 작은 형태의 결과를 얻게 된다. 이는 곧 원근감을 의미한다.
3.5. 화면 공간 Screen Space
최종적으로 얻은 육면체를 원면에서 근면 쪽으로 마치 유압 프레스를 하듯이 투영해주어 얻는 결과가 바로 화면 공간이다.
4. 변환
4.1. 모델 변환 Model Transformation
모델 변환은 단순히 한 모델을 자신만의 공간에서 게임 공간으로의 변환이므로, 필요한 translation, rotation, scaling 등을 수행해주면 된다. 예를 들어 마인크래프트와 같은 간단한 게임을 예시로 들면 필요한 건 translation만 있으면 된다. 고정된 크기의 정육면체 블록이 있다고 해보자. 그러면 각 블록이 게임 공간에서 어느 3차원 그리드에 속하는가에 따라 translation만 해주면 끝이다.
4.2. 카메라 변환 Camera Transformation
카메라를 원점으로 3D 축을 구축하면 된다. 우리에게 주어지는 정보는 1. 카메라의 위치, 2. 카메라가 바라보는 방향, 3. 카메라를 좌우로 나누는 임의의 평면 위의 한 벡터이다. 보통 1번을 eye 벡터, 2번을 at 벡터, 3번을 up 벡터라 부른다. 3번이 좀 어려울 수도 있는데, 의미적으로 보면 카메라가 위를 바라보는 방향이면 되지만, 생각보다 그러한 벡터를 구하기가 어려울 수도 있고, 수학적으로 반드시 그 방향에 해당하는 벡터가 필요한 것은 아니다. 축을 구하기 위해서는 단순히 카메라가 바라보는 방향 벡터와 카메라와 수직인, 위를 바라보는 방향 벡터 둘이 이루는 평면 위의 크기가 0이 아닌 임의의 벡터이기만 하면 된다(당연히 방향 벡터와는 달라야 한다).
이제 직접 좌표계를 구해보도록 하자. 사실 구하기 가장 쉬운 축은 바로 z 축이다. z 축이 무엇인가? 바로 앞 뒤를 의미하는 것이다. 그렇다면 카메라를 기준으로 z+ 축은 어디를 바라보는 걸까? 좌수 좌표계라면 카메라가 바라보는 방향이 될 것이고, 우수 좌표계라면 카메라가 바라보는 방향의 반대 방향이다. 그런데 카메라가 바라보는 방향? 이거 어디서 많이 들어보지 않았는가? 그렇다. 바로 at 벡터이다. 좌수 좌표계라면 at 벡터의 방향이 곧 z+ 축이 되는 것이고, 우수 좌표계에서는 z- 축이 된다. 물론 좌표계를 구한다는 것은 단위 기저가 필요하므로 정확한 수식은 좌수 좌표계에선:
\[\mathbf{view}_{z} = \frac{\mathbf{at}}{\left \| \mathbf{at} \right \|}\]이고 우수 좌표계에선:
\[\mathbf{view}_{z} = -\frac{\mathbf{at}}{\left \| \mathbf{at} \right \|}\]이다.
다음으로는 실제로 카메라의 위를 바라보는, 카메라와 수직인 y+ 축을 구해보자. 사실 이건 생각보다 수학적으로 간단하다. 방금 구한 z 축과 수직인 평면을 구하고, 해당 평면에 up 벡터를 투영하면 되기 때문이다!!
이 식을 구하기 위해서는 벡터의 중요한 한 가지 법칙을 기억하고 있으면 된다. 바로 벡터의 덧셈이다.
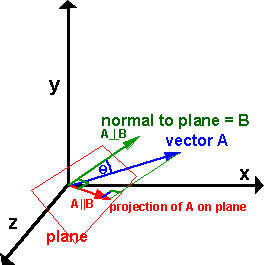
위의 그림에서 A와 B는 둘 다 원점 O를 지나고, B는 평면의 법선 벡터이고, A ∥ B는 A를 평면에 투영한 벡터이고, A ⊥ B는 A를 평면의 법선 벡터에 투영한 벡터이라고 하자. 이렇게 되면 $\mathbf{A} = \mathbf{A} \parallel \mathbf{B} + \mathbf{A} \perp \mathbf{B}$가 된다. 이때 A ⊥ B는 A 벡터를 B 벡터에 투영한 벡터이기 때문에 금방 구할 수 있다:
\[\mathbf{A} \perp \mathbf{B} = \frac{\mathbf{A} \cdot \mathbf{B}}{\left \| \mathbf{B} \right \|^{2}}\mathbf{B}\]우리가 궁극적으로 구하려는 값은 A ∥ B이므로,
\(\mathbf{A} = \mathbf{A} \parallel \mathbf{B} + \frac{\mathbf{A} \cdot \mathbf{B}}{\left \| \mathbf{B} \right \|^{2}}\mathbf{B}\) \(\mathbf{A} \parallel \mathbf{B} = \mathbf{A} - \frac{\mathbf{A} \cdot \mathbf{B}}{\left \| \mathbf{B} \right \|^{2}}\mathbf{B}\)
이제 우리가 본래 사용했던 기호로 식을 정리해주면:
\[\mathbf{view}_{y} = \mathbf{up} - \frac{\mathbf{up} \cdot \mathbf{view}_{z}}{\left \| \mathbf{view}_{z} \right \|^{2}}\mathbf{view}_{z}\]어차피 $\mathbf{view}_{z}$는 단위 벡터이므로:
\[\mathbf{view}_{y} = \mathbf{up} - \left ( \mathbf{up} \cdot \mathbf{view}_{z}\right ) \mathbf{view}_{z}\]마지막으로 x+축을 구해보자. 사실상 $\mathbf{view}{z}$ 벡터와 $\mathbf{view}{y}$ 벡터가 이루는 평면에 수직인 방향이 곧 x 기저가 아니겠는가?
\[\mathbf{view}_{x} = \frac{ \mathbf{view}_{z} \times \mathbf{view}_{y} }{\left \| \mathbf{view}_{z} \times \mathbf{view}_{y} \right \|}\]이제 남은 것은 세상 공간의 원점을 카메라의 위치로 옮겨오고, 좌표계 변환만 해주면 된다:
색인
- Coordinate Systems (Direct3D 9). Microsoft Documentation
- Coordinate Systems. LearnOpenGL
- Setting Up a Proper Vulkan Projection Matrix. Johannes Unterguggenberger's Blog
- Projection Transform (Direct3D 9). Microsoft Documentation
- World Transform (Direct3D 9). Microsoft Documentation
- Model View Projection. Jordan Santell's Blog.