컴퓨터 그래픽스 기초: 02 사소한 수학 (2023.05.18)

Home

목차

그래픽스는 결국 수학을 코드로 옮긴 것이므로 수학이 간결해지면 코드도 간결해진다. 여기서 다루는 주제는 튜토리얼의 느낌보다는 참고 자료로서의 성격이 더 강하다.

2.1 집합과 사상mapping

사상은 그냥 함수라 생각하면 된다. 수학에서는 한 타입의 입력변수를 받아 다른 특정 타입의 한 개체에 사상(반환)해준다. 여기서 타입은 곧 집합을 의미한다.

임의의 두 집합 A와 B가 있고, a ∈ A, b ∈ B라 할 때, 이 두 집합의 데카르트 곱cartesian product A × B를 통해 세번째 집합을 만들 수 있다. 이때 이 세번째 집합은 A와 B의 원소의 짝으로 이루어져 (a, b) ∈ A × B를 만족한다. A × A = A²로 표기한다.

• R: 실수
• R⁺: 양의 실수 (0 포함)
• R²: 2D 평면에서의 순서 있는 짝들
• Rⁿ: n차원 데카르트 좌표계의 점들
• Z: 정수
• S²: 단위 구 위의 3차원 점(R³의 점)의 집합

만약 실수를 정수로 사상하는 함수 f가 있다고 하자:

f : R → Z

이때 R을 정의역domain이라 부르고 Z를 타겟target(필자: 공역codomain인 듯?)이라 부른다.

int f(real_t r);

요런 느낌.

이때 어떤 한 정의역의 원소 a에 의해 사상된 f(a)를 상image이라 부른다. 모든 정의역에 의한 상을 치역range이라 부른다.

2.1.1 역사상inverse mapping

역함수inverse function 얘기하는 거다. 역함수가 존재하려면 공역이 곧 치역이어야 하고, 일대일 대응이어야 한다. 이런 함수를 전단사 함수bijection라 부른다.

2.1.2 구간interval

함수의 범위를 제한하는 방법이다. 개구간open interval과 폐구간closed interval이 있다.

개구간 x &in; (0, 1)은 곧 0 < x < 1를 의미하고, 폐구간 x &in; [0, 1]은 0 &leq; x &leq; 1를 의미한다. 둘을 섞어 쓸 수도 있다. x &in; [0, 1)은 0 &leq; x < 1이다.

2.1.3 로그logarithm

고등학교 수학 수준이다.

2.2 이차방정식 풀기

이차방정식quadratic equation은 중학교 수학 수준이다.

2.3 삼각법trigonometry

고등학교 수학 수준이다.

2.3.1 각

각은 고등학교 수학에서도 배우지만, 두 선분의 벌어진 정도로 정의하는 것이 아닌, 단위 원의 호의 길이로 정의된다.

By Gustavb - Own work, Public Domain, Link

이때 이 호의 길이의 단위를 라디안radian이라 부르며, 총합은 원의 둘레인 2π이다.

2.3.2 삼각함수

고등학교 수학 수준이다.

2.3.3 유용한 항등식

• 이동 항등식
  • sin(-A) = -sin A
  • cos(-A) = cos A
  • tan(-A) = -tan A
  • sin(π / 2 - A) = cos A
  • cos(π / 2 - A) = sin A
  • tan(π / 2 - A) = cot A
• 피타고라스 항등식
  • sin² A + cos² A = 1
  • sec² A - tan² A = 1
  • csc² A - cot² A = 1
• 덧셈 뺄셈 항등식
  • sin(A + B) = sin A cos B + sin B cos A
  • sin(A - B) = sin A cos B - sin B cos A
  • sin(2A) = 2 sin A cos A
  • cos(A + B) = cos A cos B - sin A sin B
  • cos(A - B) = cos A cos B + sin A sin B
  • cos(2A) = cos² A - sin² A
  • tan(A + B) = (tan A + tan B) / (1 - tan A tan B)
  • tan(A - B) = (tan A - tan B) / (1 + tan A tan B)
  • tan(2A) = 2 tan A / (1 - tan² A)
• 반각 항등식
  • sin²(A/2) = (1 - cos A) / 2
  • cos²(A/2) = (1 + cos A) / 2
• 곱셈 항등식
  • sin A sin B = -(cos(A + B) - cos(A - B)) / 2
  • sin A cos B = -(sin(A + B) - sin(A - B)) / 2
  • cos A cos B = -(cos(A + B) + cos(A - B)) / 2
• 삼각형 항등식
  • 사인 법칙
    • LawOfSines
  • 코사인 법칙
    • LawOfCosines
  • 탄젠트 법칙
    • LawOfTangents

2.3.4 입체각solid angle과 구면삼각법spherical trigonometry

이차원에서의 삼각형과는 다르게 구면삼각법에서의 삼각형은 단위 구 위에 정의된 구면 삼각형spherical triangle을 의미한다.

이차원에서 각도를 호로 정의했듯이, 마찬가지로 삼차원에서의 각도인 입체각은 단위 구의 특정 면에 대하여 정의가 된다.

By Andy Anderson - Own work, CC BY-SA 4.0, Link

이차원 각도가 라디안이었다면, 삼차원 각도는 스테라디안steradian이고, 총합은 단위 구의 면적인 4π이다.

2.4 벡터

고등학교 수학이다.

벡터vector란 방향과 길이를 의미한다. 단위 벡터unit vector란 길이가 1인 벡터이다. 영벡터zero vector는 길이가 0인 벡터이며, 이때 방향은 정의되지 않는다.

벡터를 쓸 수 있는 곳들:

• 오프셋offset 혹은 변위displacement
• 위치location/position 혹은 점point (원점origin)

2.4.1 벡터 연산

• 덧셈
  • 평행사변형 법칙
  • 교환 법칙
• 곱셈
  • 스칼라 곱셈
  • 내적
  • 외적

2.4.2 벡터의 데카르트 좌표

고등~대학교 수학.

이차원에서의 한 벡터는 서로 평행하지 않은 두 벡터를 x, y처럼 축으로 삼아 좌표로서 표현할 수 있다. 이때 축으로 사용한 이 두 벡터를 서로 선형 독립성linear independence을 갖는다고 하며, 기저 벡터basis vector라 부른다. x, y 축처럼 서로 직교orthogonal하는 기저가 특히 유용하다. 특히 이 서로 직교하는 기저 벡터가 단위 벡터라면 이를 정규 직교계orthonormal이라 부른다. 이렇듯 두 축의 선형 결합으로 좌표를 표현하는 방식을 데카르트 좌표계라 부른다.

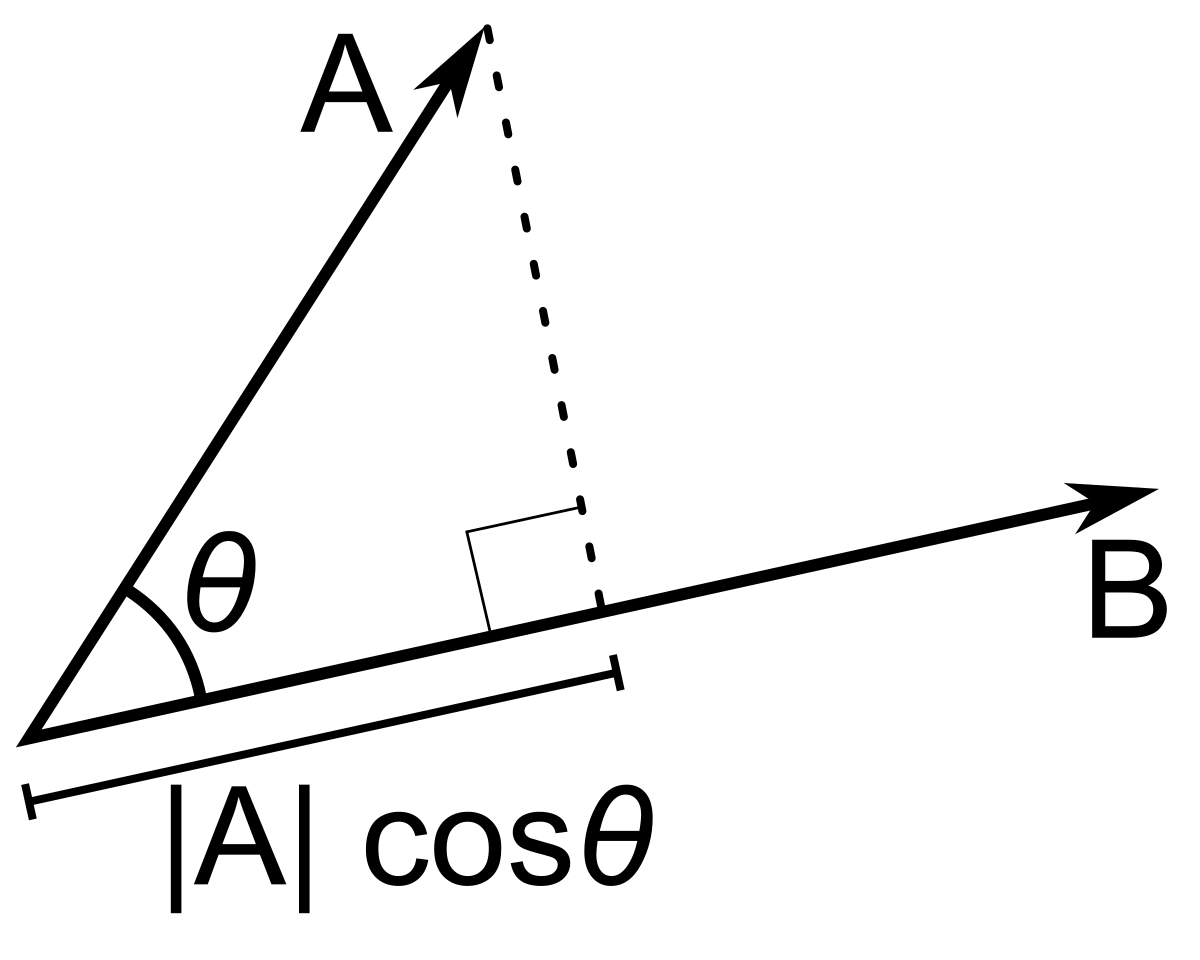
2.4.3 내적

결합 및 교환 법칙이 성립한다.

사영projection할 때 사용해줄 수 있다.

By No machine-readable author provided. Mazin07 assumed (based on copyright claims). - No machine-readable source provided. Own work assumed (based on copyright claims)., Public Domain, Link

2.4.4 외적

보통 3차원에서만 사용한다.

By User:Acdx - Self-made, based on Image:Crossproduct.png, Public Domain, Link

By User:Acdx - Self-made, based on Image:Cross_parallelogram.png, Public Domain, Link

x 축을 오른쪽, y 축을 앞이라고 했을 때 x × y = z인 z 축은 자연스레 하늘, 즉 위를 향하게 된다. 이런 좌표계를 오른손right-handed 좌표계라 부르며 우수右手법이라고도 부른다.

By Acdx - Self-made, based on Image:Right_hand_cross_product.png, CC BY-SA 3.0, Link

2.4.5 정규 직교 기저와 좌표 프레임

좌표계 관리는 그래픽스 시스템의 가장 핵심적인 임무 중 하나다. 특히나 이 임무의 핵심은 정규 직교 기저orthonormal bases의 관리이다.

우리가 보통 알고 있는 우수법의 x, y, z 축을 갖고 원점이 (0, 0, 0)인 좌표계를 전역 좌표계global coordinate라 부른다.

이와는 달리 명시적으로 u, v, w라는 정규 직교 기저와 원점 p를 정의해준다면(즉, 따로 메모리에 저장해줘야함) 이 좌표계는 기준틀frame of reference 혹은 좌표계 프레임coordinate frame이라 부른다. 예를 들어 FPS 게임의 경우 현재 플레이어의 위치를 기준으로 하는 기준틀이 필요할 수도 있을 것이다.

위의 예제처럼 어떤 오브젝트에 대한 좌표계를 지역 좌표계local coordinate system라 부른다.

2.4.6 벡터 한 개로 기저 구축하기

어떤 한 벡터 a가 주어졌을 때, a와 평행한 w를 갖는 정규 직교 기저 u, v, w를 구해야 할 수도 있다.

• w = a /

  a

• u = (t × w) /

  t × w

  (t는 w와 평행하지 않은 임의의 공선collinear 벡터)

• v = w × u

2.4.6 벡터 두 개로 기저 구축하기

만약 두 벡터 a와 b가 직교한다면 두 벡터의 외적 u = b × a(우수법. 좌수법의 경우 a × b)을 나머지 한 기저로 사용하면 된다.

• w = a /

  a

• u = (b × w) /

  b × w

  (t는 w와 평행하지 않은 임의의 공선collinear 벡터)

• v = w × u

2.4.7 기저 유효화하기

컴퓨터 내부 연산이나 저장된 정밀도 때문에 기저가 실제로 정규 직교하지 않을 수도 있다. 이런 경우 때문에 위와 같이 벡터 한두 개로 기저를 구축하는 법을 배운 것이다. 근데 이렇게 되면 초기에 기준으로 삼을 그 기저 외의 새롭게 만들어진 기저는 실제 기저에 비하면 약간의 오류가 생긴다. 나중에 SVD를 활용해 더 나은 방법으로 기저를 구할 것이다.

2.5 적분

고등학교 수학.

2.5.1 평균과 가중 평균weighted average

공간을 적분한 걸 넓이를 적분한 걸로 나누면 평균을 얻을 수 있다.

예를 들어 어떤 한 나라 country의 2D height map elevation()이 있다고 가정해보자. 이 map의 지형의 부피 volume은 곧 integrate(elevation(), country)이고, 그 넓이는 integrate(1, country)가 된다. 그러면 평균 elevation은 volume / area이다.

만약 가중치를 두어 평균을 구하고 싶다면, 적분 함수에 곱해주면 된다. 가중치 평균 = integrate(elevation() * temperature(), country) / integrate(temperature(), country).

2.5.2 입체각 적분

float shade = integrate(cos()*f*(), unit-hemisphere)
float weightedShade = integrate((1/pi)*cos()*f*(), unit-hemisphere) // integrate(cos(), unit-hemisphere) = pi

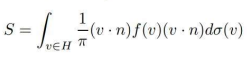
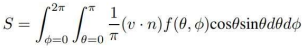
2.6 밀도 함수density function

고등학교 확통 수학.

대학교에서도 배우긴 함.

2.7 곡선curve과 곡면surface

2.7.1 2D 암시 곡선implicit curve

곡선을 표현하는 방법에는 이 곡선이 그릴 함수를 정의하는 암시적인 방정식implicit equation f(x, y) = 0을 사용하는 방법이 있다.

2.7.2 2D 기울기

만약 f(x, y)라는 함수가 위에서 언급한 height map이라고 한다면, f(x, y)의 기울기gradient 벡터는 더 높은 곳을 바라보는 방향을 가리킨다.

변수가 2개 이상일 때, 한 변수를 고르고, 나머지를 변수들은 상수 취급하여, 고른 한 변수로 다변수 함수를 미분하는 것을 편미분partial derivative이라 부른다.

2.7.3 3D 암시 곡면implicit surface

2D 암시 곡선에서 차원 하나 추가한 것이다.

f(x, y, z) = f(p) = 0

2.7.4 암시 곡면의 곡면 법선surface normal

점의 기울기를 구하여