게임공학 공부 노트 (2022.06.03)

1. Inverse Kinematics 입문

개요

FK: 연속된 관절과, 각 관절에 대한 각도가 주어졌을 때, 관절의 끝지점의 위치를 결정하는 문제.

연속된 관절들을 kinematics chain이라 부름. 어깨가 움직이면 팔꿈치가 움직이듯, chain처럼 움직인다는 것임.

FK의 문제는, kinematics chain의 마지막 뼈 끝부분의 위치를 모른다는 것. 반대로 IK는 그 위치를 안다는 것임.

결국 IK는 어떤 kinematics chain이 주어지고, 목표 위치 target이 주어졌을 때, 마지막 뼈 끝부분, 즉 end effector의 위치를 target으로 보내는 문제를 해결하는 문제임. 당연히 이 방법에는 해가 없을 수도, 해가 하나만 있을 수도, 여러 가지 해가 있을 수도 있음. 해가 여러 개면, 여러 다양한 방법꼼수으로 구하면 됨.

IK 문제 푸는 법

두 가지 방법이 있음: 해석학적 방법, 수치적 방법.

해석학적 방법
- 직접 해결할 수 있는 방정식이 존재함.
- 문제 풀이가 빠르고, 가장 선호하는 방법임.
- 연결고리가 얼마 없는 경우에는 거의 안 쓺.
수치적 방법
- 해는 아니고, 거의 해에 가까운 답을 찾는 방법.
- 주로 사용하는 방법:
  - 여러 번 반복하여 해에 점근하는 방법.
  - 더 작은 문제들로 나누어 푸는 방법.
- 해석학적 방법보다는 비쌈.
- 대표적인 방법:
  - Cyclic Coordinate Decent (CCD)
    - 각 연결고리를 독립적으로 바라봄.
    - 잎 노드(end effector)에서부터 차례대로 부모로 올라가는데, 이때 end effector과 target 간의 오류를 최소화하려고 함.
    - 적당히 괜찮은 결과가 나올 때까지 몇 번만 처리하면 됨.
    - 해가 좀 비현실적일 수도 있음.
      - 잎 노드부터 보니까 막 손목이 엄청 과도하게 꺾여있거나 그럴 수도 있음.
  - Jacobian Matrix
    - 전체 IK chain에 대해 처리함
    - 행렬의 각 열이 곧 각 연결고리가 회전할 때 end effector가 어떻게 변하느냐(선형 근사)에 대한 것임.
    - 정답 구하는 게 느린데, CCD보다는 일반적으로 더 괜찮은 결과가 나옴.

Grassman 대수

Exterior product 혹은 wedge product.

R³의 두 벡터의 wedge product의 결과는 벡터가 아닌, bivector라는 새로운 존재임.

By User:Acdx - Self-made, based on Image:Cross_parallelogram.png, Public Domain, Link

Cross product를 할 때 보통 두 벡터 a와 b가 평행사변형을 만드는데, 이게 곧 a와 b의 wedge product의 결과로 나온 bivector라고 생각하면 됨. 벡터와 bivector의 wedge product는 trivector가 생김.

이렇듯 스칼라, 벡터, bivector, trivector과 wedge 연산자에 대한 대수를 R³에 대한 그라스만 대수라 부름.

그라스만 대수 참고

Wedge Product

a와 b의 wedge product는 a ∧ b로 표현. “a wedge b”라고 읽음.

s ∧ t = t ∧ s = st
s ∧ v = v ∧ s = sv
v ∧ v = 0

교환 법칙이 반대로 됨.

a ∧ b = -b ∧ a

Bivector

두 벡터가 기저를 이루는 2D 영역을 의미함.

By Brews ohare - Own work, CC BY-SA 3.0, Link

위의 그림에서처럼 a ∧ b인지, b ∧ a인지에 따라 방향이 달라짐.

Bivector을 삼차원 벡터로 표기할 수 있음.

세 개의 기저 벡터 e₁, e₂, e₃가 있을 때, 어떤 삼차원에서의 벡터 a = a₁e₁ + a₂e₂ + a₃e₃

이때

a ∧ b = (a₁b₂ - a₃b₂)(e₂ ∧ e₃) + (a₃b₁ - a₁b₃)(e₃ ∧ e₁) + (a₁b₂ - a₂b₁)(e₁ ∧ e₂)

즉, wedge product의 결과로 세 bivector 기저 e₂ ∧ e₃, e₃ ∧ e₁, e₁ ∧ e₂가 생김. 이걸 기저 bivector라 부름.

앞으로:

e₁₂ = e₁ ∧ e₂ e₂₃ = e₂ ∧ e₃ e₃₁ = e₃ ∧ e₁ e₁₂₃ = e₁ ∧ e₂ ∧ e₃

$3dBivector$

결합 법칙 안 됨.

Trivector:

Trivector

a ∧ b ∧ c = (a₁b₂c₃ + a₂b₃c₁ + a₃b₁c₂ - a₁b₃c₂ - a₂b₁c₃ - a₃b₂c₁)(e₁ ∧ e₂ ∧ e₃)

크기는 det([a b c]).

기저가 하나 밖에 없으니 마치 스칼라 같다고 해서 유사스칼라pseudoscalar라고 부름.

사원수. 쿼터니언.

3D 그래픽스에서 회전을 표현할 때 사용하는 수.

쿼터니언의 장점:

저장 공간 적음
쿼터니언 합치는데 필요한 산술 연산 횟수가 더 적음
부드러운 애니메이션을 만드는데 더 보간이 잘 됨.

사원수학

사원수 집합은 사차원 벡터 공간이고, 이 집합에 속한 원소 q = < w, x, y, z > = w + xi + yj + zk.

보통 q = s + v라 표현하는데, 여기서 s는 q의 w 성분, 즉 스칼라 성분을 의미하고, v는 x, y, z 성분을 의미하는 벡터 성분을 의미.

i, j, k는 허수 개념의 확장.

i² = j² = k² = -1
ij = -ji = k
jk = -kj = i
ki = -ik = j

교환 법칙 X. 그래서 올바른 순서로 곱해야함.

q₁q₂ = (w₁w₂ - x₁x₂ - y₁y₂ - z₁z₂) + (w₁x₂ + x₁w₂ + y₁z₂ - z₁y₂)i + (w₁y₂ - x₁z₂ + y₁w₂ + z₁x₂)j + (w₁z₂ + x₁y₂ - y₁x₂ + z₁w₂)k

즉,

q₁q₂ = s₁s₂ - v₁·v₂ + s₁v₂ + s₂v₁ + v₁×v₂임.

이때 둘 다 스칼라 성분이 0이면,

q₁q₂ = -v₁·v₂ + v₁×v₂ = -q₁·q₂ + q₁×q₂임.

사원수로 회전하기

삼차원에서의 회전은 어떤 삼차원 공간 R³을 다시 자기 자신에 매핑하는 어떤 함수 φ라 생각하면 됨. φ가 회전이 되려면, 길이, 각도, 왼손/오른손 기준을 유지해야함.

||φ(P)|| = ||P||를 만족하면 길이는 보존됨.

φ(P₁)·φ(P₂) = P₁·P₂를 만족하면 각도도 보존됨.

φ(P₁)×φ(P₂) = φ(P₁×P₂)를 만족하면 손 기준도 보존됨.

이때 P가 스칼라 성분이 0인 사원수라고 가정하면 P₁P₂ = -P₁·P₂ + P₁×P₂이니까, 결국 마지막 두 조건은 φ(P₁)φ(P₂) = P₁P₂로 표현 가능함.

이때 위의 방정식 φ(P₁)φ(P₂) = P₁P₂을 만족하는 함수 φ를 homomorphism이라 부름.

이때 이 함수는

φ_q(P) = qPq^-1의 형태를 띰.

이 식은 위의 모든 조건을 만족함. 이때 사원수 q는 축 A에 대하여 θ 만큼의 회전으로 대응해줘야함. 일단 여기서는 간단하게 문제를 보기 위해 q = s + v를 단위 사원수라고 가정함.

qPq^-1 = s²P + 2sv×P + (v·P)v - v×P×v = (s² - v²)P + 2sv×P + 2(v·P)v.

여기서 v = tA라고 가정. A는 단위 벡터.

qPq^-1 = (s² - v²)P + 2stA×P + 2t²(A·P)A.

임의의 축 A에 대해 벡터 P를 회전시키는 식:

P^’ = Pcosθ + (A×P)sinθ + A(A·P)(1 - cosθ).

이 식과 위의 qPq^-1를 비교해서 보면:

s² - t² = cosθ 2st = sinθ 2t² = 1 - cosθ

즉, t = sin(θ/2), s = cos(θ/2).

결국 단위 사원수 q = cos(θ/2) + Asin(θ/2)임.

이제 이걸 변환 행렬로 만들어주면

$p$

$q$

$prp$

$QuaternionRotationMatrix$

기하곱

ab = a · b + a ∧ b

즉, ab는 스칼라 성분과 bivector 성분 둘을 갖고 있음. bivector 자체는 a와 b가 이루는 모양에 대한 정보는 없음. 하지만 a · b에 있는 코사인 정보 덕에 기하곱을 통해 a와 b가 이루는 각을 알 수 있게 됨. 즉, G = ab는 단순 bivector를 확실하게 우리가 생각할 수 있는 평행사면형으로 만들어주는 것임. 물론 그 평행사변형을 구성하는 벡터의 크기나 순서는 G만 봐선 알 수 없지만, b 하나만 구해도 a를 구할 수 있음.

기하곱에서의 역원:

v^-1 = v / v²

이걸로 벡터 나눗셈을 구할 수 있음:

a / b = ab^-1

이러면 반드시 a = cb가 될 것임. 이때 c는 어떤 벡터임.

이러면 a = (a/b)b = (ab/b²)b = ((a · b) / b²)b + ((a ∧ b) / b²)b

여기서 첫번째 성분은 a를 b에 사영하는 식과 같으므로 두번째 성분은 rejection의 역할을 해야 함.

By Paolo.dL - Own work, CC BY-SA 3.0, Link

a를 b에 사영한 것이 a₁, a에서 b로 reject한 것이 a₂

즉, a_||b = (a · b) / b, a_⊥b = (a ∧ b) / b.

G/b의 결과는 결국 G = ab를 만족하는 b와 함께 정확한 크기와 각도를 갖는 a 벡터임.

만약 G = av일 때 G / v는 a인데, G / a는?

G / a = v’라고 가정하면, v’a = G임.

이때, av = v’a이므로, v’ = ava^-1임.

즉, v’ = ((a · v) / a) + ((a ∧ v) / a) = ((v · a) / a) - ((v ∧ a) / a) = v_||a - v_⊥a가 됨.

이 식은 결국 a 벡터에 대한 반사와 같음. 결국 a에 대해 180도 회전한 식이 됨.

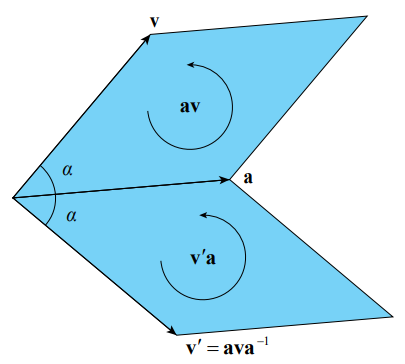
VectorDivision

이때 v’를 또다른 벡터 b에 대해서도 회전을 해주면 v’‘를 구할 수 있음.

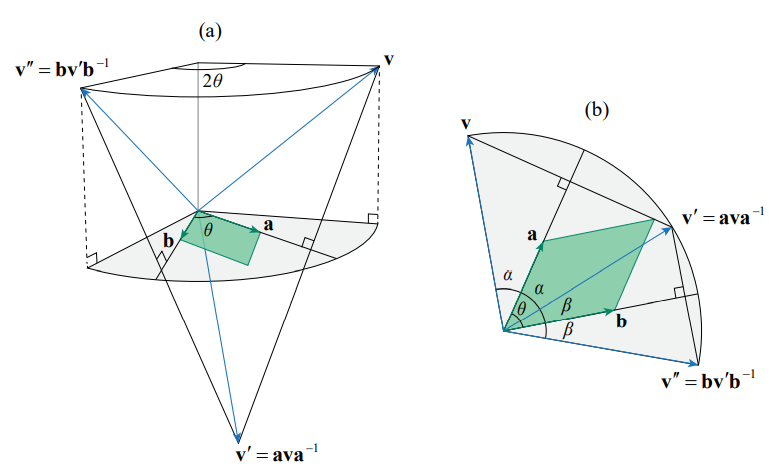
Rotor

위와 같은 그림이 되는 것임. 결국 v’‘ = bv’b^-1 = bava^-1b^-1이 됨. 이때 R = ab로 두면 v’‘ = RvR^-1이 됨.

여기서 R의 bivector는 위의 그림에서처럼 a와 b가 만드는 평면에 속함.

결론적으로 v는 a × b 벡터에 대해서 2θ 만큼 회전을 한 것임.

이때 R = ba를 rotor라고 부름. 여기서 2θ라는 각도는 a에서 b 방향, 즉 bivector b ∧ a의 방향과 평행함. 그래서 보통 R = a · b - a ∧ b.

3차원에서 a ∧ b는 a × b라는 회전축의 complement라고 생각할 수 있음. 여기서 complement라는 것은, x축의 complement는 y축과 z축의 bivector인 것. 이때 표기를

Complement

와 같이 표기함

즉, a와 b가 단위 벡터라면, R = cosθ - (sinθ) n^-

여기서 n은 a × b와 같은 방향을 가리키는 단위 벡터임. 이건 2θ만큼 회전하는 것이니, θ만큼 회전하려면:

R = cos(θ/2) - (sin(θ/2)) n^-

2. IK의 수치적 해법

각속도

아래 그림에서처럼 질량이 m인 어떤 한 입자를 단위 벡터 A에 길이가 r인 줄로 연결했다고 가정.

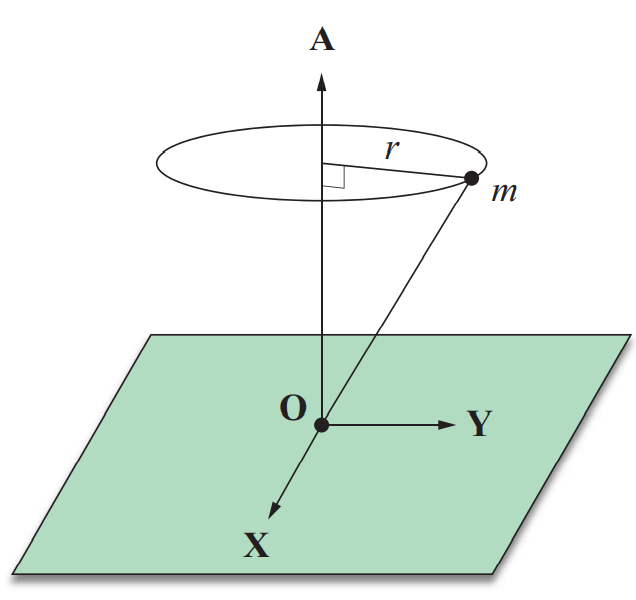
AngularVelocityFigure

이때 오른손 좌표계라고 할 때(X × Y = A) θ(t)가 입자를 매단 줄을 XY 평면에 사영한 벡터가 시간 t 때 반시계 방향으로 X 축과 이루는 각도라고 가정. 이때 이 입자의 각속도는 각도의 변화량이며, 보통 ω로 표기함:

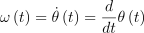
AngularVelocityEquation

각속도는 보통 회전축 A에 평행하면서 크기가 |ω(t)|인 벡터로 표기함. 즉 각속도 벡터 ω*(t)는 다음과 같음:

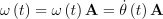
AngularVelocityVectorEquation

회전하는 이 입자가 공간에서 이동하는 속력 v(t)는 이 입자의 각속도와 이 입자와 회전축 간의 길이 간의 곱으로 구할 수 있음:

v(t) = |ω(t) r|

여기서 방향 정보를 추가한다고 가정. 벡터 함수 r(t)이 회전축을 기준으로 한 상대 위치라고 가정할 때, 선형 속도 벡터 v(t)는 다음과 같음:

v(t) = ω(t) × r(t)

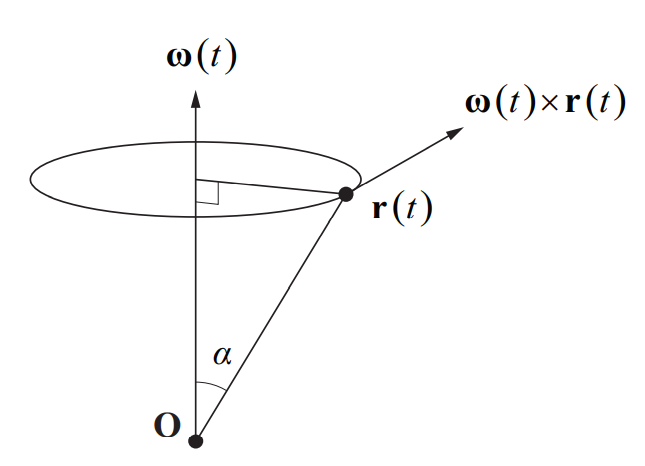
LinearVelocityFigure

이때 선형 속도는 각속도와 직각을 이룸.

By Krishnavedala - Own work, CC0, Link

만약 이 입자가 선형 속도 v만큼 이동할 때의 각속도는 결국 v의 수직 성분 v_⊥에 대해서 구할 수 있음. v(t) = ω(t) r 이므로

v_⊥ = ω(t) × r
ω(t) = v_⊥ / r
ω(t) = (v sin(θ)) / r

이건 2D에서의 얘기이므로, 벡터로 확장하면,

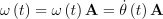
AngularVelocityVectorEquation

이므로,

ω(t) = ω(t) A = ((|v| sin(θ)) / r) A
ω(t) = ((r |v| sin(θ A)) / (r r))
ω(t) = ((r × v) / r²)

a × b = |a||b|sin(θ)n이기 때문 ^_^

야코비 방법

해석학적인 방법으로 IK를 해결하기엔 요즘 애니메이션들은 좀 복잡한 편임. 이 경우엔 매 프레임마다 지속적으로 목표 지점까지 다다르도록 각 관절의 각도를 변화시켜주는 것임. 여러 방법이 있지만 가장 대중적인 방법이 바로 야코비Jacobian 방법임. 야코비 방법은 야코비 행렬을 사용하는 방법으로, 이 행렬은 편미분으로 구성된 행렬을 의미함.

수학적으로 보자면, 만약 임의의 여섯 가지 함수가 존재하고, 여섯 가지의 서로 독립적인 변수들 x_i가 있을 때, 그 결과인 y_i = f_i(x_i)이 있을 것임.

이때 각 결과값의 변화량을 각 입력값의 변화량으로 표현할 수 있음:

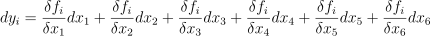
DifferentialsOfYi

위의 식을 벡터에 대해서 표현할 수 있음:

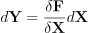
VectorDifferentialsOfY

이때 이 X에 대한 F의 편미분으로 구성된 행렬을 야코비라 부르며, 현재 x_i 값들에 대한 함수라고 보면 됨. 마치 X의 속도를 정의역으로, Y의 속도를 치역으로 갖는 함수라고 생각하면 됨:

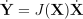
JacobianMapping

어떤 시점에서 야코비는 결국 x_i에 대한 함수임. 그 다음 시점에서는 X가 바뀌기에 야코비로 그 변환을 표현해줄 수 있음. 즉, x_i는 각 관절의 값이 되며, y_i는 end effector의 위치와 orientation이 됨.

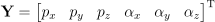
EndEffectorY

이런 식으로 표현할 수도 있는 것임.

IK의 경우 야코비는 곧 관절의 각속도 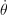AngularVelocity 를 end effector의 위치와 orientation EndEffectorPositionOrientation 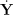이 됨. 즉,

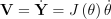
JacobianEndEffector

여기서 V는 선형 및 회전 속도로 구성된 벡터이므로, end effector의 희망 변화량을 의미하게 됨. 이 희망 변화량은 현재 위치/orientation과 목표 간의 차이에 기반하여 구하게 될 것임.

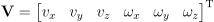
VelocityVector

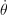AngularVelocity 는 각 관절의 속도, 혹은 각 관절의 변화량을 의미함. 이게 결국 구해야하는 값임:

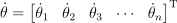
AngularVelocitiesVector

야코비 행렬 J는 결국 뒤의 둘 사이의 관계를 의미하며, 현재 pose에 대한 함수임. 이 행렬은 다음과 같이 생겼을 것임:

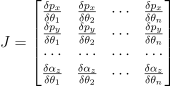
JacobianMatrix

야코비 행렬의 각 항은 결국 특정 관절이 특정 end effector에게 주는 변화량을 의미함. 예를 들어 팔꿈치 관절이라면 end effector에 대한 회전 변화량 ω은 그저 해당 관절에서의 회전축에 대한 속도를 의미할 뿐임. 회전 관절의 경우 end effector의 선형 변화량은 곧 관절의 회전축과, 해당 관절에서 end effector까지를 잇는 벡터의 외적과 같음. 회전 관절에서의 회전은 곧 즉각적으로 end effector의 선형 움직임이 됨.

목표 각속도 및 선형 속도는 현재 end effector의 설정 값과 목표 설정 값 간의 차를 바탕으로 구하는 것임. end effector의 각속도와 선형 속도를 각 관절의 회전으로 구하는 방법:

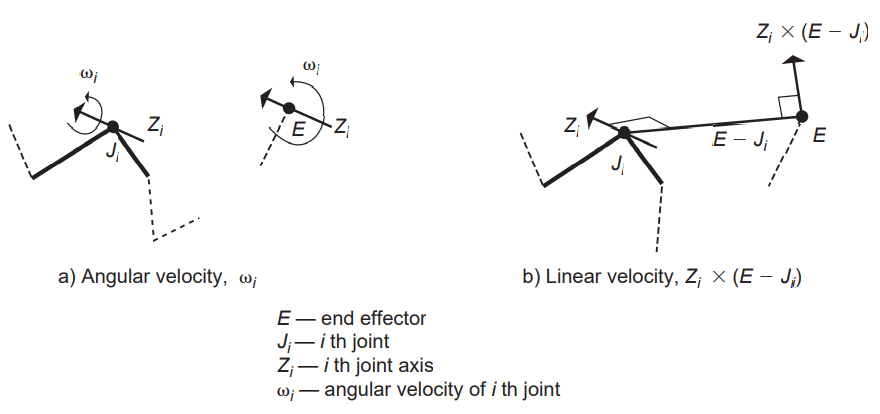
AngularLinearVelocities

여기서 문제는 end effector의 목표 속도를 가장 잘 맞추는 일차 결합을 구하는 것임. 야코비는 이 문제를 행렬의 형태로 처리하려는 것임.

참고로 이때 야코비 행렬을 만들 때, 각 관절의 좌표계가 동일해야한다는 것임.

예를 들어 검지처럼 한 방향으로만 회전이 가능한 관절이 세 개인 경우,

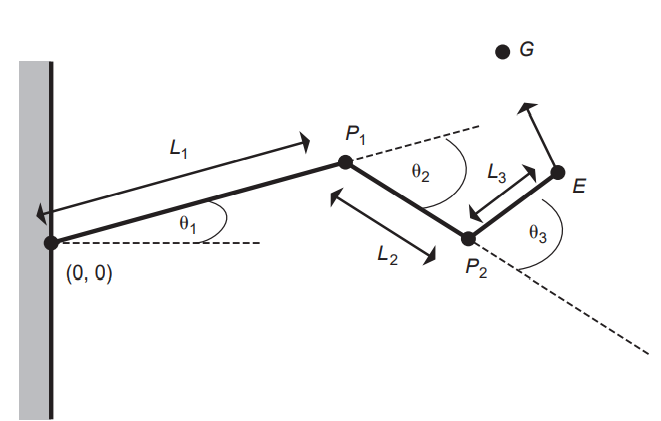
PlanarThreeJointManipulator

end effector인 E를 목표 G로 옮겨야 함. 각 관절의 회전축은 현재 그림과 수직임. 각 관절마다의 회전을 적용한 결과 벡터 g_i는 각 관절의 회전축와 각 관절에서 end effector까지를 가리키는 벡터 V_i의 외적으로 구할 수 있으며, 이것이 야코비 행렬의 열을 결정하게 됨. 이때 g_i의 크기는 관절과 end effector 간의 거리를 의미하는 함수가 됨.

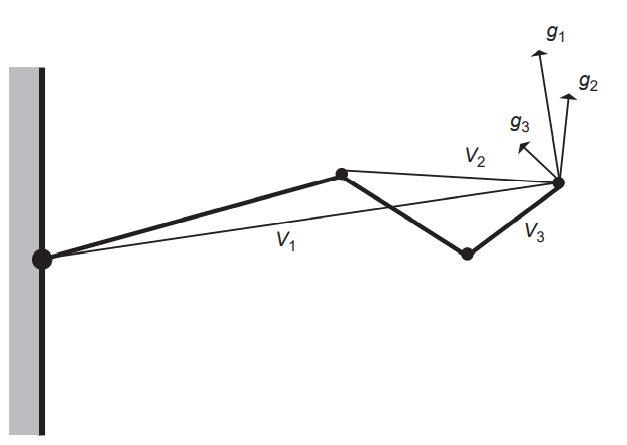
ChangesInPosition

end effector에 가할 목표 변화량은 end effector의 현재 위치와 목표 위치 간의 차임 (선형 변화량. 선형 속도):

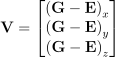
DesiredChange

이제 목표 변화량을 값으로 표현한 벡터를 야코비 행렬 곱하기 관절 변화량으로 두면 됨:

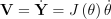
JacobianEndEffector

선형 속도: Z_i × (E - J_i)

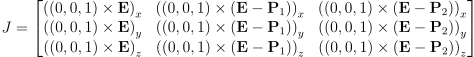
JointAngleChangesJacobian

야코비 역행렬

야코비를 이제 구했으면

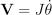
JointAngleVelocities

이 식을 해결해야함. 만약 J가 사각행렬이라면 역행렬 J^{-1을 구해서 end effector의 속도가 주어졌을 때 각 관절의 각속도를 구할 수 있음.}

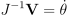
JacobianInverse

근데 만약 역행렬이 존재하지 않는다면 현재 system은 주어진 관절 각도에 대해 singular 상태라고 함. 특이성은 관절의 속도의 일차 결합이 희망 end effector 속도를 낼 수 없을 때 발생함. 예를 들어 완전히 손가락을 쭉 편 상태에서, target 위치가 손가락 끝마디나 중간마디 중간 어딘가에 있을 때에 특이성이 발생함. 이 경우 각 관절 각도의 변화량 g는 언제나 목표 방향과 수직일 것임. 그러므로 어떻게 결합을 하든 목표 방향 벡터를 만들 수가 없음. 근데 이건 우리가 시각적으로 보이니까 특이성이 발생하는 걸 알지, 이게 언제나 그렇게 판단할 수는 없는 것임.

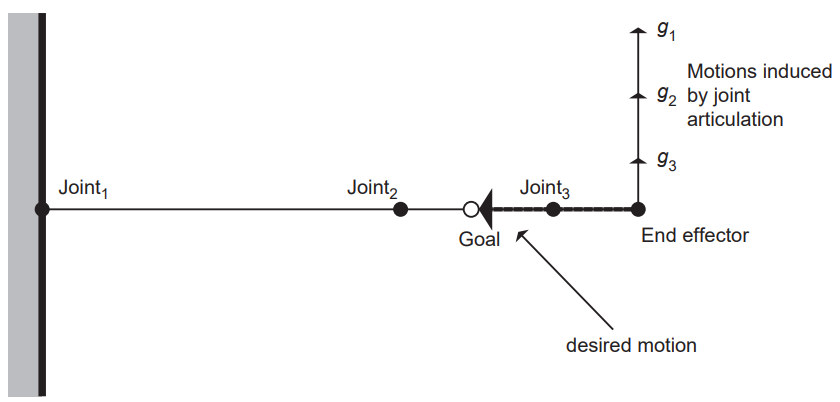
SingularConfiguation

이게 단순히 특이성이 아니라고 해서 문제가 없는 건 아님. 만약 위의 예시에서 약간은 수직이 아니라고 해도, 저 g들 갖고 desired motion vector 만들려면 값이 엄청 커짐. 이러면 특이성 근처의 상황에서는 막 확 확 바뀌게 됨. 이건 좀 더 그럴 듯한 값으로 좀 clamping을 해줘야 함. 그렇게 해도 수치적 오류에 의해 예측하기 어려운 움직임을 낼 수도 있음.

특이성의 문제를 줄이려면 manipulator가 반복적이면 됨. 즉, 만족할 제한사항보다 더 많은 DOF가 있으면 됨. 이러면 야코비가 사각 행렬이 아니고, IK 문제에 대해 여러 가지, 무한한 해가 존재할 수도 있음. 야코비 행렬이 사각 행렬이 아니므로 전통적인 역행렬이 존재하지 않음. 하지만 만약 J의 열들이 일차 독립적이라면(즉, J가 full column rank를 갖는다면) (J^TJ)^-1이 존재하므로, 유사역원pseudoinverse J^{+로 J^{+ 사용. 이게 가능한 이유가, 어떤 행렬을 자신의 전치행렬과 곱하면 그 결과는 무조건 사각행렬이기 때문에 역행렬이 존재할 수도 있음:}}

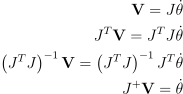
PseudoInverse

J의 행들은 일차 독립적이므로 JJ^T은 invertible이며, 유사역행렬은 J⁺ = J^T(JJ^T)^-1이 됨. 유사역행렬은 end effector의 목표 속도를 필요한 관절의 각도 변화량으로 매핑해주는 함수임. 이를 통해 역행렬을 대체하면 됨:

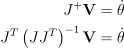
PseudoInverseMapping

이제 위의 식에서 약간의 수정을 해준 다음, LU 분해를 통해 β에 대한 아래 방정식을 풀 수 있게 됨:

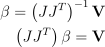
LUDecomposedPseudoInverse

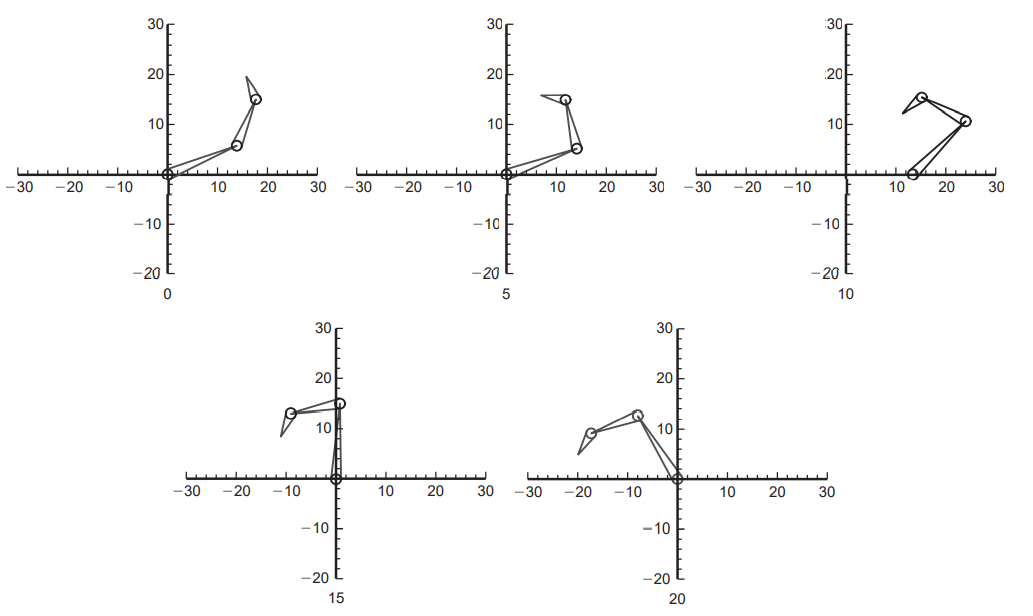
이걸 이제 아래 식으로 수정해서 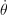AngularVelocity 를 구할 수 있음:

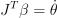
SubstitutedVelocities

이때 단순 오일러 방법으로 관절의 각도를 업데이트해줘도 됨. 참고로 매 프레임마다 야코비 행렬을 새로 구해야줘야 함. 이건 end effector가 목표에 적당한 범위 내에 도달할 때까지 반복하는 것임.

참고로 이게 매 프레임마다 처리되는거다보니까 프레임이 너무 크면, 확 확 확 바뀌어서 오히려 target으로 잘 못 갈 수도 있음. 그래서 차라리 의도적으로 업데이트 주기를 줄이는게 나을 수도 있음.

IK2dExample

예를 들어 위에서처럼 검지를 2차원에 맵핑한 예시를 들어봅시다. 이때 각각 길이가 15, 10, 5고, 초기 각도가 π/8, π/4, π/4라고 하고, 목표 위치가 ( -20, 5 )라고 가정. 이러면 end effector가 목표까지 가는데 21 개의 프레임이 생성이 됨. 위의 그림은 0번째, 5번째, 10번째, 15번째, 20번째 프레임을 보여주는 것임. end effector만 보면 거의 직선으로 움직였다는 것을 알 수 있음.

근데 제한을 준 경우에도 특이성 문제가 발생할 수 있음. 이걸 해결하려는 한 방법 중 하나가 damped least-squares approach임:

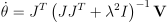
DampedLeastSquaresApproach

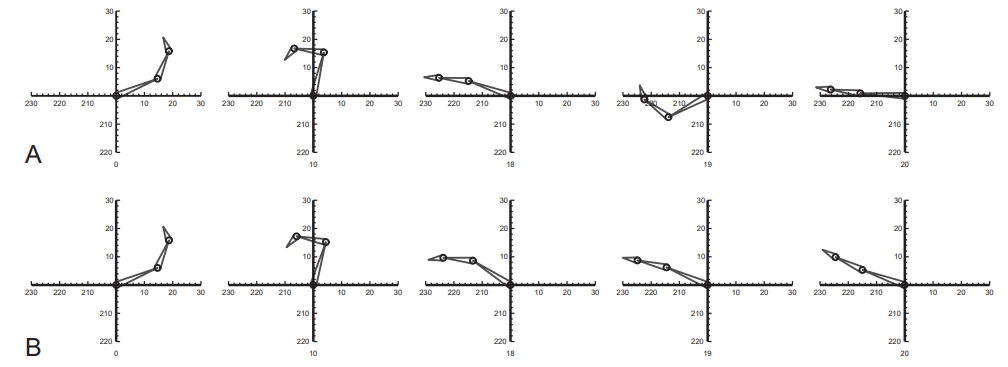
이 방정식이 원래 방정식에 비해서 특이성에 근접한 범위에선 더 잘 되긴 함. 대신 해로 수렴하는 데에 지불하는 비용이 조금 더 커질 뿐임. 아래 그림에서처럼 A가 야코비, B가 DLS일 때의 차이점을 보여줌. 이때 target이 손가락의 범위를 벗어나있는 ( -35, 5 )인데, 이 경우 DLS를 썻을 때가 더 좋은 결과를 보여줌.

PseudoInverseVsDampedLeastSquares

4. IK에서의 뉴턴 방법

뉴턴 방법

원문은 뉴턴-랩슨 방법이지만, 간단히 그냥 뉴턴 방법이라 부름. 그냥 어떤 임의의 연속 함수가 주어졌을 때, 그 해를 찾는 반복적인 방법임.

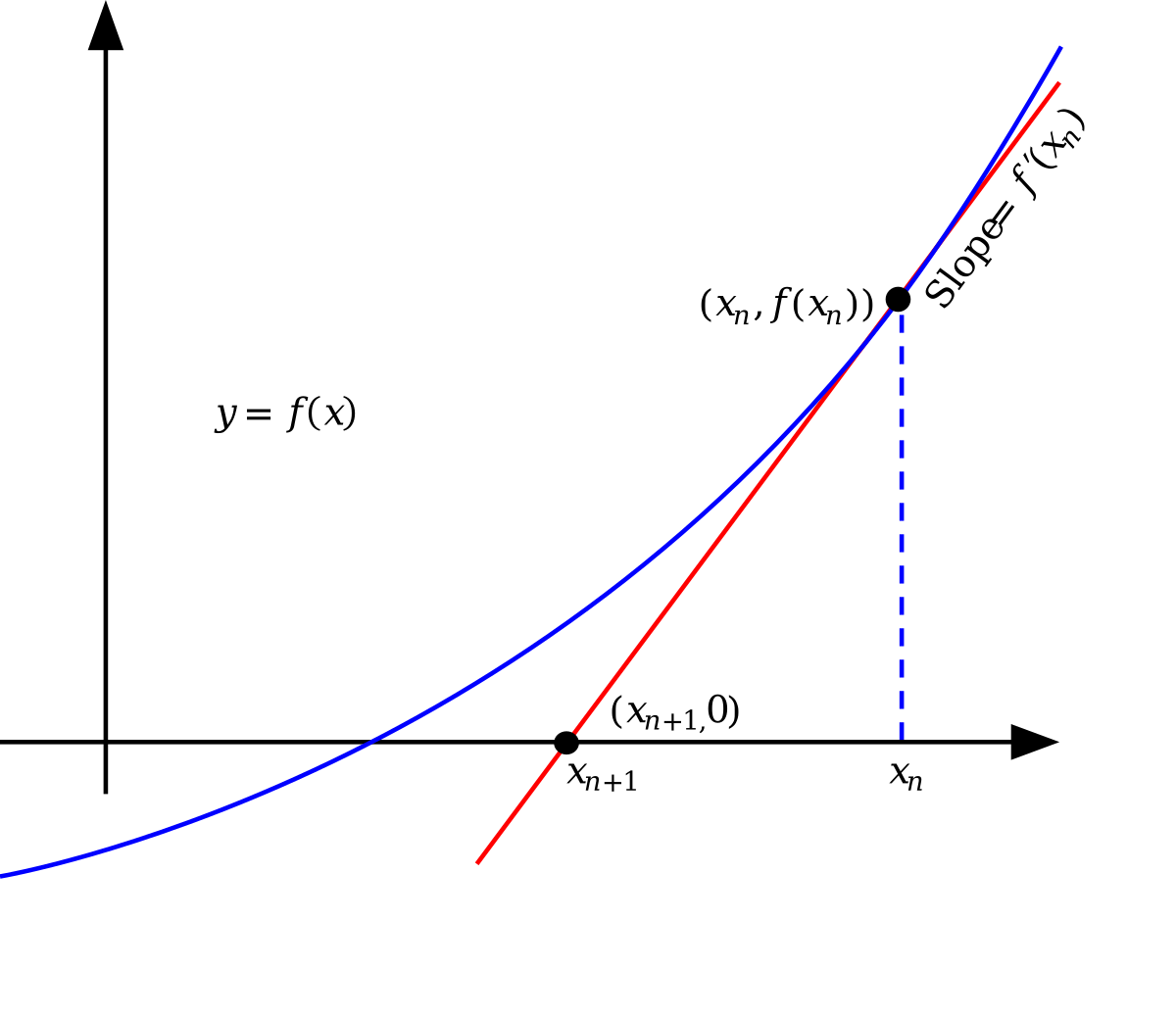
By Original: Olegalexandrov Vector: Pbroks13 - Own work based on: Newton iteration.png, Public Domain, Link

위와 같은 그림의 함수의 해를 찾는다고 가정. 이때 우선 대충 x₀으로 찍어봄. 처음부터 잘 찍는 방법도 있는데, 일단 이건 나중에 얘기하도록 하고, 우선 일단 찍었다고 가정. 이때 이 점 ( x₀, f(x₀) )에서의 기울기는 그 도함수로 구할 수 있음: f’(x₀). 이때 법선은 다음과 같이 구할 수 있음:

y - f(x₀) = f’(x₀)(x - x₀)

참고로 이때 이 법선이 x축과 접하는 점과 실제 해 사이의 거리가 x₀와 해 사이의 거리보다 작음. 즉, x₀보다 이 법선이 x축과 접하는 점이 실제 해에 더 가까움. 위의 법선의 방정식에서 x축과 접할 때의 x 값을 구해보면:

x_{i + 1} = x_i - f(x_i) / f’(x_i)

으로 구할 수 있음. 여기서 x가 x_{i + 1}, x₀가 x_i임. 이걸 여러번 반복하면 x₀, x₁, … 을 구할 수 있는데, 이 값들은 올바른 조건 내에서는 f의 해에 접근하게 됨.

뉴턴 방법은 상당히 빨리 수렴하기에 몇 번만 반복하면 그만임. 그 속도가 2차 함수의 속도임.

이제 이 방법을 사용해 V - f(θ) = 0, 즉 해를 구하면 됨. 근데 이게 사실 바로 V - f(θ) = 0를 푸는 건 힘들고, V - f(θ)를 최소화하는 방법을 사용함. 이때 이 식을 F(θ)으로 표기하도록 할 것.

여기에 테일러 급수를 활용하여 F(θ)를 근사할 것:

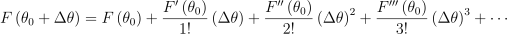
NewtonRaphsonTaylorSeries

이때 (θ₀ + Δθ)이 F(θ)를 최소화하는 값이 되도록 하는 Δθ를 찾을 것임. F’(θ) = 0일 때의 x의 근사값을 얻으려면, 2차 테일러 다항식으로 급수를 줄여서 사용하여 도함수가 0이 되는 지점을 찾으면 됨:

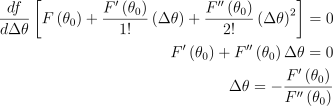
NewtonRaphsonTaylorSeriesSecondOrder

IK에서 이 방법을 사용하려면 뉴턴 방법을 다변수 버전으로 확장해야함. 즉, F’(θ_n)라는 도함수는 ∇F(θ_n)로 표기하며, 이차도함수의 역수였던 1/F’‘(θ_n)는 헤시안 행렬의 역으로 표현해야함: HF(θ_n)^-1.

여기서 헤시안 행렬 H란, 이차편미분으로 이루어진 행렬이다. 즉, H(f(x)) = J(∇f(x))라는 의미.

즉, 각도를 갱신할 때 한 관절에 대해서만 표현할 땐

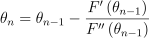
NewtonRaphsonSingleValueUpdate

이렇게만 했을 것임.

하지만 이제는 다변수 함수이므로:

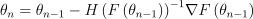
NewtonRaphsonMultivariateUpdate

가 됨.

참고로 이게 더 수렴은 빠르긴 한데, 계산하기엔 이게 더 비싸기도 하고, 헤시안 행렬을 저장해야한다는 점도 있음. 그래서 이거 말고 유사 뉴턴 방법이 선호되는 편임.

5. IK에서의 유사 뉴턴 방법

뉴턴 방법 대신해서 0(해)이나 지역 최대값 등을 찾는 방법임. 야코비나 헤시안을 구할 수 없거나, 매번 구하기 어려울 때 (너무 비싸다거나…) 사용하는 방법.

일단 크게 보면 뉴턴 방법이랑 비슷한데, 몇 가지 다른 점이 있음:

장점: 유사 뉴턴 방법이 계산은 더 빠름
단점: 헤시안 계산에서 정밀도가 떨어져서 수렴이 느림

뉴턴 방법	유사 뉴턴 방법
계산이 비쌈	계산이 쌈
매번 2차 도함수 구해야 함	2차 도함수가 필요 없음
매번 연립일차방정식 풀어야함	연립일차방정식 풀 필요가 없음
수렴이 빠름	수렴이 느림
수렴 경로가 정밀함	수렴 경로가 덜 정밀함

정부호 행렬 definite matrix

x^T가 x의 전치행렬, x^*가 x의 켤레전치행렬, 그리고 0이 n 차원 0벡터라고 할 때,

어떤 n × n 대칭 실수 행렬 M이 Rⁿ에 속한 모든 0이 아닌 x에 대해 x^TMx > 0일 때 M은 양의 정부호 행렬이라 부름. 즉, 모든 고유값이 양수인 경우임.
어떤 n × n 대칭 실수 행렬 M이 Rⁿ에 속한 모든 x에 대해 x^TMx ≥ 0일 때 M은 양의 준정부호 행렬이라 부름. 즉, 모든 고유값이 음수가 아닌 경우임.
어떤 n × n 대칭 실수 행렬 M이 Rⁿ에 속한 모든 0이 아닌 x에 대해 x^TMx < 0일 때 M은 음의 정부호 행렬이라 부름. 즉, 모든 고유값이 음수인 경우임.
어떤 n × n 대칭 실수 행렬 M이 Rⁿ에 속한 모든 x에 대해 x^TMx ≤ 0일 때 M은 음의 준정부호 행렬이라 부름. 즉, 모든 고유값이 양수가 아닌 경우임.

여기서 양의 정부호/준정부호 실수 행렬이 convex 최적화 문제의 기본임. 만약 어떤 점 p에서 어떤 행렬의 헤시안 행렬이 양의 정부호 행렬이라면, 함수는 p 근처에서 convex의 형태를 띠고 있음.

할선법

By Jleedev - Own work in Inkscape 0.42, Public Domain, Link

뉴턴 방법처럼 어떤 함수 f가 주어졌을 때, 할선의 해를 통해 f의 해를 추정하는 방법임. 할선이란 어떤 곡선이 있을 때, 이 곡선과 최소 두 점과 교차하는 선을 의미함.

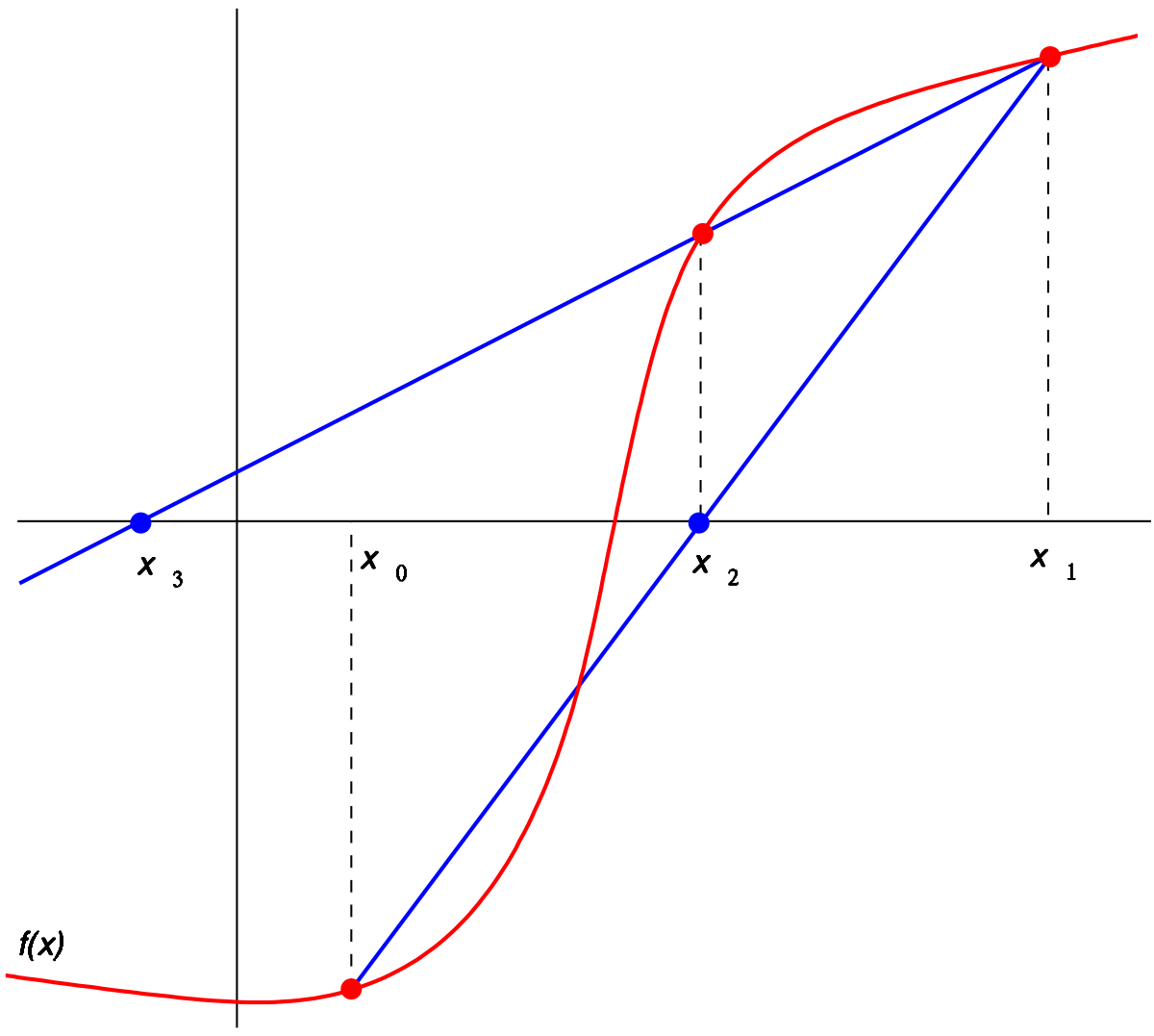
By No machine-readable author provided. Jitse Niesen assumed (based on copyright claims). - No machine-readable source provided. Own work assumed (based on copyright claims)., Public Domain, Link

할선법은 재귀적임:

$SecantMethod$

극값 찾기 (최적화 문제)

어떤 스칼라값을 치역으로 갖는 함수에 대하여 극값을 갖는 문제는 결국 그 함수의 기울기가 0이 되는 지점을 찾는 것임. 다시 말해, f의 기울기가 g라고 할 때, 벡터 함수 g의 0벡터를 찾는 것이 스칼라 함수 f의 극값을 찾는 것임.

g의 야코비 행렬은 f의 헤시안일 것임.

뉴턴 방법의 경우 함수를 지역적으로 근사하는 방법임. 해를 구할 함수를 해 즈음에 극값을 갖는 2차 함수로 표현하고, 1차, 2차 도함수를 통해 그 지점을 찾는 것임.

뉴턴의 방법은 최소화할 함수의 기울기와 헤시안 행렬을 활용함. 유사 뉴턴 방법은 반대로 헤시안 행렬을 구할 필요가 없음. 헤시안은 그냥 연속된 기울기 벡터를 해석하여 갱신함.

뉴턴 방법에선 매번 헤시안을 구하고, 역행렬을 구해야했음.

근데 유사 뉴턴 방법에서는 헤시안을 실제로 구하는게 아니라, 양의 정부호 행렬 B로 근사해서 구하는 것임. 이때 이 행렬은 직전에 구했던 정보를 바탕으로 구할 수 있음. 이때 B를 구하는 방법은 어떤 유사 뉴턴 방법을 쓰느냐에 달려있음. 이때 반드시 지켜야하는 조건이 하나 있음. 바로 헤시안을 근사한 B는 유사 뉴턴 조건(혹은 할선 방정식)을 만족해야함:

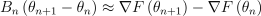
QuasiNewtonCondition0

위의 식을 행렬식으로 다시 작성하면:

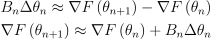
QuasiNewtonCondition1

이제 기울기가 0인 지점을 구해야하니, 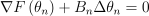GradientIsZero 를 만족해야함. 즉,

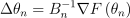
DeltaTheta

할선 방정식 뿐만 아니라, 대부분의 경우 B는 대칭이며, 헤시안이랑 최대한 비슷해야함.

B를 ∇²F(θ_n)로 근사할 때, B가 최대한 계산하기 쉬워야하고, 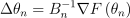DeltaTheta 는 풀기 쉬워야 함.

유사 뉴턴 방법

일반적인 유사 뉴턴 방법의 순서:

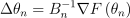풀기
한 턴의 크기(혹은 학습율) t_n 정하기
θ_{n + 1} = θ_n + t_nΔθ_n 업데이트하기 (t가 학습율)
B_n으로 B_{n + 1} 구하기 (사용하는 유사 뉴턴 방법마다 이 단계가 다름)

유사 뉴턴 방법의 기본 아이디어는 이미 헤시안에 대한 정보를 갖고 있는 B_{n - 1}로부터 B_n을 잘 구하는 방법을 사용하는 것임.

유명한 방정식들:

방법	B_{k + 1} =	H_{k + 1} = B_{k + 1}^-1
BFGS	$B_BFGS$	$H_BFGS$
Broyden	$B_Broyden$	$H_Broyden$
Broyden family	$B_BroydenFamily$
DFP	$B_DFP$	$H_DFP$
SR1	$B_SR1$	$H_SR1$

Broyden-Fletcher-Goldfarb-Shanno (BFGS) 방법

BFGS에서는 B 행렬을 다음과 같이 업데이트함:

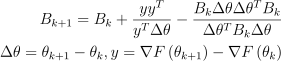
BFGSUpdate

역행렬은 다음과 같이 업데이트 가능:

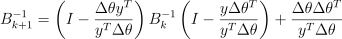
BFGSInverseUpdate

둘 다 O(n²) 정도의 비용이 들음.

만약 y^TΔθ > 0이라면, BFGS는 B_k의 양의 정부호성을 유지함. 다시 말하자면 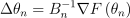DeltaTheta 가 내려가는 방향이라는 것임. 이건 역 행렬 업데이트 공식으로 구할 수 있음:

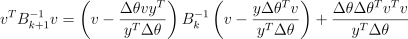
BFGSInverseUpdateRewritten

만약 B_k > 0이고 y^TΔθ > 0라면 두 항은 모든 v에 대해 음수가 아님. 즉, 정부호 행렬의 조건에 따라 B는 양의 정부호 행렬이 됨.

BFGS 업데이트는 할선 조건을 만족함:

Δθ = θ_{k + 1} -θ_k, y = ∇F(θ_{k + 1}) - ∇F(θ_k)일때 B_{k + 1}Δθ = y임.

할선법은 뉴턴 방법을 상당히 손쉽게 변형한 방법으로, 2차 도함수를 모르더라도, 유한차분법을 사용하여 f’로 f’‘를 근사할 수 있음:

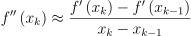
FiniteDifferencing

이걸 다르게 재작성하면:

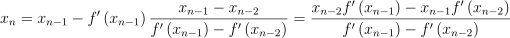
FiniteDifferencingSecantMethod

6. 휴리스틱 IK 알고리듬

Cyclic Coordinate Descent

수치적인 방법으로 관절의 속도를 구하지 말고, 좀 더 유연하면서 절차적인 방법을 사용할 수 있음. CCD는 각 관절을 하나 하나, 밖에서 안 순으로 처리함. 각 관절마다 end effector를 목표로 움직이게 하는 최선의 각도를 구해주는 것임.

CCDFigure

위의 그림에서처럼 총 21 프레임 동안 처리할 때, 0, 5, 10, 15, 20 번째 프레임의 모습임.

CCD의 핵심 알고리듬:

루프 카운터를 0으로
가장 마지막 관절에서 시작
목표를 바라보도록 회전
그 다음 관절로 간 다음 2번으로
첫번째 관절에 도달한 경우, 목표에 도달을 했거나 루프를 사전에 정한 한계만큼 돌렸다면 알고리듬을 종료. 아니라면 루프 카운터 증가시키고 다시 2번으로

여기서 3번에서 목표를 바라보도록 회전한다는 것은 다음 사진으로 이해할 수 있음:

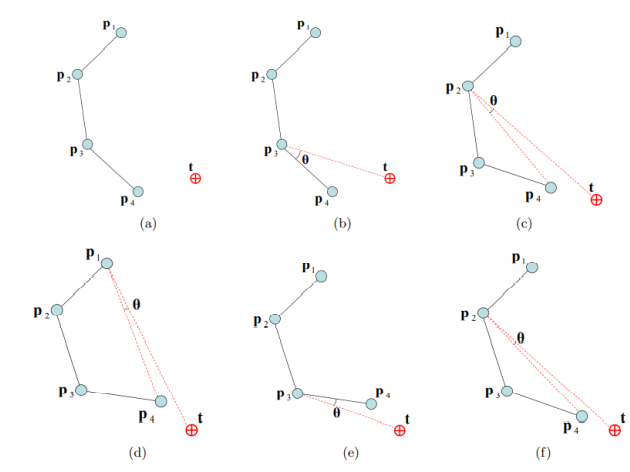
CCDAngleFigure

Triangulation IK

Triangulation IK 방법은 코사인 법칙을 사용해서 관절의 root부터 end effector까지 순차적으로 각도를 계산하는 방법임. 관절에 제약이 없고, 목표가 범위 내에만 있다면 해법을 반드시 구할 수 있음. 또한 CCD과 달리 여러번 연산하는 것이 아닌, 한 번만 훑고 바로 답이 나오기에 계산 비용이 적음.

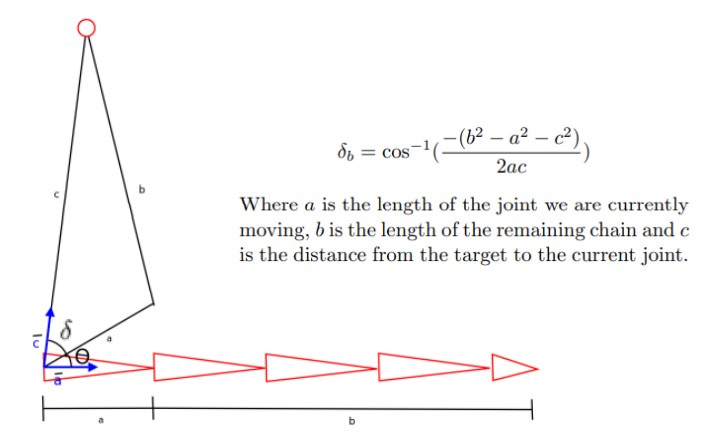
TriangulationIKFigure

하지만 이 방법의 경우 end effector에 가까워질 수록 각도의 변화가 적어 거의 일직선을 유지함. 이 알고리듬 자체가 root에서 시작하기 때문에 root에 가까운 관절들이 제일 많이 바뀔 수 밖에 없음. 게다가 end effector가 한 개 밖에 없는 경우에만 쓸 수 있음. 또한 관절에 제약이 있거나, 목표가 범위 밖에 있으면 사용할 수 없음. 이건 각 관절이 서로 독립적으로 처리되기 때문임.

순차적 IK

순차적 IK(SIK)란 해석-반복적 IK 방법으로 실시간으로 인간을 재구성하는 방법임.

입력값: end effector(손목, 발목, 머리, 골반 등 인간의 포즈를 나타낼 수 있는 뼈들) 위치

알고리듬:

root 관절은 이미 알려진 end effector의 위치로부터 추정함
위에서 추정한 orientation과 root과 head markers의 위치를 합친 혼합 IK 방법으로 척추 설정함
쇄골의 orientation은 쇄골의 end effector의 위치와 척추의 위치로 결정
최종적으로 사지를 end effector 위치에 따라 설정

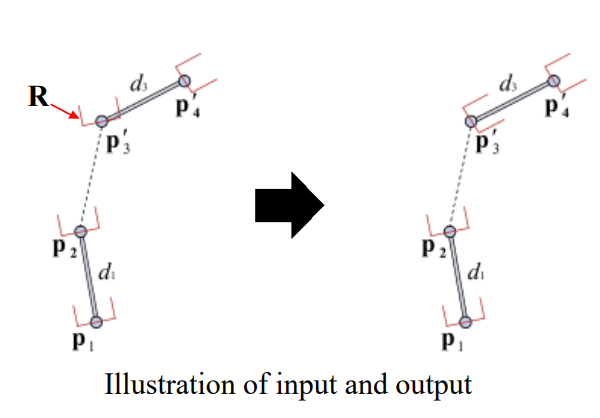
FABRIK

Forward And Backward Reaching IK. 즉 직전에 계산한 관절의 위치를 바탕으로 다음 업데이트 땐 전후방으로 반복하며 관절의 위치를 구함.

기본적으로 업데이트할 때 한 번에 한 관절의 각도를 수정하여 전체 system의 오류를 최소하하는 방법임.

우선 마지막 관절에서 시작해서 앞으로 진행하고, 진행하는 동안 관절들을 수정해주는 것임. 그렇게 첫번째 관절에 도달하면 같은 방법으로 방향만 반대로 진행함. 이러면 한 사이클이 끝난 것임.

다른 방법은 관절의 각도를 정하는데에 반해, FABRIK은 선 위의 점을 찾는 방식으로 각 관절의 위치를 구하기 수렴하는데 필요한 사이클이 적고, 계산 비용도 적고, 시각적으로도 현실적인 결과가 나옴.

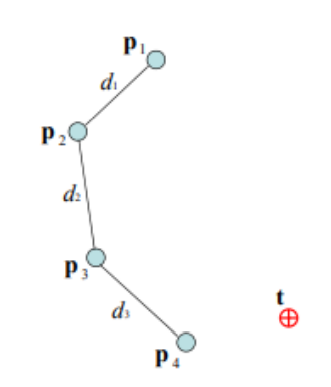
각 관절의 위치를 p_i로 표기하고, p₁이, root, p_n을 end effector로 둠.
목표는 t라 부름.

알고리듬:

각 관절 사이의 길이 d_i를 구함: d_i = |p_{i + 1} - p_i|
목표가 범위 내에 있는지를 판단함. root에서 목표까지의 거리와 모든 d의 합을 비교해주면 됨
만약 범위 내에 있다면 한 사이클을 돌림. 이때 한 사이클은 두 단계로 나뉨
첫번째 단계:
1. end effector부터 root 순으로 각 관절의 위치를 추정함
2. end effector의 새 위치를 목표 위치로 둠, p’_n = t.
3. p_n과 p’_n를 지나는 선 l_{n - 1}을 구함.
4. (n - 1)번째 관절의 새 위치는 p’_n으로부터 선 l_{n - 1}을 따라 d_{n - 1}만큼 떨어진 곳 p’_{n - 1}임.
5. 이걸 다음 관절에 대해서 계속해서 반복함.
6. root, 즉 p’₁까지 다 새롭게 위치를 정했을 때까지 반복함.
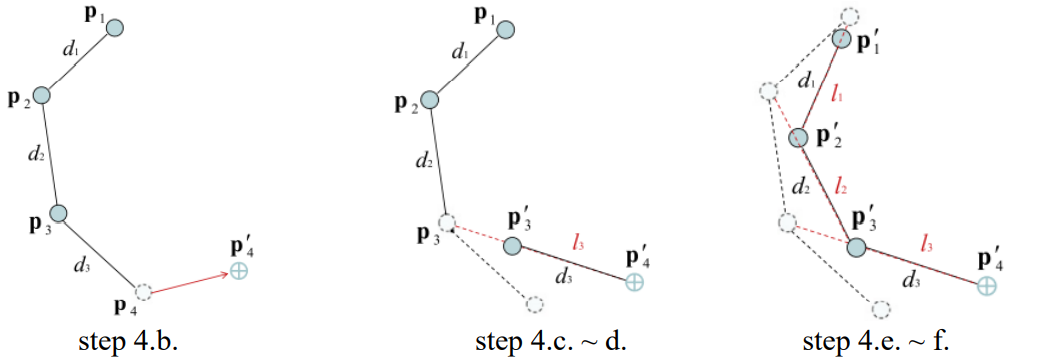
두번째 단계:
1. 방법은 같지만, 이번엔 root에서 end effector 방향으로 진행
2. 첫번째 관절, 즉 root의 새 위치 p’‘₁는 root의 초기 위치 p₁으로 둠.
3. 점 p’‘₁과 p’₂을 잇는 선 l₁을 활용하여 p’‘₁에서 선 l₁을 따라 d₁만큼 떨어진 곳에 있는 p’‘₂을 두번째 관절의 새 위치로 선정.
4. end effector까지 이 방법을 적용함
한 사이클이 끝나면 end effector이 거의 목표 근처에 근접해있을 것임.
end effector가 목표와 같아지거나 적당히 근접할 때까지 이 방법을 반복함.

FABRIKFigure0

FABRIKFigure1

FABRIKFigure2

end effector가 여러 개 인 경우

end effector가 여러 개가 있는 경우 손쉽게 확장할 수 있음. 이를 위해선 root 뿐만 아니라 subbase 관절, chain의 개수와 구조 등이 필요함.

subbase 관절이란 두 개 이상의 chain을 연결하는 관절임. 대표적으로 머리, 척추, 쇄골을 잇는 subbase 관절 등이 있음.

첫번째 단계:
1. 기존과 같지만, 이번엔 각 end effector에서부터 부모 subbase로 이동함
2. 이러면 같은 subbase에 연결된 서로 다른 end effector에 따라 같은 subbase가 서로 다른 위치를 갖게 될 것임.
  - 즉, subbase sb가 두 end effector s1, s2가 있을 때, s1를 따라 FABRIK을 적용하면 sb의 위치가 p1일 것이고, s2를 따라 적용하면 p2일 것임. 이때 이 p1과 p2가 서로 다른 위치라는 것.
3. 이때 이러한 서로 다른 위치들의 중심점을 subbase의 새 위치로 정함
4. 다시 이 subbase부터 그 다음 root(혹은 subbase)로 또다시 FABRIK을 진행함
두번째 단계:
1. 이번엔 root에서 다음 subbase로 진행
2. end effector(혹은 subbase)까지 갈 때까지 각 chain마다 독립적으로 FABRIK을 수행.
3. end effector가 목표에 닿았거나 직전 사이클과 현재 사이클이 그렇게 크게 다르지 않을 경우 종료

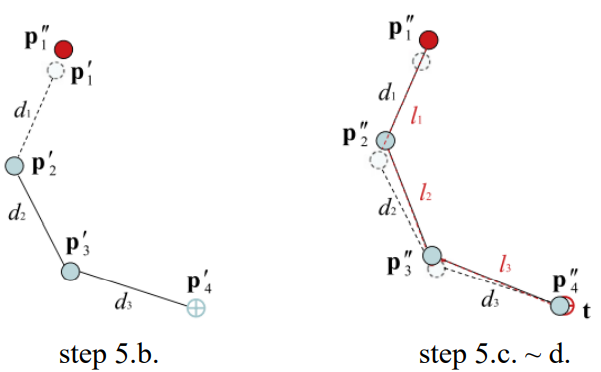
대부분의 인간 모델은 생체역학적 제약이 있는 관절들로 이루어짐. 이 제약들로 인해 인간과 같은 움직임을 보이게 되는 것.

FABRIK은 반복적인 방법이다보니 각 사이클마다 결과로 나온 orientation을 바탕으로 유효한 범위에 있도록 강제하여 관절에 제약을 줄 수 있음. 여기서 핵심 아이디어는 목표를 유효한 범위로 끌고 와서 관절 제약이 언제나 만족하도록 해주는 것임. 다른 관절 제약 방법과는 달리 FABRIK은 3D 문제를 2D 문제로 단순화하기에 그 복잡도나 처리 시간이 줄어 들음.

만약 ball & socket 관절(구상관절)이 있고, 이것이 로터 R과 회전 제약 θ₁, …, θ₄으로 orientational 제약을 준다고 가정. 그러면 이 각도로 관절의 범위를 일종의 콘 유사한 모양으로 만들 수 있게 됨:

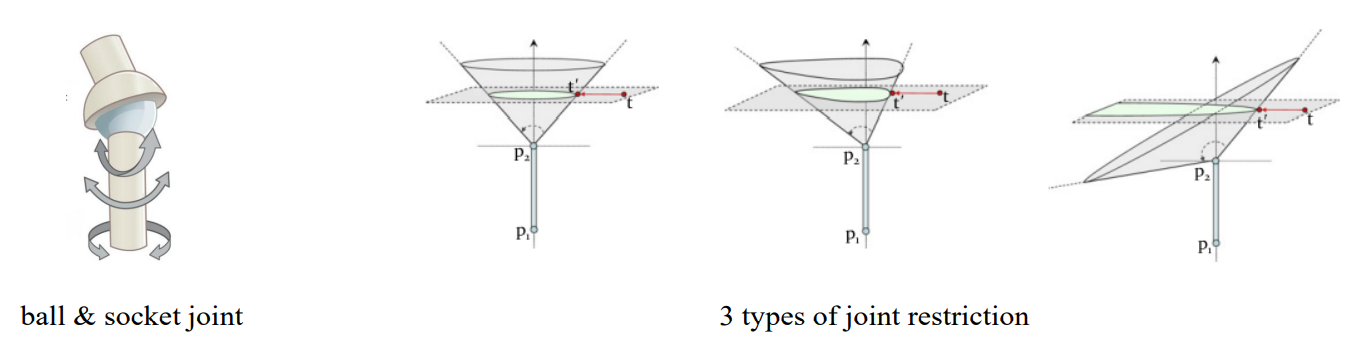
FABRIKJointRestriction

세 가지 범위가 있음:

모든 θ가 같다면, 원형 콘이 생김.
만약 θ가 둘 다 90도보다 작지만 서로 같지 않다면 타원형의 콘이 생김.
만약 θ가 둘 중 하나가 90도보다 크고, 나머지 하나는 90도보다 작다면 포물선형의 콘이 생김.

대부분의 경우엔 2번 케이스임.

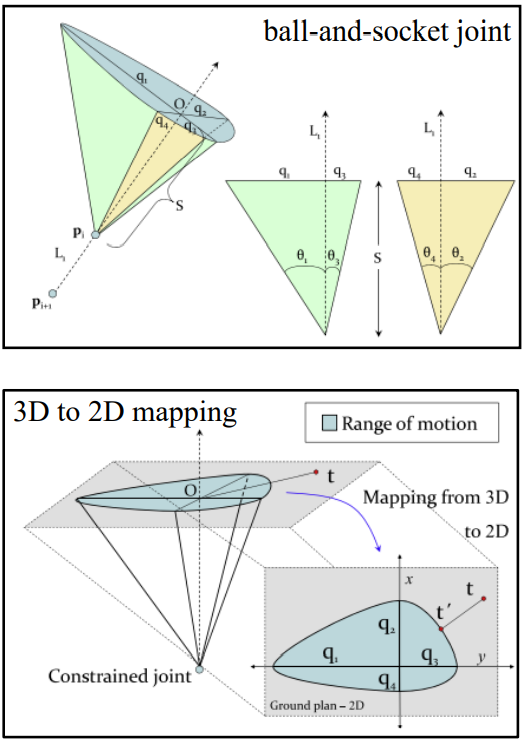
FABRIKEllipsoidalShape

이때 타원은 위의 그림에서처럼 거리 q_j에 의해 정의됨.

관절의 orientation은 다음과 같이 정해짐:

우선 첫번째 단계에 있다고 가정. 즉, p’_i의 새 위치를 구하여 이것으로 (i - 1)번째 관절의 새 위치 p’_{i - 1}를 구하고 있는 중임.
즉, 관절 p’_i와 p_{i - 1}의 orientation을 구할 때 회전을 의미하는 rotor를 찾음. 이때 rotor가 제약보다 더 큰 회전을 한다면, p_{i - 1}이 제약 내에 있도록 규제해줌.

FABRIKEllipsoidalShapeFigure0

7. 게임과 폰트

폰트와 타입페이스

Typeface ⊃ Font

Font	Typeface
특정 스타일과 크기를 갖는 어떤 문자 집합.	같은 디자인을 따르는 문자 / 글자 / 숫자 등의 집합

Typeface
- Helvetica
Font
- Helvetica Regular
- Helvetica Oblique
- Helvetica Bold
- Helvetica Bold Oblique

Typeface

By Max Naylor - Own work, Public Domain, Link

Baseline

인도-유럽어족의 경우 위의 그림에서처럼 어떤 기반 위에 글자를 쓰게 됨. 이때 영어의 ‘p’처럼 baseline 밑으로 뚫고 가는 부분을 descender이라 부름. ‘p’의 body는 baseline 위에 딱 있음.

대부분의 경우:

대문자는 baseline 위에 앉아 있음. J나 Q 정도가 예외사항.
Lining figures(아랍 숫자 등)는 baseline 위에 앉아 있음.
3 4 5 7 9, g j p q y 정도는 descender가 있을 수도 있음.
0 3 6 8 c C G J o O Q 정도는 baseline보다 살짝 아래까지 내려가서(overshoot) baseline 위에 앉아 있다는 착시 현상을 일으키고, 위로는 x-height이나 대문자 크기보다 살짝 위로 올라가서 H x X 1 5 7과 같은 글자와 같은 길이라는 착시 현상을 일으킴.

Body Height, Capital Height, X-Height

Body Height이란 가장 높은 곳부터 가장 낮은 곳 사이의 거리를 의미.

Capital Height이란 플랫한 대문자(M I 등)의 높이를 의미함. S나 A와 같이 둥글거나 뾰족한 애들은 이 높이를 overshoot하여 착시 현상을 줌. 모든 typeface는 고유한 capital height을 가짐.

소문자의 높이가 x-height임. x-height이 큰 typeface가 보통 더 가독성이 좋음.

Ascender, Descender

CC BY-SA 3.0, Link

Public Domain, Link

Ascender과 Descender은 글자의 가독성을 높여줌. 그래서 표지판처럼 가독성이 무조건 좋아야하는 경우 전부 대문자로 쓰지 않는 것임.

가끔 숫자 3 4 5 7 9에도 descender를 사용하는 경우가 있는데, 이런 걸 old-style numeral이라 부름.

Font

By Vectorised by Froztbyte - Own work, Public Domain, Link

Weight이란 보통 폰트의 굵기를 의미함.

일반적으로 다음과 같이 나눔:

Light
Regular
Medium
Bold

Serif

By Recreated by User:Stannered, original by en:User:Chmod007 - en:Image:Serif and sans-serif 01.png, CC BY-SA 3.0, Link

By Recreated by User:Stannered, original by en:User:Chmod007 - en:Image:Serif and sans-serif 03.png, CC BY-SA 3.0, Link

Serif는 끝에 약간 뭔가 뭔가가 있음. 근데 이게 있는게 보통 더 가독성이 좋다고 함. 좀 클래식하고 포멀한 느낌.

Sans-Serif는 끝에 뭐가 없는 것임. sans가 without을 의미하는 프랑스어라고 함. 좀 더 미니멀, 캐주얼한 느낌.

래스터화

By The original uploader was <a href="https://en.wikipedia.org/wiki/User:Aarchiba" class="extiw" title="wikipedia:User:Aarchiba">Aarchiba</a> at <a href="https://en.wikipedia.org/wiki/" class="extiw" title="wikipedia:">English Wikipedia</a>. - Transferred from <a class="external text" href="https://en.wikipedia.org">en.wikipedia</a> to Commons., Public Domain, Link

위처럼 가장 간단한 형태의 래스터화를 bi-level 래스터화라 부름. 그냥 흑백 래스터화 렌더링…

By No machine-readable author provided. <a href="//commons.wikimedia.org/w/index.php?title=User:BenFrantzDale~commonswiki&action=edit&redlink=1" class="new" title="User:BenFrantzDale~commonswiki (page does not exist)">BenFrantzDale~commonswiki</a> assumed (based on copyright claims). - No machine-readable source provided. Own work assumed (based on copyright claims)., CC BY-SA 3.0, Link

가독성을 높이기 위해 일종의 hint를 통해 래스터화가 픽셀 잘 렌더링할 수 있도록 만들어 줌. 의도적으로 폰트의 너비와 높이, 글자 앞뒤의 공백의 크기 등을 수정해주는 것.

위의 그림의 경우 위에가 hinting 없는 경우, 그 아래가 hinting 있는 경우. hinting을 쓴게 좀 더 확실하게 구분이 되는 것을 볼 수 있음.

PostScript 폰트

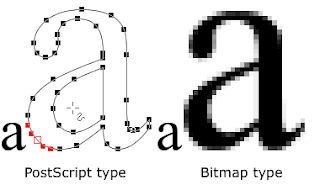
PostScriptText

PostScript 폰트는 폰트의 외곽선에 대한 정보를 주어 베지어 커브로 폰트의 생김새를 결정하는 폰트임.

앤티앨리어싱

폰트를 단순 흑백으로 래스터화하면 사실 좀 자연스럽지 않음. 그래서 앤티앨리어싱 방법을 적용하여 완전 검은색이거나 완전 하얀색인 픽셀이 아니라, 적당히 자연스럽게 gray scale로 폰트를 렌더링하는 방법임.

hinting 없이 안티앨리어싱으로 하면:

By <a href="//commons.wikimedia.org/wiki/File:Rasterization-antialiasing-without-hinting.png" title="File:Rasterization-antialiasing-without-hinting.png">Rasterization-antialiasing-without-hinting.png</a>: The original uploader was <a href="https://en.wikipedia.org/wiki/User:Aarchiba" class="extiw" title="wikipedia:User:Aarchiba">Aarchiba</a> at <a href="https://en.wikipedia.org/wiki/" class="extiw" title="wikipedia:">English Wikipedia</a>. Later version(s) were uploaded by <a href="https://en.wikipedia.org/wiki/User:Riumplus" class="extiw" title="en:User:Riumplus">Riumplus</a> at <a class="external text" href="https://en.wikipedia.org">en.wikipedia</a>. derivative work: <a href="//commons.wikimedia.org/w/index.php?title=User:Orbik&action=edit&redlink=1" class="new" title="User:Orbik (page does not exist)">Orbik</a> (<a href="//commons.wikimedia.org/wiki/User_talk:Orbik" title="User talk:Orbik">talk</a>) - <a href="//commons.wikimedia.org/wiki/File:Rasterization-antialiasing-without-hinting.png" title="File:Rasterization-antialiasing-without-hinting.png">Rasterization-antialiasing-without-hinting.png</a>, Public Domain, Link

hinting 있이 하면:

Public Domain, Link

Subpixel 폰트 렌더링

By <a href="https://de.wikipedia.org/wiki/Benutzer:TMg" class="extiw" title="de:Benutzer:TMg">TMg</a> - Own work. Created in Paint Shop Pro using average resampling. No screenshots used., Public Domain, Link

원래 래스터화는 pixel 별로하는 건데, 폰트는 워낙 작다보니까, 아예 각 pixel의 RGB 영역까지 포함해서 출력을 하자는 것임.

위에서 봤던 sample 글자에 subpixel 기술을 적용하면:

위의 글자를 좀 더 분리해서 보면:

Public Domain, Link

LCD 등에는 어울리지만, CRT에는 어울리지 않는 기술임.

subpixel 기술이 괜찮은 이유는, 상당히 작은 글자의 경우 앤티앨리어싱만 적용하면 오히려 글자가 블러 처리가 되어 잘 안 보일텐데, 이걸 subpixel로 렌더링하면 디테일을 전부 잡아낼 수 있기 때문임.

8. 오디오 프로그래밍

Windows 10 Audio Stack Diagram

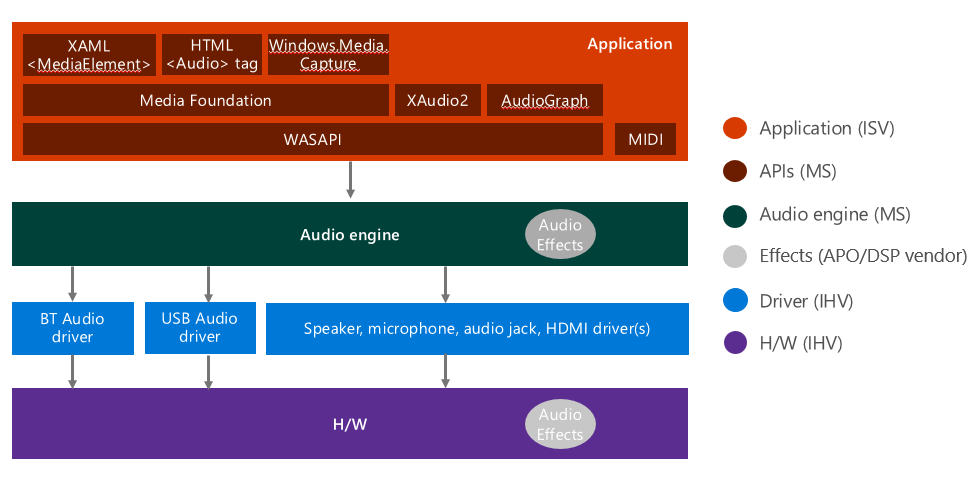
AudioWindows10StackDiagram

API

상위 계층 API: 어플리케이션 개발에 사용함.
- 현재 사용 중인 API:
 - XAML MediaElement 클래스 (C#, VB, C++)
 - HTML Audio 오브젝트, Video 오브젝트 <tags> (웹사이트나 윈도우즈 웹앱에서 사용)
 - Windows.Media.Capture 네임스페이스 (C#, VB, C++)
 - Microsoft Media Foundation (C++)
- 현재 사용 X
 - DirectShow
 - DirectSound
 - PlaySound
 - Windows.Media.MediaControl
하위 계층 API
- 오디오 스트리밍용
  - WASAPI (고성능. 복잡함.)
  - IXAudio2 (게임에서 보통 사용)
  - MIDI
- enumeration용
  - Windows.Devices.Enumeration
- Windows 어플에 추천 X
  - About MMDevice API (Windows.Devices.Enumeration로 대체됨)
  - DeviceTopology API
  - EndpointVolume API

Microsoft Media Foundation

Windows Vista 이후의 Windows에서 디지털 미디어를 다루는 어플리케이션 개발에 사용.

MediaFoundationArchitecture

왼쪽 모델은 미디어 데이터에 대해서 end-to-end 파이프라인을 사용하는 케이스임. 우선 어플리케이션 측에서 파이프라인을 초기화(실행할 파일의 URL을 준다는가)를 한 다음, 스트리밍을 제어할 메서드를 호출함.

오른쪽 모델은 소스로부터 데이터를 빼오거나, 데이터를 destination에 푸시해줌(둘 다도 가능). 이건 데이터 스트림에 직접 접근할 수 있어서 데이터를 처리할 때 유용함.

WASAPI

Windows Audio Session API.

클라이언트 어플리케이션이 어플리케이션과 audio endpoint device 간의 오디오 데이터의 흐름을 관리할 수 있도록 해주는 API.

여기서 Audio Endpoint 장치를 이해하려면 우선 endpoint 장치를 이해하면 됨. endpoint 장치란 데이터 흐름 경로가 시작하거나, 끝나는 하드웨어 장치를 의미함. 흐름이 시작하는 곳이라면 마이크, CD 플레이어, 끝나는 곳이라면 스피커, 헤드폰이 있음.

WASAPI 내부엔 여러 인터페이스가 있는데, 여기에 접근하려면 우선 audio endpoint device에 해당하는 IAudioClinet 인터페이스 오브젝트를 IIMDevice::Activate 메소드로 생성해야함.

MIDI

Musical Instrument Digital Interface (MIDI).

MIDI란 여러 전자 악기나 컴퓨터 등 음악을 연주하거나, 수정하거나, 녹음하는 오디오 장치를 연결하는 어떤 통신 프로토콜, 디지털 인터페이스, 전기 커넥터를 의미하는 기술 표준임.

결국 장치 간 메시지 전달 컨셉에 기반했다는 것이 제일 중요함. MIDI 메시지는 단순히 한 액션에 대한 수치적 정보임. 이 수치적 정보는 누른 key임.

Win32 API는 MIDI 데이터를 처리할 때 다음 인터페이스를 제공함:

Media Control Interface (MCI).
- MCI 시스템이 MIDI 파일을 실행하므로, 어플리케이션에선 MCI를 통해 손쉽게 MIDI 연주 가능.
- 다만, MCI는 MIDI 출력만 지원하며, MIDI 이벤트와 다른 실시간 이벤트 간의 동기화 방법을 제공하지 않음.
- 그러므로 정확한 MIDI 합성이 필요하면 스트림 버퍼나 MIDI 서비스를 사용해야함.
스트림 버퍼
- 어플리케이션이 시간 기반의 MIDI 데이터로 이루어진 버퍼를 수정하여 실행이 가능하도록 함.
- 스트림 버퍼는 MCI보다 더 세밀한 제어가 필요한 어플리케이션에서 사용함.
- MIDI 이벤트의 시간 정보는 MIDIEVENT 구조체의 dwDeltaTime 멤버에 있음.
- 시간은 tick 기준이며, 이 tick은 표준 MIDI 파일 1.0 스펙에 정의되어 있음.
MIDI 서비스
- 가장 MIDI 데이터를 세밀하게 제어해야하는 어플리케이션은 이걸 사용함.
- 진짜 MIDI에 미친 개발자, 즉 MIDI 제어, 시퀀싱 툴 등을 개발한다면 이걸 사용하면 됨.

오디오 엔진

오디오 엔진은 두 성분으로 이루어짐:

오디오 장치 그래프 (audiodg.exe)
- 오디오 엔진을 로딩함
오디오 엔진 (audioeng.dll)
- 오디오 스트림을 믹싱하고 처리함.
- 오디오 신호를 처리하는 특정 하드웨어 전용 플러그인인 오디오 처리 개체 (APO)를 로딩해줌.

오디오 드라이버

오디오 드라이버는:

오디오 스택이 여러 오디오 장치(내장 스피커, 마이크 등)로부터 오디오를 출력 / 입력하게 해줌.

하드웨어

오디오 하드웨어란 예를 들면:

오디오 코덱
DSP (선택 사항)
내장 스피커, 마이크 등
외부 장치: USB 오디오 장치, 블루투스 오디오 장치, HDMI 오디오 등

디지털 오디오

디지털의 형태로 소리를 저장한 것이 디지털 오디오. 보통 순차적으로 수치적인 샘플로 인코딩된 오디오 신호를 의미함. 디지털 오디오 시스템에서는 아날로그 전기 신호를 analog to digital converter (ADC)로 디지털 신호로 변환함. 전기학에서 ADC란 아날로그 신호를 디지털 신호로 변환해주는 시스템이며, 이건 입력을 양자화하기에 약간의 오류나 노이즈가 발생함.

디지털 오디오 기술은 녹음 / 수정 / 대량생산 / 음원 배포(노래, 팟캐스트, 음성 효과 등) 등에 사용함. 과거에는 실제 물리적인 데이터를 팔았음. 아날로그 오디오 시스템이란 소리의 물리적인 파형을 마이크와 같은 변환기로 전기 신호로 변환해줌. 허나 아날로그 오디오 신호는 전기 회로나 관련 장치의 내재적인 특성 때문에 노이즈나 왜곡이 들어갈 수도 있음. 디지털 오디오 신호는 데이터를 저장할 때 correction에 사용하는 인코딩 기술에서나 신호를 전달할 때 오류가 발생할 수 있음.

디지털 오디오 압축

당연히 저장이나 오디오 데이터 전달이 좀 더 효율적이게 됨.

손실 압축이든 무손실 압축이든 어쨋든 정보의 반복을 코딩, 양자화, 이산 코사인 변환, 선형 예측 등으로 줄일 수 있음.

손실 압축 알고리듬의 경우 압축률이 상당히 높아 여러 오디오 어플리케이션에서 사용함.

사실상 심리 음향학psychoacoustics을 사용하여 거의 들리지 않는 소리들의 음질을 죽여 이런 소리들을 저장하거나 전달하는 공간을 줄이게 됨.
압축률은 거의 원본의 80~90%임.
ac-3, mp3, aac, mp4, vorbis, wma 등이 있음

무손실 압축의 경우 원본으로 완벽하게 복원할 수 있도록 디코딩 될 수 있게 디지털 데이터로 저장됨.

압축률은 거의 원본의 50~60% 정도로, 보통 다른 일반적인(영상 포함) 무손실 데이터 압축과 비슷함.
무손실 코덱은 curve fitting이나 선형 예측으로 신호를 추정함.
flac, alac, ape, ofr, wv, tta, mpeg-4 als 등

심리 음향학

심리 음향학이란 음향학과 청각 생리학을 합쳐서 소리의 특징과 청각적인 감각 간의 관계를 결정함.

Loudness란 소리의 강도를 느끼는 정도에 대한 주관적인 측정치임. 이걸로 큰 소리와 작은 소리를 구분할 수 있게 됨.

절대적 청각 임계점
- 조용한 환경에서 청각적인 감각이 발생하는 가장 작은 소리의 압력 정도를 의미함.
- 사람마다, 소리 주파수마다 다름.
불편함 정도
- 불편함을 느끼는 가장 작은 소리 압력의 정도를 의미함.
- 사람마다, 소리 주파수마다 다름.
일반 임계점
- 여러 일반적인 청각을 갖는 사람들로부터 기록한 평균 입계점을 의미.