간단한 퐁 셰이딩 수식 (2022.04.21)

Home

퐁 셰이딩

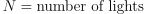
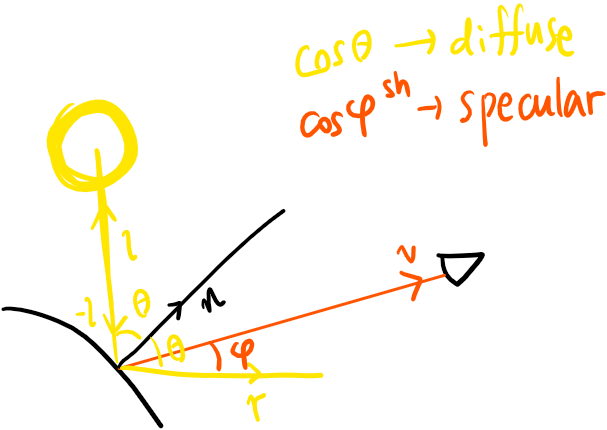
참고: 빛의 방향이라고 해서 광원이 빛을 보내는 방향이라고 생각할 수 있으나, 그래픽스 계에서는 반대로 사용함;; 이건 v도 마찬가지

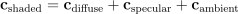
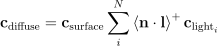
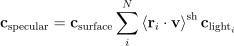
< >⁺은 대충 음수면 0으로 clamp하라는 뜻임. max(lambertian, 0.0f)를 사용하는 방법도 있음.

프로그래머가 직접 정해야하는 값들:

• sh: 얼마나 반짝반짝 맨들 맨들한가?
• a: 각 RGB 별로 ambience를 얼마나 줄 것인가 (보통 0.0 ~ 0.2 등… 직접 실험해보는 것을 추천)

프로그래머가 입력으로 줘야하는 값들:

• N: 빛의 개수. 셰이더 내에 매크로로 대충 정의해두고 어플리케이션과 값 맞춰서 써주면 됨. 대충 일단 퐁 구현할 때는 괜?찮을 듯.
• n: 보통 vertex attribute으로 vertex buffer에 position이랑 같이 있음.
• c_light: constant buffer / uniform 변수로 광원의 색을 알려줘야함. 하얀색 광원만 있는 건 아니니까.

프로그래머가 구해야하는 값들:

• l: 아마 Constant buffer / uniform 변수로 점 광원의 월드 공간에서의 위치를 따로 줬을 텐데, 그 값을 lightPosition이라고 칩시다. 여기에 지금 처리해야할 표면 위의 점의 월드 공간에서의 위치를 정점 셰이더에서 픽셀 / 프래그먼트 셰이더로 넘겨 줬을 것임. 이걸 worldPosition이라 치면, l은 lightPosition - worldPosition임. ㅇㅇ 방향이 반대임 ㅋㅋ
• r: reflect 함수로 구하면 됨. 참고로 여기선 l이 아니라 -l값을 사용해야 제대로 된 반사 방향을 얻을 수 있음 ^_^.
• v: l이랑 마찬가지로 아마 카메라의 월드 공간에서의 좌표를 constant buffer / uniform 변수로 받았을 텐데, 이걸 cameraPosition 변수라 치면, v = cameraPosition - worldPosition임. ㅇㅇ 방향 반대임.
• c_surface: 결국 텍스처에서 샘플링해서 구하면 됨.

디버깅해보기

Normal 값 제대로 들어가나?

VS에서 계산한 월드 공간에서의 normal vector의 값을 그대로 색으로 출력해보기.

근데 이때 법선은 정규 벡터라 값의 범위가 [-1.0f, 1.0f], 즉 음수 값이 나올 수도 있으니, 이걸 RGB로 표현 가능한 [0.0f, 1.0f]의 범위로 축소해줘야함.

즉, 1.0f 만큼 더하고 2.0f 만큼 빼주면 됨:

return float4((normal + 1.0f) / 2.0f, 1.0f);

이런 식.

1. X+ 축의 방향을 바라보는 면
   

이 경우 normal은 (1, 0, 0, 0) 이므로, RGB는 (1, 0.5, 0.5, 1). 즉 핑크색임.

1. X- 축의 방향을 바라보는 면
   

이 경우 normal은 (-1, 0, 0, 0) 이므로, RGB는 (0, 0.5, 0.5, 1). 즉 청록색임.

1. Y+ 축의 방향을 바라보는 면
   

이 경우 normal은 (0, 1, 0, 0) 이므로, RGB는 (0.5, 1, 0.5, 1). 즉 연한 초록색임.

1. Y- 축의 방향을 바라보는 면
   

이 경우 normal은 (0, -1, 0, 0) 이므로, RGB는 (0.5, 0, 0.5, 1). 즉 보라색임.

1. Z+ 축의 방향을 바라보는 면
   

이 경우 normal은 (0, 0, 1, 0) 이므로, RGB는 (0.5, 0.5, 1, 1). 즉 연한 파란색임.

1. Z- 축의 방향을 바라보는 면
   

이 경우 normal은 (0, 0, -1, 0) 이므로, RGB는 (0.5, 0.5, 0, 1). 즉 초갈색임.

View Direction?

1. X+ 축의 방향과 가까워질수록 핑크색

2. X- 축의 방향과 가까워질수록 청록색.

3. Y+ 축의 방향과 가까워질수록 연한 초록색.

4. Y- 축의 방향과 가까워질수록 보라색.

5. Z+ 축의 방향과 가까워질수록 연한 파란색.

6. Z- 축의 방향과 가까워질수록 초갈색.

World Position?

1. X+Y+Z+ 쪽 대각선 꼭지점의 월드좌표 (1, 1, 1, 1) → RGB (1, 1, 1, 1). 하얀색.

2. X+Y+Z- 쪽 대각선 꼭지점의 월드좌표 (1, 1, -1, 1) → RGB (1, 1, 0, 1). 노란색.

3. X+Y-Z+ 쪽 대각선 꼭지점의 월드좌표 (1, -1, 1, 1) → RGB (1, 0, 1, 1). 핑크색.

4. X+Y-Z- 쪽 대각선 꼭지점의 월드좌표 (1, -1, -1, 1) → RGB (1, 0, 0, 1). 핑크색.

5. X-Y+Z+ 쪽 대각선 꼭지점의 월드좌표 (-1, 1, 1, 1) → RGB (0, 1, 1, 1). 하늘색.

6. X-Y+Z- 쪽 대각선 꼭지점의 월드좌표 (-1, 1, -1, 1) → RGB (0, 1, 0, 1). 초록색.

7. X-Y-Z+ 쪽 대각선 꼭지점의 월드좌표 (-1, -1, 1, 1) → RGB (0, 0, 1, 1). 초록색.

8. X-Y-Z- 쪽 대각선 꼭지점의 월드좌표 (-1, -1, -1, 1) → RGB (0, 0, 0, 1). 검은색.

Light Direction?

이번엔 돌아가는 빛과 큐브 위의 점들 사이의 light direction을 구해봅니다…

이번에도 normal과 유사하게 방향마다 값들이 나옵니다.

1. X+ 쪽 핑크색.
2. Z+ 쪽 연한 파란색.
3. X- 쪽 청록색.
4. Z- 쪽 초갈색.

---

N = \textrm{number of lights}
\textbf{c}_{\textrm{shaded}} = \textbf{c}_{\textrm{diffuse}} + \textbf{c}_{\textrm{specular}} + \textbf{c}_{\textrm{ambient}}
\textbf{c}_{\textrm{diffuse}} = \textbf{c}_{\textrm{surface}} \sum_{i}^{N}{\left \langle {\textbf{n}}\cdot{\textbf{l}} \right \rangle^+ \textbf{c}_{\textrm{light}_i}}
\textbf{c}_{\textrm{specular}} = \textbf{c}_{\textrm{surface}} \sum_{i}^{N}{\left \langle {\textbf{r}_i}\cdot{\textbf{v}} \right \rangle^{\textrm{sh}} \textbf{c}_{\textrm{light}_i} }
\textbf{c}_{\textrm{ambient}} = \textbf{c}_{\textrm{surface}} \sum_{i}^{N}{\textbf{c}_{\textrm{light}_i} \textbf{a}_i}