ReSTIR GI: 실시간 경로 추적을 위한 경로 재표집 (2022.04.09)
- 저자
- Yaobin Ouyang. NVIDIA
- Shiqiu Liu. NVIDIA
- Markus Kettunen. NVIDIA
- Matt Pharr.
- Jacopo Pantaleoni. NVIDIA
- 출판일자: 2021.06.24. 목요일.
- 출판: Computer Graphics Forum (Proceedings of High Performance Graphics)
- 연구 분야: 컴퓨터 그래픽스
- 논문 파일: 링크
초록
최근에 GPU 많이 발전해서 광선추적법 하드웨어로 가속할 수 있긴 한데, 실시간 어플리케이션에서는 실질적으로 픽셀 당 추적 가능한 광선의 수가 얼마 안 됨. 그렇기에 경로 추적법을 사용할 경우, 현존하는 가장 성능이 좋은 디노이징 알고리듬을 사용하더라도 해결해야할 문제들이 있음. 최근에 개발한 ReSTIR 알고리듬[BWP*20]의 경우 픽셀당 그림자 광선을 얼마 쓰지 않으면서도 수백만개의 광원이 있는 장면을 고품질로 렌더링할 수 있었음. 하지만 간접 조명을 표집할 좋은 알고리듬이 추가적으로 필요함.
그렇기에 간접광에 대한 병렬 중심 GPU 구조에 적합하면서 성능도 좋은 경로 표집화 알고리듬을 이 논문에서 소개하고자 함. 이 논문의 방법 또한 ReSTIR의 스크린 스페이스 시공간 재표집 원칙에 기반해서 다중 바운스 경로 추적법을 통해 얻은 간접광의 경로를 재표집함. 이를 통해 시간과 이미지의 픽셀에 대해 어떤 경로가 제일 빛에 영향을 많이 주는 중요한 경로인지에 대한 정보를 공유할 수 있음. 결과적으로 이 알고리듬을 통해 경로 추적법에 비해 오류가 상당히 감소함: 이 알고리듬을 사용할 경우, 이 논문에서 사용한 실험 장면 기준 각 프레임마다 모든 픽셀의 한 표본마다 9.3에서 166 배 정도의 범위만큼이나 MSE가 개선되었음. 디노이저까지 사용할 경우 최신 GPU 기준 실시간 프레임율을 보이면서 고품질의 경로 추적 기반 전역 조명을 렌더링할 수 있었음.
1. 도입
경로 추적법은 유연하면서도 일반적임 [Kaj86]. 즉, 복잡한 조명, 재질, 기하를 갖는 장면을 실사에 가깝게 렌더링해주면서도 사용하는 알고리듬은 하나로 통일되어있음. 그렇기에 실시간 렌더링에서 경로 추적법을 선호할 수 밖에 없음. 하지만 워낙 비용이 비싸다보니 하드웨어 가속 광선 추적법이 나왔음에도 실시간 프레임율 기준으로 픽셀 당 겨우 광선 열 몇 개가 최대로 추적이 가능하기에 실시간 분야에서는 경로 추적법을 잘 선호하지 않은지 좀 됐음[McC13, NVI18]. 좋은 디노이징 알고리듬(예를 들어 Scheid et al의 SVGF 알고리듬[SKW*17, SPD18]이나 Munkberg와 Hasselgren의 [MH20]와 같은 신경망을 사용한 방법)이 노이즈가 있는 이미지의 품질을 개선할 수는 있겠지만 그럼에도 애초에 광선을 좀 더 효과적으로 표집하여 장면의 조명에 대한 정보를 좀 더 제공할 수 있도록 하는 것은 중요함.
이 논문의 핵심은 디노이징 이전에 경로 추적법을 사용한 다중 바운스 전역 조명(GI)의 품질을 높이는 것임. 간접광 표집의 효율성을 높여 경로 추적 전역 조명이 실시간에 가능하도록 하는 것이 목표임. 이를 달성하기 위해 Bitterli et al.이 직접 조명을 표집할 때 사용한 ReSTIR 알고리듬, 즉 재표집한 중요도 표집(RIS)[TCE]과 저장소 재표집[Vit85, Cha82]을 합친 방법을 사용함BWP*20.
ReSTIR과의 차이점이라면, ReSTIR은 전역광 공간에서 초기 표집을 하는데에 반해, 이 논문에서는 셰이딩하는 점에서 모든 방향을 의미하는 지역 구 내에서의 공간에서 초기 표집을 함. 해당 광선을 추적하면 장면의 표면 위의 점을 얻을 수 있음; 광선의 원점으로 다시 산란되는 빛의 양이 RIS의 가중치가 됨. 이 점을 다시 시공간에서 재표집하게 되면, 장면의 간접 조명을 근사하는 분포로부터 가중치 표본을 생성할 수 있어 오류가 감소하게 됨.
이 논문에서의 테스트 장면을 기준으로 보면 저장소로부터 대규모 재표집을 할 수 있어 일반적인 경로 추적법에 비해 평균 제곱 오류(MSE)가 9.3에서 166배까지나 향상되었음. 편향되지 않은 몬테 카를로 추정 법칙의 분산이 표본수에 선형으로 비례해서 감소하기 때문에 사실상 경로 추적법이 동일한 MSE를 기록하려면 9.3에서 166배 더 많은 경로를 사용해야함.
이 논문에서 사용하는 방법의 한 가지 주목할만한 점은 저장소와 표본을 저장하는 모든 자료구조는 단순 스크린 스페이스 버퍼임. 즉, 장면의 공간과 독립적임. 경로 가이드 알고리듬처럼 복잡한 월드 공간 자료 구조를 유지하는 것과는 다르게 이 논문에서는 고정된 메모리를 사용하며 병렬로 수정하기도 쉬움; 각 픽셀은 자기 저장소만 수정하며, 근처 픽셀에 있는 저장소에 접근 중일 때, 아무 저장소도 수정이 되지 않고 있음을 어렵지 않게 보장할 수 있음. 그러므로 GPU로 구현 시 성능이 매우 좋음. Unreal Engine 4에서 구현한 ReSTIR GI 알고리듬의 경우 NVIDIA 3090 RTX GPU 기준, 프레임 당 추가적으로 8ms에서 18ms 정도를 요구함.
2. 이전 연구
실시간으로 간접 난반사 전역 조명을 구현하는 방법(예를 들어 [MMSM21, HKL16])은 넘치고 넘침. 대부분의 방법이 상당히 편향되어있어 손쉽게 정량화하기 어려운 반면, 이 논문에서 제시한 방법은 평향이 없거나 평향이 매우 낮기 때문에 비슷한 방법들만 언급하고 넘어갈 것임.
Talbot et al. [TCE05]의 재표집한 중요도 표집 기법에 기반하여 Bitterli et al.은 ReSTIR 알고리듬을 공개함. 이 알고리듬은 직접 조명을 위해 광원 표본에 대한 스크린 스페이스와 시간에서의 재표집을 적용함[BWP*20]. 이 방법에서는 픽셀마다 하나 이상의 빛 표본을 저장한 작은 저장소를 통해 저장소 표집을 적용[Vit85, Cha82]하여 BSDF, 광원과 이진 가시성 항을 곱한 결과를 근사하는 분포로부터 표본을 생성함. 이 알고리듬은 편향된 버전도 있고, 편향되지 않은 버전도 있으며, 둘 다 표본 재사용 및 픽셀 간 정보 공유라는 점 덕에 그 전까지 가장 성능이 좋던 빛 표집 알고리듬에 비해 상당히 오류가 감소했음.
간접광은 직접광에 비해 적분 부분이 근본적으로 더 복잡하고 차원도 높기 때문에 더 다룰 문제들이 많음. 일반적인 경로 추적법에서는 보통 경로 위의 각 정점마다 방향을 지역 BSDF에 잘 맞는 분포에 따라 중요도 표집을 함. 이러한 BSDF 표집 알고리듬이 많이 개발되어왔음; Pharr et al.의 [PJH16] 참고. 물론 간접광의 변화량이 느리면 BSDF 표집이 잘 작동하지만, 상당히 세고 확 구분되는 간접 조명에는 그리 잘 작동하지는 않음.
비균일 간접광이 있을 땐 경로 가이딩path guiding 알고리듬을 사용하여 오류를 상당히 줄여줄 수 있음. 경로 가이딩 알고리듬이란 입사 간접광이나 BSDF과 간접광의 곱에 따라 표집을 해주는 알고리듬임. 경로 가이딩 분야의 초기 연구로는 경로 추적 전처리 기반 5D 공간 방향성 트리를 소개한 Lafortune과 Willems의 연구[LW95], Jensen의 광자 맵[Jen96]과 이를 경로 가이딩에 사용한 연구[Jen95], Jensen의 연구를 개선한 Hey와 Purgathofer의 연구[HP02] 등이 있음. 이 연구에서 제시한 방법들은 우선 전처리로 자료 구조를 만든 다음, 렌더링에 사용한다는 점에서 2패스 방법임. 이 자료구조는 렌더링 시에는 읽기 전용이 되기 때문에 GPU와 같이 병렬성이 높은 아키텍처에 적합하지만, 병렬로 생성하는 방법은 시간이 오래 걸릴 뿐더러 최근에 소개되는 방법에 비해서는 오류 감소가 그리 좋지 않음.
최근에 나온 Vorba et al. [VKS*14]과 Herholz et al. [HEV*16] 등의 연구에서는 가우시안 혼합 모델을 사용하여 렌더링 중에 입사 조명을 학습해줌. Müller와 그의 연구원들은 장면을 팔진트리로 분해하는 적응형 공간적 분해 방법과 사진트리에 기반한 적응형 방향적 분해 방법에 기반한 대중적인 방법을 개발함[MGN17, VHH*19]. Diolatzis et al. [DGJ*20]에서는 이 방법을 조명과 BSDF의 곱을 고려하도록 확장해줌. Ruppert et al.은 공간 분해할 때 셀 간 시차의 효과까지를 고려해준 방법[RHL20]을 소개했으며, Deng et al.은 경로 가이딩을 렌더링에 참여하는 매체에 적용해줌[DWWH20]. 이 방법들이 오류를 상당히 줄여주기는 하지만, 이 구조를 GPU에서 수천개의 스레드로 병렬로 생성해주면 상당한 오버헤드가 발생하기에 실시간 어플리케이션에 적합하지는 않음Pan20. Dittebrandt et al.은 최근에 더 비용이 적으면서 확장성이 있는 경로 가이딩 방법을 공개했음[DHD20].
심화학습을 경로 가이딩에 적용해준 연구 또한 Müller et al.[MMR*19], Zheng과 Zwicker[ZZ19], Bako et al. [BMDS19] 등이 있음. 이 방법들은 경로 표집이 더 효과적이기에 오류 감소가 상당하지만 훈련과 추론이라는 부분 때문에 실시간 어플리케이션에는 적합하지 않음.
Dahm과 Keller이 강화학습을 적용[DK16]해준 연구처럼 다른 학습 방법 또한 경로 가이딩에 사용되었음. 이 논문을 확장시켜 온라인 학습이 고차원 변량 조절과 공간적 방향성 해싱을 통한 실시간 방사 휘도 캐싱을 성공적으로 학습했음[Pan20].
이 논문에서는 직접 경로를 가이드해주는 대신 시간(프레임)과 공간(픽셀)에 대해서 경로 표본을 재사용해줌. 전역 조명에서 경로 재사용을 해준 초기 방법들은 가상 포인트 라이트(VPL)에 기반함[Kel97, DKH*14]. 이 방법들은 광원으로부터 나온 빛의 부분 경로를 표집하여 그들의 정점을 가상 광원으로 재사용하여 카메라에서 가시점들을 비춰줌. 이 방법은 이후에 더 정교한 다중 광원 방법을 적용하고[HPB07] 완전 양방향성 경로 추적 변형들을 적용[PRDD15, CBH*15, TH19]하는 식으로 확장되었음.
카메라로부터 시작한 부분 경로를 재사용하는 방법에 기반한 좀 더 일반적인, 중요한 방법으로는 Bekaert et al. [[BSH02]의 방법이 있음. 본 논문에서는 Bekaert et al.의 방법으로부터 여러 아이디어를 차용함. 사실상 같은 정점 재연결 전략을 사용하면서 ReSTIR 저장소 재표집과 병합 알고리듬을 적용하여 복잡한 추가적인 자료구조 없이, 재사용한 부분경로를 선택하고 가중치를 부여함. 결과적으로는 좀 더 유연한 알고리듬을 얻을 수 있음: Bekaert et al.의 알고리듬의 경우 다중 중요도 표집(MIS) 평가를 할 때 재사용한 표본의 수가 M이라면, O(M2)의 복잡도를 가졌으며, 고정 타일 재사용 패턴(모든 픽셀이 비용을 다같이 부담한다면)을 사용해줘도 O(M)까지 밖에 줄일 수 없음. 허나 이 논문의 ReSTIR 기반 알고리듬의 경우 임의의 재사용 패턴에 대해 O(M)의 복잡도를 가지면서도 시간적 / 공간적 재사용도 가능함.
최근에는 Bauszat et al.이 경사 도메인 렌더링 아이디어를 적용하여 경로 재사용의 효율성을 높였으며[BPE17], West et al.[WGGH20]은 연속 MIS를 적용하여 경로 공간 필터링 알고리듬의 편향을 줄일 수 있음을 보였음[KDB14]. West et al의 알고리듬과는 달리, 이 논문에서는 좀 더 일반적인 시공간적 재사용을 적용하기에 완전히 편향되지 않게 해줄 수 있으며, 실시간 렌더링과 GPU 가속화를 명시적으로 타겟으로 삼음.
3. 배경
실시간 렌더링에서 근본적으로 풀어야하는 문제는 결국 어떤 점 x에서 방향 ω0으로 나가는 방사 휘도를 구할 수 있는 렌더링 방정식을 푸는 것임. 완전히 반사적인 표면의 경우 식은 다음과 같음:
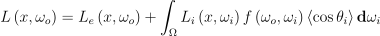
(1)
- L: 나가는 방향의 방사 휘도
- Le: 발산하는 방사 휘도
- Ω: 표면 법선 주위로 방향들이 이루는 반구
- Li: 들어오는 방사 휘도
- f: BSDF
- <cosθi>: 방향 ωi와 표면 법선 간의 각의 코사인 값. 이때 음수는 전부 0으로 클램핑해줌
- dω: 입체각 척도
중간에 참여하는 매체가 없다는 가정하에 입사 방사 휘도 Li는 x에서 ωi 방향으로의 광선에 따라 처음으로 볼 수 있는 표면에서 나가는 방사 휘도에 대하여 다시 써줄 수 있음:
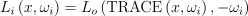
(2)
여기서 TRACE 함수는 x에서 ωi 방향으로 가장 가까운 점을 반환해주는 함수임. 전통적인 몬테 카를로 방법의 경우 다음 추정 법칙을 사용함:
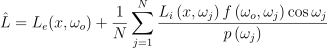
(3)
- N: 고려할 독립적인 표본의 수
- p(ωj): 표본이 이루는 확률 밀도 함수(PDF)
적분 결과가 0이 아닐 때 p(ω) > 0이기만 하면 추정 법칙은 적분에 대해 편향되지 않은 추정치를 제공함(Pharr et al. PJH16 등의 자료를 바탕으로 몬테 카를로 방법과 이를 렌더링에 적용하는 부분에 대한 추가 정보를 참고).
PDF p가 적분과 비슷할수록 몬테 카를로 추정 법칙의 오류가 낮아짐. 재표집 중요도 표집[TCE05]은 직접 표집할 수 없는 복잡한 분포에서 표집을 하는 효과적인 방법임. 표본을 생성할 때 2패스 알고리듬을 사용함. 우선 원본 분포 p(y)로부터 M 개의 후보 표본 y = y1, …, yM을 표집함. 이후 목표 PDF  로부터 아래 확률로 y로부터 표본 z 하나를 재표집함:
로부터 아래 확률로 y로부터 표본 z 하나를 재표집함:
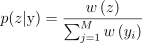
(4)
이때 w(y)는 다음과 같음:
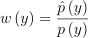
(5)
w(y)는 표본의 상대 가중치임. M이 증가할 수록 z 표본의 분포가  와 더욱 비슷해짐. 재표집을 위해
와 더욱 비슷해짐. 재표집을 위해  을 목표 PDF에 비례하면서 정규화normalize하지 않은 목표 함수로 교체해줘도 됨. 앞으로 이러한 성질을 장점으로 삼을 것이며, 앞으로는
을 목표 PDF에 비례하면서 정규화normalize하지 않은 목표 함수로 교체해줘도 됨. 앞으로 이러한 성질을 장점으로 삼을 것이며, 앞으로는  를 목표 함수로 부를 것임.
를 목표 함수로 부를 것임.
y로부터 재표집한 z가 주어졌을 때, 적분이 0이 아닐 때  > 0이기만 하면 적분
> 0이기만 하면 적분 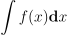 에 대해 편향되지 않은 추정치를 RIS 추정 법칙으로 구할 수 있음:
에 대해 편향되지 않은 추정치를 RIS 추정 법칙으로 구할 수 있음:
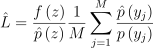
(6)
만약 목표 PDF가 p보다 더 적분과 유사하다면 RIS가 오류를 줄여줌.
Bitterli et al. [BWP*20]에서 보여주었듯, 가중 저장소 표집(WRS)[Vit85, Cha82]을 통해 RIS를 GPU에서 효율적으로 구현할 수 있음. 참고를 위해 WRS 알고리듬을 알고리듬 1에 적어두었으며, 여기에 표본 하나로 저장소를 업데이트하는 함수와 다른 저장소와 병합하는 함수도 포함함. 이 함수를 통해 두 저장소를 고려하여 후보로 뽑은 표본 중 하나를 얻을 수 있음. Bitterli et al.에 따라 이 논문의 저장소 또한 저장소의 한 표본 z의 가중치 W를 저장하며, 이 값은 다음과 같음:
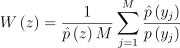
(7)
그러므로 RIS 추정 법칙은 다음과 같이 쉽게 구할 수 있음:
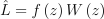
(8)
알고리듬 1: 가중 저장소 표집
1: class Reservoir
2: Sample z
3: w ← 0
4: M ← 0
5: W ← 0 // 7번식
6: procedure Update(Sample S_new, w_new)
7: w ← w + w_new
8: M ← M + 1
9: if random() < w_new / w then
10: z ← S_new
11: procedure Merge(Reservoir r, p^hat)
12: M_0 ← M
13: Update(r.z, p^hat * r.W * r.M)
14: M ← M_0 + r.M
C++-like pseudo code
// GIReservoir.slang
struct GIReservoir
{
// Sample
float3 VisiblePosition; ///< Visible point's position.
float3 VisibleNormal; ///< Visible point's normal.
float3 SamplePosition; ///< Sample point's position.
float3 SampleNormal; ///< Sample point's normal.
float3 SampleRadiance; ///< Sample outgoing radiance.
int M; ///< Input sample count.
float AverageWeight; ///< Average weight for chosen.
uint Age; ///< Number of frames the sample has survived.
}
// GIResampling.cs.slang
bool UpdateReservoir(float weight, GIReservoir srcReservoir, inout TinyUniformSampleGenerator sg, inout float weightSum, inout GIReservoir dstReservoir)
{
weightSum += weight;
dstReservoir.M += srcReservoir.M;
// Conditionally update reservoir
float random = sampleNext1D(sg);
bool bIsUpdate = random * weightSum <= weight;
if (bIsUpdate)
{
dstReservoir.SamplePosition = srcReservoir.SamplePosition;
dstReservoir.SampleNormal = srcReservoir.SampleNormal;
dstReservoir.SampleRadiance = srcReservoir.SampleRadiance;
dstReservoir.Age = srcReservoir.Age;
}
return bIsUpdate;
}
4. ReSTIR GI
원본 ReSTIR 알고리듬[BWP*20]에서는 초기 표본을 소스 PDF p(x)가 빛의 표면에서 균일하게 표집해주는 빛 표집을 통해 구함. 이때 이 빛의 표면은 빛이 발하는 힘에 따라 빛 자체가 표집됨. (원본: The original ReSTIR algorithm places initial samples using light sampling where the source PDF p(x) samples uniformly on the surfaces of lights that are themselves sampled according to their emitted power.) 목표 함수  는 빛 표본에 의해 그림자가 지지 않은 반사된 방사 휘도로 구할 수 있으며, 이때 이 방사 휘도는 발산 방사 휘도, BSDF와 기하학적 결합항의 곱으로 구할 수 있음.
는 빛 표본에 의해 그림자가 지지 않은 반사된 방사 휘도로 구할 수 있으며, 이때 이 방사 휘도는 발산 방사 휘도, BSDF와 기하학적 결합항의 곱으로 구할 수 있음.
ReSTIR로 간접 조명을 표집하기 위해서는 간접 조명에 영향을 주는 방향을 표현해줘야함. 이 표현이 공간의 여러 점에서 시공간적으로 재사용이 가능해야하므로 방향을 의미하는 지역 반구의 단위 벡터는 좋은 표현 방법이 아님. 그러므로 표면 위의 점과 입사 광선을 통해 산란되어 돌아오는 방사 휘도를 연관지음.
여기서 가시점이란 카메라가 각 픽셀에서 장면의 표면 중 가시점을 의미함. 가시점마다 무작위로 방향을 표집한 다음 추적하여 최근접 교차면을 구함. 이때 교차점을 표본점sample point라 부름. 표본 생성은 4.1 섹션에서 좀 더 세부적으로 다루도록 함. 표본점을 생성한 후엔 재표집을 수행한 후 가시점마다 셰이딩 값을 계산해줌(4.2 섹션). 그림 2는 직접광에 대한 ReSTIR과 ReSTIR GI를 비교하며, 그림 4에서는 알고리듬을 요약해줌.
알고리듬은 세 개의 이미지 크기 버퍼를 관리함. 이 버퍼는 각 픽셀에 다음과 같은 값을 저장함:
- 초기 표본 버퍼:
Sample형(그림 3의 초기 표본에 대한 버퍼.) - 시간적 저장소 버퍼: 픽셀에서 직전에 생성된 표본에 WRS를 적용하여 얻은 표본을 저장하는
Reservoir의 버퍼. - 공간적 저장소 버퍼: 근처 픽셀에서의 표본에 WRS를 적용하여 얻은 표본을 저장하는
Reservoir의 버퍼.
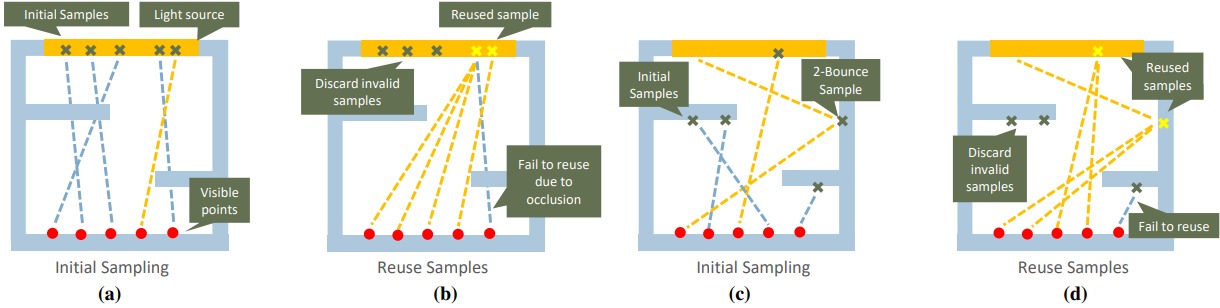
그림 2: ReSTIR과 ReSTIR GI. (a) 원본 ReSTIR 알고리듬[BWP*20]은 장면에서의 빛에서 무작위로 표본을 생성하는 것으로 시작함. (b) 재표집 이후 아무런 영향을 주지 않는 표본을 버림; 유용한 표본은 시공간적으로 공유하며 이들의 기여도에 따른 확률에 따라 사용함. (c) 이 논문에서 제시한 방법의 경우 무작위 방향을 표집하고, 광선을 추적하여 최근접 교차점을 찾아 초기 표본을 생성함. 이때 교차점에서 경로 추적법을 통해 반사 방사 휘도를 계산함. (d) 시공간 재표집을 비슷한 방법으로 적용해줌. 이를 통해 의미 있는 간접 조명을 주는 방향을 찾을 수 있음. 이건 ReSTIR에서는 해주지 못했음.
struct Sample
float3 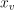 ,
, 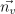 // 가시점과 표면 법선
float3
// 가시점과 표면 법선
float3 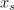 ,
,  // 표본점과 표면 법선
float3
// 표본점과 표면 법선
float3 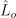 // 표본점으로부터 나가는 RGB 방사 휘도
float3 Random // 경로에 사용할 임의의 수
// 표본점으로부터 나가는 RGB 방사 휘도
float3 Random // 경로에 사용할 임의의 수
그림 3: 표본 표현. Sample은 표본에서의 지역 기하와 나가는 방사 휘도 값과 표본점을 생성할 때 사용한 가시점에서의 지역 기하를 둘 다 저장해줌. 가시점 기하와 경로 추적에 사용할 임의의 수는 섹션 4.3에서 설명할 표본 검증 알고리듬에 사용함.
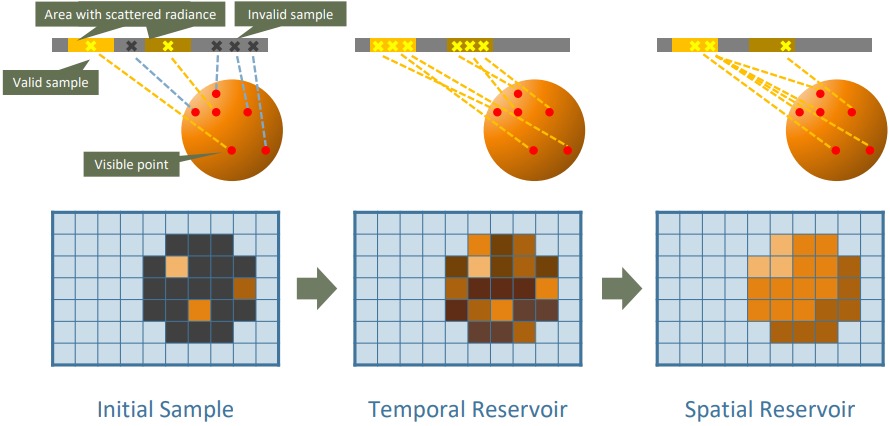
그림 4: 알고리듬 작업 흐름. 각 프레임마다, 각 픽셀마다 다음 단계를 수행해줌: 초기 샘플링: 가시점(빨간 점)마다 임의의 방향으로 광선을 추적하여 최근접 교차점을 스크린 스페이스 초기 표본 버퍼에 저장함. 교차점의 위치, 법선과 방사 휘도, 다음 이벤트 추정 때 사용할 임의의 숫자, 픽셀의 위치와 법선을 저장함. 시간적 재사용: 초기 표본 버퍼에서의 표본과 현재 프레임에서 생성된 표본 중 하나를 임의로 선택하여 시간적 저장소 버퍼를 업데이트해줌. 시간적 재투영을 적용하여 해당 시간적 저장소를 이전 프레임으로부터 찾아냄. 공간적 재사용: 이웃 픽셀 중 임의의 한 시간적 저장소를 선택하여 공간적 저장소를 업데이트해줌. 편향을 억제하기 위해 선택한 픽셀의 깊이와 법선을 현재 픽셀의 깊이와 법선으로 비교해주어 비슷한 기하학적 특징을 갖는 픽셀을 선택함.
4.1. 표본 생성
ReSTIR GI 알고리듬의 첫번째 단계는 각 가시점마다 새 표본점을 생성하는 단계임. 우선 입력으로 G-버퍼를 받는데, 이때 버퍼엔 각 픽셀마다 가시점의 위치와 표면 법선을 갖고 있음. 광선 추적 우선 가시성과 손쉽게 사용할 수 있긴 함.
각 픽셀 q와 이에 대응하는 가시점 xv마다 소스 PDF pq(ωi)를 통해 한 방향 ωi을 표집하고, 광선을 추적하여 표본점 xs을 구함. 소스 PDF는 균일분포여도 되고, 코사인 가중 분포여도 되고, 가시점에서의 BSDF에 기반한 분포여도 됨(6 장에서 이 분포를 비교함). 알고리듬 2의 의사 코드를 참고.
각 표본점마다 나가는 방사 휘도 Lo(xs ωo)를 계산해줌. 이때 ωo는 가시점으로의 방향 정규 벡터임. 이 방사 휘도 값은 여러 가지 방법으로 구할 수 있음. 여기서는 각 정점마다 후사건 추측(NEE)과 다중 중요도 표집을 사용하여 몬테 카를로 경로 추적법을 사용해주었음. 만약 오로지 직접광만이 방사 휘도 추측값에만 있다면 이 알고리듬에서는 단일 튕김 전역 조명만 계산함. 일반적으로는 이후 n 번 경로 추적할 튕김들이 n + 1 튕김 전역 조명에 대응함. 그림 5 참고.
알고리듬 2: 초기 표집
- 각 픽셀 q마다
- G버퍼에서 가시점 xv와 법선
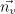 구함
구함 - 소스 PDF pq에서 임의의 방향 ωi로의 광선을 표집
- 광선 추적하여 표본점 xs와 법선
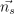 을 구함
을 구함 - xs에서 나가는 방사 휘도
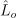 추정.
추정. - InitialSampleBuffer[q] ← Sample(xv,
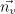 , xs,
, xs, 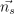 ,
, 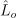 );
);
- G버퍼에서 가시점 xv와 법선
// ScreenSpaceReSTIR.slang
void SetGIInitialSample(uint2 pixel, float3 visiblePosition, float3 visibleNormal, float3 samplePosition, float3 sampleNormal, float3 sampleRadiance, float srcPDF, int reservoirIndexOffset=0)
{
GIReservoir initialSample;
initialSample.VisiblePosition = visiblePosition;
initialSample.VisibleNormal = visibleNormal;
initialSample.SamplePosition = samplePosition;
initialSample.SampleNormal = sampleNormal;
if (dot(initialSample.SampleNormal, initialSample.VisiblePosition - initialSample.SamplePosition) < 0)
{
initialSample.SampleNormal *= -1;
}
if (dot(initialSample.VisibleNormal, initialSample.SamplePosition - initialSample.VisiblePosition) < 0)
{
initialSample.VisibleNormal *= -1;
}
initialSample.SampleRadiance = sampleRadiance;
initialSample.AverageWeight = srcPDF == 0.f ? 0.f : 1.f / srcPDF; // 1;
initialSample.M = 1;
initialSample.Age = 0;
uint sampleIndexOffset = reservoirIndexOffset;
uint pixelIndex = getPixelIndex(pixel);
WriteReservoir(initialSamples, pixelIndex, sampleIndexOffset, frameDim.x * frameDim.y, initialSample);
}
// GIReservoir.slang
void WriteReservoir(RWStructuredBuffer<PackedGIReservoir> reservoirBuffer, uint baseIndex, uint sampleIndex, uint elementCount, GIReservoir reservoir)
{
uint index = baseIndex + sampleIndex * elementCount;
reservoirBuffer[index] = reservoir.pack();
}
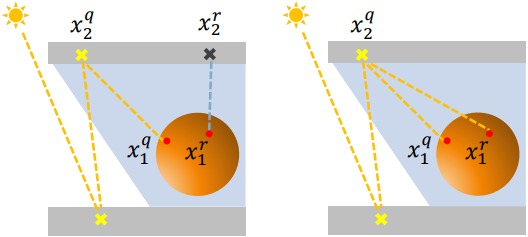
그림 5: 다중 튕김 GI. 각 표본점 x2*마다 대응하는 가시점에 산란된 방사 휘도를 경로 추적법으로 추정함. 최종 경로 정점에 연결하여 다른 가시점이 전체 경로의 기여도를 재사용할 수 있게됨.
4.2. 재표집과 셰이딩
초기 표본을 갓 구한 이후 시공간 재표집을 적용함. 목표 함수
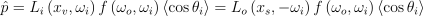
(9)
에는 가시점에서의 BSDF의 효과와 코사인 항까지 포함하고 있음. 물론,
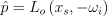
(10)
함수와 같이 단순한 목표 함수도 잘 작동은 함. 픽셀 하나에 대한 목표 함수 중 제일 좋은 것은 아니지만, 사용해보니 초기에 생성된 픽셀을 제외한 픽셀에 대해서 효과적이라는 점에서 공간 재표집을 할 때엔 유용함.
초기 표본을 생성한 후에 시간적 재표집을 적용함. 이 단계에서는 각 픽셀마다 초기 표본 버퍼에서 표본 하나를 읽어온 다음, 이를 통해 식 5와 소스 PDF를 표집한 방향 pq(ωi)에 대한 PDF로서 사용하고,  를 식 10대로 사용하여 RIS 가중치를 구해주어 무작위로 시간적 저장소를 업데이트해줌. 시간적 재표집 의사 코드는 알고리듬 3에 제시하였음.
를 식 10대로 사용하여 RIS 가중치를 구해주어 무작위로 시간적 저장소를 업데이트해줌. 시간적 재표집 의사 코드는 알고리듬 3에 제시하였음.
알고리듬 3: 시간적 재표집
- 각 픽셀 q마다
void execute(const uint2 pixel)
{
...
for (uint localIndex = 0; localIndex < reservoirCount; ++localIndex)
{
// Read latest samples generated by create gather point shader.
uint initialSampleIndex = kReSTIRGIUseReSTIRN ? localIndex : 0;// 1;
// LINE 2
GIReservoir initialSample = ReadReservoir(initialSamples, pixelIndex, initialSampleIndex, frameDim.x * frameDim.y);
int indexOffsetBegin = 2 * localIndex;
int temporalSourceIndex = indexOffsetBegin;
int spatialSourceIndex = indexOffsetBegin + 1;
int temporalTargetIndex = temporalSourceIndex;
int spatialTargetIndex = spatialSourceIndex;
// Use input samples only.
if (kReSTIRMode == ReSTIRMode::InputOnly)
{
WriteReservoir(reservoirs, pixelIndex, temporalTargetIndex, frameDim.x * frameDim.y, initialSample);
WriteReservoir(reservoirs, pixelIndex, spatialTargetIndex, frameDim.x * frameDim.y, initialSample);
continue;
}
// Temporal Reuse.
// Read temporal reservoir.
// LINE 3
GIReservoir temporalReservoir = ReadReservoir(prevReservoirs, prevIdx, temporalSourceIndex, frameDim.x * frameDim.y);
if (length(temporalReservoir.VisiblePosition - worldPosition) > 1.f)
{
isPrevValid = false;
}
float3 radiance = initialSample.SampleRadiance;
temporalReservoir.M = clamp(temporalReservoir.M, 0, temporalMaxSamples);
if (!isPrevValid || temporalReservoir.Age > maxSampleAge)
{
temporalReservoir.M = 0;
}
// Compute reuse weight.
float tf = EvalTargetFunction(temporalReservoir.radiance, worldNormal, worldPosition, temporalReservoir.SamplePosition, evalContext);
float jacobian = 1.f;
if (enableTemporalJacobian)
{
float3 offsetB = temporalReservoir.position - temporalReservoir.creationPoint;
float3 offsetA = temporalReservoir.position - worldPosition;
float RB2 = dot(offsetB, offsetB);
float RA2 = dot(offsetA, offsetA);
offsetB = normalize(offsetB);
offsetA = normalize(offsetA);
float cosA = dot(worldNormal, offsetA);
float cosB = dot(temporalReservoir.creationNormal, offsetB);
float cosPhiA = -dot(offsetA, temporalReservoir.normal);
float cosPhiB = -dot(offsetB, temporalReservoir.normal);
if (cosA <= 0.f || cosPhiA <= 0.f || RA2 <= 0.f || RB2 <= 0.f || cosB <= 0.f || cosPhiB <= 0.f)
{
tf = 0.f;
}
// assuming visible
// Calculate Jacobian determinant and weight.
const float maxJacobian = enableJacobianClamping ? jacobianClampThreshold : largeFloat;
jacobian = RA2 * cosPhiB <= 0.f ? 0.f : clamp(RB2 * cosPhiA / (RA2 * cosPhiB), 0.f, maxJacobian);
tf *= jacobian;
}
float wSum = max(0.f, temporalReservoir.AverageWeight) * temporalReservoir.M * tf;
print("tf", tf);
float pNew = EvalTargetFunction(radiance, worldNormal, worldPosition, initialSample.SamplePosition, evalContext);
// LINE 4
float wi = initialSample.AverageWeight <= 0.f ? 0.f : pNew * initialSample.AverageWeight;
// LINE 5: Update temporal reservoir.
bool selectedNew = updateReservoir(wi, initialSample, sg, wSum, temporalReservoir);
print("wSum", wSum);
float avgWSum = wSum / temporalReservoir.M;
pNew = EvalTargetFunction(temporalReservoir.radiance, temporalReservoir.VisibleNormal, temporalReservoir.VisiblePosition, temporalReservoir.SamplePosition, evalContext);
// LINE 6
temporalReservoir.AverageWeight = pNew <= 0.f ? 0.f : avgWSum / pNew;
print("avgWSum", avgWSum);
print("pNew", pNew);
print("temporalReservoir.AverageWeight", temporalReservoir.AverageWeight);
temporalReservoir.M = clamp(temporalReservoir.M, 0, temporalMaxSamples);
temporalReservoir.Age++;
temporalReservoir.VisiblePosition = worldPosition;
temporalReservoir.VisibleNormal = worldNormal;
// LINE 7
WriteReservoir(reservoirs, pixelIndex, temporalTargetIndex, frameDim.x * frameDim.y, temporalReservoir);
...
}
}
시간적으로 사용해준 다음엔 공간적 재사용을 적용해줌. 근처 픽셀의 시간적 저장소에서 표본을 갖고 와서 또다른 공간적 저장소에 재표집해줌. (알고리듬 4의 의사 코드 참고.) 공간적 재사용을 할 땐 반드시 픽셀 간 소스 PDF의 차이를 고려해야함. 왜냐면 이 알고리듬에서의 표집 스킴은 가시점의 위치와 표면 법선에 기반하기 때문임. (본래 ReSTIR 알고리듬의 경우 각 픽셀의 지역 기하를 고려하지 않고, 바로 직접적으로 빛을 표집했기에 이러한 정정이 필요 없었음.) 그러므로 픽셀 q에서 온 표본을 픽셀 r에서 재사용하고 싶다면 반드시 입체각 PDF를 현재 픽셀의 입체각 공간으로 변환해주어야함. 이 변환은 해당 변환의 야코비 행렬식으로 나누어지는 식으로 해주는 것임[KMA*15, 식 13]:
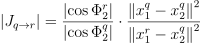
(11)
이때 x1q와 x2q는 각각 재사용 경로의 첫번째와 두번째 정점이며, x1r는 종착 픽셀으로부터의 가시점이고, Φ2q와 Φ2r은 벡터 x1q - x2q와 x1r - x2q가 x2q에서의 법선과 이루는 각임(그림 6). 그림 7을 통해 이 항이 얼마나 중요한지 볼 수 있음.
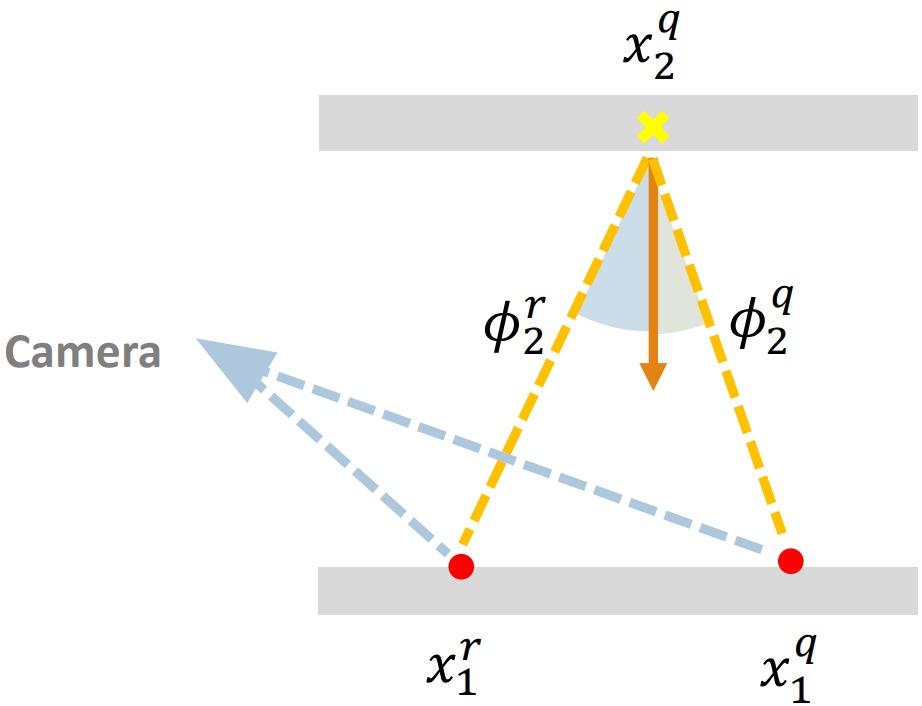
그림 6: 만약 가시점 x1q이 다른 자시점 x1r에서 재사용될 표본점 x2q을 생성했다면, 식 11에서의 야코비 행렬식은 xqq 자체가 표본점 x2q를 다른 확률로 생성했을 것이라는 사실을 고려해줌.

그림 7: 공간적 재표집에서 식 11, 야코비 행렬식의 영향. 벽은 태양빛을 받아 땅바닥에 간접광을 줌. 맨 위: 빛에서 야코비 결과를 무시할 경우 땅바닥의 불연속성을 무시하고 벽과 땅이 붙은 부분에서의 빛을 과도하게 추정함. 중간: 야코비가 추가되어 위와 같은 이상한 점들이 처리됨. 맨 밑: 경로 추적을 한 실제 사진.
공간 재표집 알고리듬 의사 코드는 알고리듬 4에 주어져 있음. 이 알고리듬에는 Bitterli et al.[BWP*20]의 기하 유사도 테스트를 포함하고 있음. 이 유사도 테스트를 통과하려면 표면 법선이 25˚ 내여야 하고, 두 정규 깊이가 0.05 내여야 함.
시공간 재사용이 끝나면 가시점 xv이 간접 조명에 의하여 최종적으로 산란한 방사 휘도를 RIS 추정 법칙인 식 6를 통해 구할 수 있음. 여기서 공간 저장소 W의 가중치가 f(y)를 제외한 모든 항을 제공함. f(y)의 경우 BSDF, 코사인 항, 그리고 저장소 표본의 나가는 방사 휘도의 곱으로 구함.
알고리듬 4: 공간적 재표집
1: for each pixel q do
2: Rs ← SpatialReservoirBuffer[q]
3: Q ← q
4: for s=1 to maxIterations do
5: 임의의 이웃 픽셀 qn 선택
6: q와 qn 기하학적 유사성 계산
7: if 유사성이 주어진 기준보다 낮다면 then
8: continue
9: Rn ← TemporalReservoirBuffer[qn]
10: |Jqn → q| 계산 (식 11)
11: 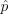 'q ←
'q ← 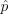 q(Rn.z)/|Jqn → q|
12:
q(Rn.z)/|Jqn → q|
12: 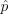 'q ←
'q ← 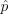 q(Rn.z)/|Jqn → q|
13: if Rn의 표본점이 q의 xv에서 보이지 않는다면 then
14:
q(Rn.z)/|Jqn → q|
13: if Rn의 표본점이 q의 xv에서 보이지 않는다면 then
14: 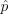 'q ← 0
15: Rs.Merge(Rn,
'q ← 0
15: Rs.Merge(Rn, 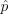 'q)
16: Q ← Q ∩ qn
17: Z ← 0
18: for each qn in Q do
19: if
'q)
16: Q ← Q ∩ qn
17: Z ← 0
18: for each qn in Q do
19: if 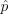 qn > 0 then
20: Z ← Z + Rn.M (편향 정정)
21: Rs.W ← Rs.w / (Z ·
qn > 0 then
20: Z ← Z + Rn.M (편향 정정)
21: Rs.W ← Rs.w / (Z · 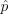 q(Rs.z)) (식 7)
22: SpatialReservoirBuffer[q] ← Rs
q(Rs.z)) (식 7)
22: SpatialReservoirBuffer[q] ← Rs
void execute(const uint2 pixel)
{
...
for (uint localIndex = 0; localIndex < reservoirCount; ++localIndex)
{
...
// Spatial Reuse.
// Read spatial reservoir.
// LINE 2
GIReservoir spatialReservoir = readReservoir(prevReservoirs, prevIdx, spatialSourceIndex, frameDim.x * frameDim.y);
spatialReservoir.M = max(0, spatialReservoir.M);
if (!isPrevValid || spatialReservoir.Age > maxSampleAge)
{
spatialReservoir.M = 0;
}
// Add near sample to s reservoir.
uint prevIdx2;
GIReservoir neighborReservoir = temporalReservoir;
float wSumS = max(0.f, spatialReservoir.AverageWeight) * spatialReservoir.M * EvalTargetFunction(spatialReservoir.SampleRadiance, spatialReservoir.VisibleNormal, spatialReservoir.VisiblePosition, spatialReservoir.SamplePosition, evalContext);
// Determine maximum iteration based on current sample count.
// If sample count is low, use more iterations to boost sample count.
const float fastReuseRatio = 0.5f;
const float fastReuseThreshold = spatialMaxSamples * fastReuseRatio;
const int normalIteration = 3;
const int fastReuseIteration = 10;
int maxIteration = spatialReservoir.M > fastReuseThreshold ? normalIteration : fastReuseIteration;
const float searchRadiusRatio = 0.1f;
float searchRadius = frameDim.x * searchRadiusRatio;
// Initialize reuse history.
float3 positionList[10];
float3 normalList[10];
int MList[10];
int nReuse = 0;
int reuseID = 0;
positionList[nReuse] = worldPosition;
normalList[nReuse] = worldNormal;
MList[nReuse] = spatialReservoir.M;
nReuse++;
spatialReservoir.VisiblePosition = worldPosition;
spatialReservoir.VisibleNormal = worldNormal;
// Search and reuse neighbor samples.
const uint startIndex = sampleNext1D(sg) * kNeighborOffsetCount;
// LINE 4
for (int i = 0; i < maxIteration; i++)
{
// Get search radius.
const float radiusShrinkRatio = 0.5f;
const float minSearchRadius = 10.f;
searchRadius = max(searchRadius* radiusShrinkRatio, minSearchRadius);
// LINE 5: Randomly sample a neighbor.
float3 randOffset = sampleNext3D(sg);
randOffset = randOffset * 2.f - 1.f;
int2 neighborID = prevID + randOffset.xy * searchRadius;
uint2 boundary = frameDim.xy - 1;
neighborID.x = neighborID.x < 0 ? -neighborID.x : (neighborID.x > boundary.x ? 2 * boundary.x - neighborID.x : neighborID.x);
neighborID.y = neighborID.y < 0 ? -neighborID.y : (neighborID.y > boundary.y ? 2 * boundary.y - neighborID.y : neighborID.y);
// LINE 6: Check geometric similarity.
float4 neighborNormalDepth = unpackNormalDepth(prevNormalDepth[neighborID]);
// LINE 7
if (!evalContext.isValidNeighbor(neighborNormalDepth, normalThreshold, depthThreshold))
continue;
// Read neighbor's spatial reservoir.
prevIdx2 = toLinearIndex(neighborID);
bool bReuseSpatialSample = (kReSTIRMode == ReSTIRMode::TemporalAndUnbiasedSpatial ? i % 2 == 1 : 0);
// LINE 9
neighborReservoir = ReadReservoir(prevReservoirs, prevIdx2, bReuseSpatialSample ? spatialSourceIndex : temporalSourceIndex, frameDim.x * frameDim.y);
// Discard black samples.
if (neighborReservoir.M <= 0)
{
continue;
}
// Calculate target function.
float3 offsetB = neighborReservoir.position - neighborReservoir.creationPoint;
float3 offsetA = neighborReservoir.position - worldPosition;
float pNewTN = evalTargetFunction(neighborReservoir.radiance, worldNormal, worldPosition, neighborReservoir.position, evalContext);
// Discard back-face.
if (dot(worldNormal, offsetA) <= 0.f)
{
pNewTN = 0.f;
}
float RB2 = dot(offsetB, offsetB);
float RA2 = dot(offsetA, offsetA);
offsetB = normalize(offsetB);
offsetA = normalize(offsetA);
float cosA = dot(worldNormal, offsetA);
float cosB = dot(neighborReservoir.creationNormal, offsetB);
float cosPhiA = -dot(offsetA, neighborReservoir.normal);
float cosPhiB = -dot(offsetB, neighborReservoir.normal);
if (cosB <= 0.f || cosPhiB <= 0.f)
{
continue;
}
if (cosA <= 0.f || cosPhiA <= 0.f || RA2 <= 0.f || RB2 <= 0.f)
{
pNewTN = 0.f;
}
bool isVisible = evalSegmentVisibility(computeRayOrigin(worldPosition, worldNormal), neighborReservoir.position);
if (!isVisible)
{
pNewTN = 0.f;
}
// Calculate Jacobian determinant and weight.
const float maxJacobian = enableJacobianClamping ? jacobianClampThreshold : largeFloat;
float jacobian = RA2 * cosPhiB <= 0.f ? 0.f : clamp(RB2 * cosPhiA / (RA2 * cosPhiB), 0.f, maxJacobian);
float wiTN = clamp(neighborReservoir.avgWeight * pNewTN * neighborReservoir.M * jacobian, 0.f, largeFloat);
// Conditionally update spatial reservoir.
bool isUpdated = updateReservoir(wiTN, neighborReservoir, sg, wSumS, spatialReservoir);
if (isUpdated) reuseID = nReuse;
// Update reuse history.
positionList[nReuse] = neighborReservoir.creationPoint;
normalList[nReuse] = neighborReservoir.creationNormal;
MList[nReuse] = neighborReservoir.M;
nReuse++;
// Expand search radius.
const float radiusExpandRatio = 3.f;
searchRadius *= radiusExpandRatio;
}
// Calculate weight of spatial reuse.
float m;
if (kReSTIRMode == ReSTIRMode::TemporalAndBiasedSpatial)
{
m = spatialReservoir.M <= 0.f ? 0.f : 1.f / float(spatialReservoir.M);
}
else if (kReSTIRMode == ReSTIRMode::TemporalAndUnbiasedSpatial)
{
// Trace extra rays if unbiased spatial reuse is enabled.
float totalWeight = 0.f;
float chosenWeight = 0.f;
int nValid = 0;
int Z = 0;
for (int i = 0; i < nReuse; i++)
{
bool isVisible = true;
bool shouldTest = true;
float3 directionVec = spatialReservoir.position - positionList[i];
if (dot(directionVec, normalList[i]) < 0.f)
{
shouldTest = false;
isVisible = false;
}
if (shouldTest)
{
isVisible = evalSegmentVisibility(computeRayOrigin(positionList[i], normalList[i]), spatialReservoir.position);
}
// Discard new sample if it is occluded.
if (isVisible)
{
if (kReSTIRMISWeight == 0)
totalWeight += MList[i];
else
{
float misWeight = saturate(dot(normalList[i], normalize(directionVec))) * luminance(spatialReservoir.radiance);
totalWeight += misWeight * MList[i];
if (reuseID == i)
{
chosenWeight = misWeight;
}
}
nValid++;
}
else if (i == 0)
{
break;
}
}
if (kReSTIRMISWeight == 0) m = totalWeight <= 0.f ? 0.f : 1.f / totalWeight;
else m = totalWeight <= 0.f ? 0.f : chosenWeight / totalWeight;
}
pNew = EvalTargetFunction(spatialReservoir.radiance, worldNormal, worldPosition, spatialReservoir.SamplePosition, evalContext);
float mWeight = pNew <= 0.f ? 0.f : 1.f / pNew * m;
spatialReservoir.M = clamp(spatialReservoir.M, 0, spatialMaxSamples);
float W = wSumS * mWeight;
// TODO: add UI control for this
const float maxSpatialWeight = enableSpatialWeightClamping ? spatialWeightClampThreshold : largeFloat;
spatialReservoir.AverageWeight = clamp(W, 0.f, maxSpatialWeight);
spatialReservoir.Age++;
// LINE 21: Write spatial reservoir.
WriteReservoir(reservoirs, pixelIndex, spatialTargetIndex, frameDim.x* frameDim.y, spatialReservoir);
}
}
4.3. 편향
본래 ReSTIR 알고리듬처럼 ReSTIR GI 알고리듬도 편향된 버전과 편향되지 않은 버전 두 가지가 있음. 몇몇 편향의 원인은 쉽게 정정할 수 있지만, 몇 개는 좀 몇 가지 일을 해야할 수도 있음(광선 추적 등). 어느 수준의 성능을 요구하느냐에 따라, 즉 더 나은 성능을 위해 편향을 희생하여 여러 편향을 필요로할 수도 있음. 편향은 시공간 재사용 둘 다에서 발생할 수 있으며, 둘 다 다룰 것임.
직접광에서의 ReSTIR과 마찬가지로 공간적 재표집은 여러 소스 PDF가 서로 다른 픽셀에서 사용되기 때문에 편향이 발생할 수 있음. 만약 다른 픽셀의 저장소에서의 표본을 재사용했을 때, 해당 픽셀의 소스 PDF가 현재 픽셀의 영역을 커버하지 않는다면 추정치에 편향이 발생함. 이 편향은 가시성 광선을 추적하여 어떤 소스 분포가 최종적으로 선택한 표본을 표집할 수 있는지를 확인하고, 이에 따라 결과에 가중치를 부여하는 식으로 정정해줄 수 있음[WP21]. (이 테스트는 알고리듬 4의 18번 줄에 해당함.) 다른 방법으로는 픽셀 간 기하 유사도 테스트를 추가해주는 식으로 광선 추적 없이도 편향을 줄일 수 있음.
그림 9에서 편향 표본 재사용과 무편향 표본 재사용의 차이를 보여줌. 이 그림의 경우 목표 함수를 나가는 빛의 방사 휘도와 난반사와 정반사 성분을 포함한 BSDF 항으로 이루어져있음. 특히 그림자 영역에서 가시성의 변화 때문에 편향이 주로 나옴. 목표 함수가 광택 반사를 포함하고, 정반사 방향으로 표본을 더 주기 때문에 운 나쁘게도 복잡한 가시성 변화가 발생함. 그렇기에 의자 다리 근처에서의 광택진 바닥 쪽의 편향이 더욱 심함.

그림 9: 공간적 재사용에 의한 편향. 좌측: 무편향 결과. 중간: 편향된 결과. 우측: 10× 차이. 특히 그림자 영역에서 가시성의 변화 때문에 편향이 주로 나옴. 목표 함수가 광택 반사를 포함하고, 정반사 방향으로 표본을 더 주기 때문에, 의자 다리 근처에서의 광택진 바닥 쪽의 편향이 더욱 심함.
공간적 재사용에 의한 편향을 줄이는 다른 방법은 공간적 저장소가 알고리듬 4에서처럼 근처 픽셀의 공간적 저장소에서 작동하는 것이 아닌, 근처 픽셀의 시간적 저장소에서만 작동하도록 해주는 것임. 이러면 편향된 표본을 여러번 재표집하여 편향이 누적되는 현상을 막을 수 있음. 하지만 공간적 저장소만 사용할 경우 새롭게 시야에 등장한(즉, 가려지지 않은) 픽셀이 충분한 표본을 수집할 수 없게 될 수도 있어 가시적인 노이즈가 발생할 수 있음. 이 경우 입력 표본의 수가 적은 공간 저장소의 경우 근처 공간 저장소를 재사용하여 수렴 속도를 향상시킴. 그림 10에서 전체 데이터 흐름을 볼 수 있음.
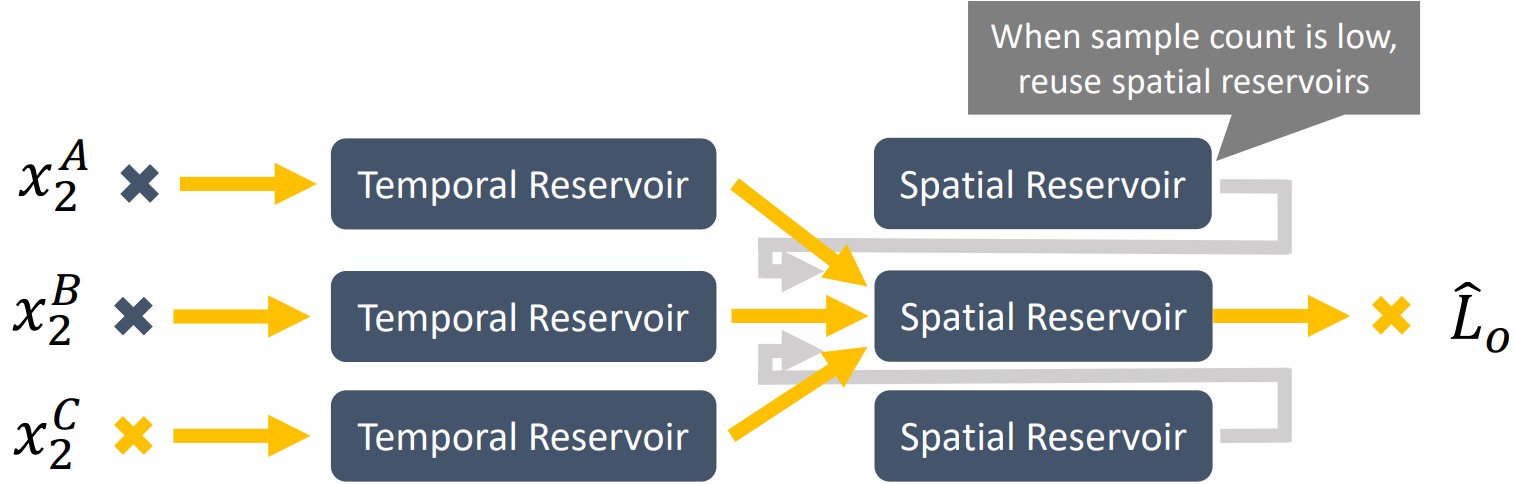
그림 10: ReSTIR GI의 데이터 흐름도. 매 프레임마다 각 픽셀의 시간적 저장소가 새롭게 생성된 표본을 받아들임. 언제나 다른 공간적 저장소를 재사용하는 대신 각 공간 저장소는 오로지 근처 픽셀의 시간 저장소를 재사용하여 편향을 억제함. 표본 수가 적으면 공간 저장소는 다른 공간 저장소를 재사용하여 수렴을 부스팅해줌.
4.2 섹션에서 언급했듯, ReSTIR GI는 BSDF 표집에 의해, 소스 분포가 각 픽셀의 지역 기하에 의존하기에 편향이 발생할 수도 있음. 특정 영역 단위에 대한 같은 분포는 서로 다른 픽셀의 입체 공간에서 서로 다른 모양을 가짐. 이러한 차이점을 고려하지 않고 표본을 재사용하면 편향이 발생함. 이 편향은 식 11을 통해 손쉽게 정정할 수 있음. 이 식은 계산 비용이 낮기 때문에 사용해주지 않을 이유가 없음.
조명이나 장면의 기하가 프레임마다 바뀔 때, 시간적 재사용을 해줄 때 표본점에서 나가는 방사 휘도 값이 정확하지 않으면 편향이 발생함. 게다가 ReSTIR 특성상 저장소 내에 다른 걸로 교체되기 전까지는 상대적으로 밝은 표본을 계속해서 갖고 있으려고 하기에 이 문제가 더욱 심화될 수 있음. 결과적으로 간접 조명을 업데이트하는데 상당한 렉이 걸릴 수도 있음. 이 문제를 완화하기 위해 A-SVGF 디노이징 필터에서 영감을 얻은 표본 검증 메커니즘을 적용함[SPD18]. 매 몇번째 프레임마다 광선을 재추적하여 모든 저장소 표본의 나가는 방사 휘도를 다시 계산해주고, 결과적으로 나오는 방사 휘도가 주어진 수용 범위를 만족하는지를 확인하고, 만족하지 않는다면 저장소를 비워줌. (이 단계에서는 표본을 초기에 생성할 때와 같은 임의의 수가 무작위 표집에 사용되는지 여부가 중요함.) 표본 검증을 위한 프레임 간격은 장면이 얼마나 변하느냐에 따라 조정해줄 수 있음.
동적인 장면에서 시간적 편향의 또다른 원인으로는 표본점을 처음 생성한 이후 가시점과 표본점 사이에 광선을 막는 엄폐물에 의해 발생함. 이 편향은 표본 검증 때 가시점에서 표본점으로 그림자 광선을 추적함으로써 정정 가능.
5. 구현
6. 결과
6.1. 한계
7. 결론 및 향후 연구
감사의 글
참고문헌
L\left (x, \omega_{o} \right ) = L_{e} \left (x, \omega_{o} \right ) + \int_{\Omega} {L_i \left ( x, \omega_{i} \right )f\left(\omega_{o}, \omega_{i} \right )\left \langle \cos{\theta_{i}} \right \rangle \textbf{d}\omega_{i}}
\hat{L} = L_{e}(x, \omega_{o}) + \frac{1}{N}\sum_{j = 1}^{N}{\frac{L_{i}\left(x, \omega_{j} \right )f\left(\omega_{o}, \omega_{j} \right )\cos{\omega_{j}}}{p\left(\omega_{j} \right )}}
p(z | \textrm{y}) = \frac{w\left(z \right )}{\sum_{j=1}^{M}{w\left(y_{i} \right )}}
w\left(y \right ) = \frac{\hat{p}\left(y \right )}{p\left(y \right )}
\hat{L} = \frac{f\left(z \right )}{\hat{p}\left(z \right )} \frac{1}{M} \sum_{j = 1}^{M}{\frac{\hat{p}\left(y_{j} \right )}{p\left(y_{j} \right )}}
W\left(z \right ) = \frac{1}{\hat{p}\left(z \right )M}\sum_{j = 1}^{M}{\frac{\hat{p}\left(y_{j} \right )}{p\left(y_{j} \right )}}
\hat{p} = L_{i}\left(x_{v}, \omega_{i} \right )f\left (\omega_{o}, \omega_{i} \right )\left \langle \cos{\theta_{i}} \right \rangle = L_{o}\left(x_{s}, -\omega_{i} \right )f\left (\omega_{o}, \omega_{i} \right )\left \langle \cos{\theta_{i}} \right \rangle
\hat{p} = L_{o}\left(x_{s}, -\omega_{i} \right )
\left |J_{q\rightarrow r} \right |=\frac{\left | \cos{\Phi_2^r} \right |}{\left | \cos{\Phi_2^q} \right |}\cdot\frac{\left \| x_1^q - x_2^q \right \|^2}{\left \| x_1^r - x_2^q \right \|^2}