지형에 일관된 식물상과 동물상 저작하기 (논문 번역) (2022.03.31)

Home

저자:

• 피에르 에꼬르미에-노까. Pierre Ecormier-Nocca, LIX, Ecole Polytechnique/CNRS, Institut Polytechnique de Paris, France. pierre.ecormier@polytechnique.edu
• 기욤 꼬르도니에. Guillaume Cordonnier, ETH Zürich, Switzerland and Inria, Université Côte d’Azur, France. guillaume.cordonnier@inria.fr
• 필립 까레. Philippe Carrez, Immersion Tools, France. guillaume.cordonnier@inria.fr
• 안-마리 모아뉴. Anne-Marie Moigne, Muséum national d’Histoire naturelle - UMR 7194, HnHp, MNHN, UPVD, CNRS, France. anne-marie.moigne@cerptautavel.com
• 푸랑 메마리. Pooran Memari, LIX, CNRS/Ecole Polytechnique, Institut Polytechnique de Paris, France. , memari@lix.polytechnique.fr
• 베드리히 베네쉬. Bedřich Beneš, Purdue University, USA. bbenes@purdue.edu
• 마리-폴 까니. Marie-Paule Cani, LIX, Ecole Polytechnique/CNRS, Institut Polytechnique de Paris, France. marie-paule.cani@polytechnique.edu

초록

지형에 식물상과 동물상을 서로의 상호작용까지 고려하여 저작하는 새로운 방법을 소개하는 논문. 이 논문에서 소개하는 알고리듬을 통해 각 종별 밀도 맵, 일상 루틴으로 이루어진 안정된 상태의 생태계를 만들어줄 수 있으며, 지형의 침식, 기후적 조건, 생물학적 정보를 갖는 종들로부터 수정된 지형을 만들어줄 수 있음. 자원 접근 그래프Resource Access Graph라는 새로운 자료 구조로 먹이 사슬과 지형의 자원을 얻기 위해 움직이는 동물들 간의 상호작용을 인코딩 해줌. 이 논문에서 제공하는 새로운 경쟁 알고리듬은 이 자료를 바탕으로 초식동물과 육식동물을 모두 아우르는, 지속적으로 안정된 상태의 먹이사슬 솔루션을 제공함. 이 모든 결과는 즉각적으로 적용할 수 있어 실시간으로 맵을 수정해줄 수도 있음. 이를 통해 야생 생물의 영향(초식동물들이 풀을 먹는 등)과 지형 침식을 적용할 수 있음. 또한 이 방법을 현존하는 생태계와 고생물학 전문가들을 통한 이용자 검증으로 정량적으로 검증하여 우리의 시스템이 충분히 다양한 기후에 따른 다양한 생태계를 동일한 지형에서 보일 수 있었음.

1. 도입

지형이 이쁘려면 기후, 침식, 식생, 동물과 같은 여러 요소들 간의 상호작용이 있어야 함. 얘네가 분명 지형에 영향을 주는데, 얘네를 전부 합쳐서 고려해주는 게 쉬운 건 아님. 지금까지 대부분의 경우는 기후, 침식, 식물 생태계나 고려했지 동물상은 맨 마지막에 따로 직접 추가해줬음.

우선 이 논문에서 제시하는 첫번째 관찰은 “동물이 시야에 보이지 않더라도 지형에 시각적인 영향을 준다”는 것임. 동물 간 공간과 자원의 경쟁을 통해 식생을 없애고 길이 생기는 등의 상황이 발생함. 그래서 지금까지 동물을 무시하고 지형에 식물을 깔고 나서 동물을 추가하던 파이프라인을 수정해야 함.

두번째 관찰은 여러 생물체가 공존하는 지형을 만드는게 시뮬레이션 없어도 일관성을 유지하면서 만들어줄 수 있고, 사용자가 손쉽게 제어할 수 있게 만들어줄 수도 있음. 가상 환경을 디자인하시는 분들의 목적은 자신의 의도한대로 관객을 충분히 환경에 몰입하게 해주는 것임. 당연히 이 논문의 결과가 실제 환경과 비슷하면 생물학자들이나 고생물학자들에게도 이득임. 시간 축을 통해 시뮬레이션이 진행되는 시스템의 경우 사용자가 직접 개입을 적극적으로 하기 힘드니까 우리 시스템이 더 나은?듯.

우리 방법이 퀄리티 좋은 CG 지형을 만들어내는 이유는 일관적이면서도 식물상과 동물상 둘 다 포함하는, 제어가 가능한 생태계를 만들기 때문임. 식물도 고려하고, 동물도 고려하고, 심지어 먹이 사슬도 다 고려해줌. 이걸 하위 계층부터 상위로 반복적으로 처리해줌. 사용자 입장에서 직관적으로 수정도 가능하고, 일관적으로 배치된 식물들과 일상 생활에 따라 행동하는 동물들이 존재하는 결과도 바로 볼 수 있음.

이 논문의 시스템을 사용할 경우 보통 입력 지형에 대해서 기후를 정의해주고, 심을 식물들의 종, 초식동물 종, 육식동물 종을 입력해주고, 추가적으로 경쟁 이후 얼만큼의 비율로 있을지에 대한 정보도 주게 됨. 이 입력에 대한 출력은 결국 생태계가 나올 것임. 이 생태계는 주어진 지형에 종이 존재하는 밀도 맵으로 표현이 됨. 당연히 수정 가능. 각 먹이사슬 단계마다, 생성된 개체 하나 하나 마다의 영향이 해당 개체가 소비할 자원으로 역전파됨. 개체와 자원 둘 간의 경로를 연산하여 해당 경로에서의 방목, 먹이 탐색 활동, 침식 등을 처리해줌. 이를 전부 적용한 최종적인 지형은 이제 식물상, 동물상과 일관되어있음. 그림 1 참조.

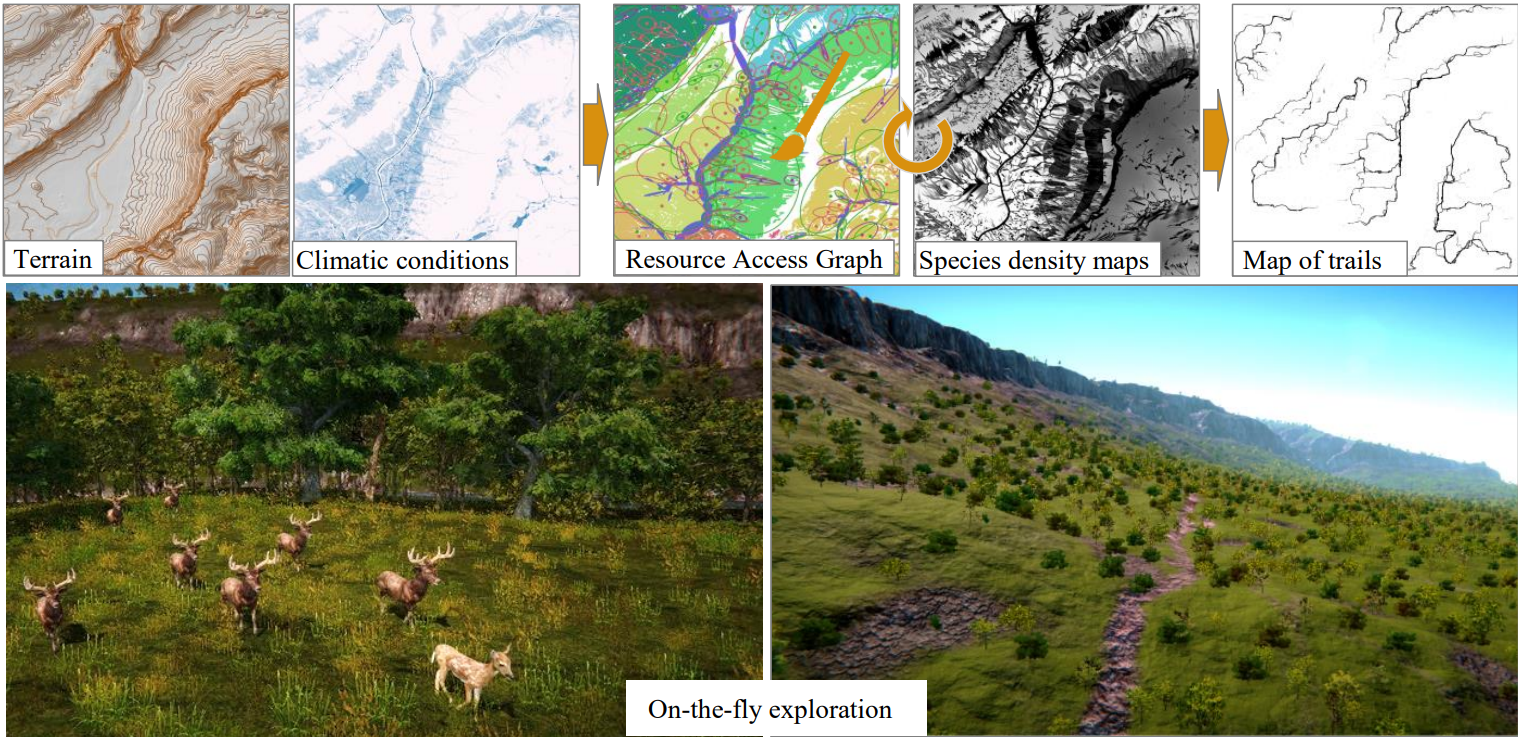
그림 1. 지형, 기후 조건과 경쟁 관계인 종 간 의도한 비율과 먹이 사슬 종속성을 입력으로 줌. 이 입력에 대해 우리의 알고리듬은 자원 접근 그래프에 대해 반복적으로 종의 밀도 맵을 계산하여 동물의 일상 경로를 추출할 수 있음. 그 결과로 식생, 동물, 그리고 동물이 만들어낸 경로를 전부 포함한 당장 사용 가능한 3D 지형이 나옴. 이 맵은 언제든지 페인트 툴로 수정 가능함.

이런 결과를 얻을 수 있는 이유는 몇 가지 중요한 점 위주로 선택을 했고, 근사를 했기 때문임. 첫번째 결정 사항은 각 먹이 사슬마다 종을 추가할 때 사용자가 이 비율을 직접 수정할 수 있다는 점임. 이때 이 입력으로부터 지형 위의 실제 표본의 개수와 분포를 얻을 수 있음. 이걸 구할 때 새로 만든 절차적 경쟁 알고리듬을 사용하는데, 이 알고리듬은 결과로 나온 생태계가 안전된 상태라는 가정이 있기에 간단하게 사용할 수 있음. 두번째 결정 사항은 자원 접근 그래프(RAG)라는 새로운 자료 구조를 기반으로 했다는 점임. 이 자료 구조는 각 종에 대응하는 자원을 위치와 접근성에 따라 계층적 그래프로 표현하여 효율적이면서 지형에 일관적으로 종의 개체화를 처리해줄 수 있음.

이 논문의 의의:

1. RAG라는 계층적, 생물학 기반의 자원 그래프로, 먹이 시슬 단계별 지역적 상호작용을 인코딩해주고, 자원 사이의 경로를 모델링할 수 있게 해줌.
2. 절차적 경쟁 알고리듬을 통해 각 먹이 사슬 단계 별로 안정된 상태의 생태계를 빠르게 근사할 수 있게 해줌.
3. 지형과 상호작용하면서 동시에 식물과 동물의 개체화를 일관적으로 수정할 수 있게 해줌.

2. 관련 연구

이 논문은 지형 생성에 집중하지 않음. 지형 생성이 궁금하다면 다음 논문을 참고: [Galin et al. 2019; Smelik et al. 2014].

식물 생태계는 대부분 자원의 경쟁을 시뮬레이션하는 방식으로 처리해왔음. Deussen et al. [1998]에서 처음으로 식물 경쟁 시뮬레이션을 통해 식물 분포를 처리했음. 최근에는 이 방식을 계층적 생태계로 확장한 논문이 있음[Makowski et al. 2019]. 최근에는 생태계와 다른 현상을 섞는 연구도 있음. Benes et al. [2011]에선 도시 환경과 식물이 자원을 위해 경쟁하는 현상의 상호작용을 인간의 도시 관리까지 고려하여 모델링해줌. Gain et al. [2017]에선 식물 분포를 시뮬레이션하고 학습해서 지형 위에서 상호작용할 수 있는 부쉬로 사용해줌. Cordonnier et al. [2017]에선 지형 침식과 식물의 상호작용을 모델링함. [Kapp et al. 2020]에선 입력 지형과 일관된 식생을 학습하고 생성하기 위해 심층 신경망을 학습시킴. 이 논문과는 다르게, 오로지 지형과 식물상의 상호작용만 고려했으며, 동물들이 식생과 침식에 주는 영향은 고려하지 않았음. 게다가 이 논문에서는 생존이라는 시뮬레이션 요소에 기반[Alsweis and Deussen 2005; Gain et al. 2017]하기에 지배적인 종에게 지역적인 우선 순위를 부여하지만 종의 비율을 제어할 수 있게 해주어 안정적인 상태의 생태계에 집중할 수 있게 해줌.

동물상에 대해서는 Reynolds의 연구[1987; 1999]에서 boids라는 개념을 소개함. Boids란 새 무리가 마치 한 몸으로 움직이는 것을 시뮬레이션해주는 것임. 애니메이팅한 에이전트의 속도[Paris et al. 2007; van den Berg et al. 2008]나 통합된 시야[López et al. 2019; Ondřej et al. 2010]를 기반으로 좀 더 세련된 결정을 할 수 있는 모델을 개발하여 관찰한 행동을 모방할 수 있게 해줌. 여기에 동물에 대해서 특히 환경과 동물이 상호작용을 하는 부분에 있어 예술적인 자유와 제어를 해줄 수 있도록 해주는 연구도 존재함. [Wang et al. 2014; Xu et al. 2008]와 같은 연구에서는 사용자가 동물의 그룹이 형성하는 모양을 제어할 수 있게 해줌. 동시에 Ecormier-Nocca et al. [2019]에서는 동물 무리를 모양 뿐만 아니라 분포까지도 제어할 수 있게 해줌. 이런 방법이 시각적으로 그럴 듯한 애니메이션을 제공하기는 하지만, 식생이나 지형의 접근성, 자원이 부족할 때와 같은 중요한 요소와의 관계를 고려하지 않음. 이걸 고려하는 것이 이 논문의 목표임.

식물상과 동물상에서 종 간의 경쟁은 생물학자들이 모델링을 해주었음. 이건 미분 방정식 등으로 표현이 되어있기에 예측이 가능한, 모집단의 생태학적인 틈새의 동적인 모델을 얻을 수 있으며, 전역 자원 관리에 대한 결정을 내릴 수 있게 해줌. 예를 들어 생태학을 위한 보존 생물학과 환경 분석 등에 영감을 받아 [Loreau 2010]에서는 생물다양성이 생태계에 갖는 영향을 보여주었고, [Shifley et al. 2017]에서는 숲 환경을 위한 동적 모델에 대한 종합적인 조사를 함. 우리에서는 동적 생태계를 시뮬레이션하는 방법을 제시하는 것은 아님. 대신 생태계의 일관성을 유지하면서도 실제의 자료를 기반으로 하든 가상의 자료를 기반으로하든 사용자의 입력을 받아들이는 경관을 생성하는 저작 도구에 집중하려고 함. 이렇게 유연하게 입력을 받을 수 있다보니 우리의 시스템이 완전한 통계적인 점유 모델이나 동물 모집단 다이내믹의 베이지언 시뮬레이션을 제공하려는 것이 아님. 광범위한 패턴과 점유 다이내믹에 대한 수학적 모델링에 대한 종합적인 인사이트를 얻고 싶은 독자들은 [MacKenzie et al. 2017]를 참고하면 될 듯.

3. 개요

이 논문의 목표는 아티스트/생물학자/고생물학자 등의 의도대로 식물상과 동물상이 경관에 일관적으로 존재하며, 생활하는 모습을 생성하는 것임. 여기서 사용자의 의도를 반영해주기 위해서 새로운 파이프라인을 제시함(그림 2 참고). 이 파이프라인을 통해 안정 상태 가설steady-state hypothesis 하에서 지형 위에 지형과 일관되게 식물, 초식동물, 육식동물을 생성하고 통합해줄 수 있음.

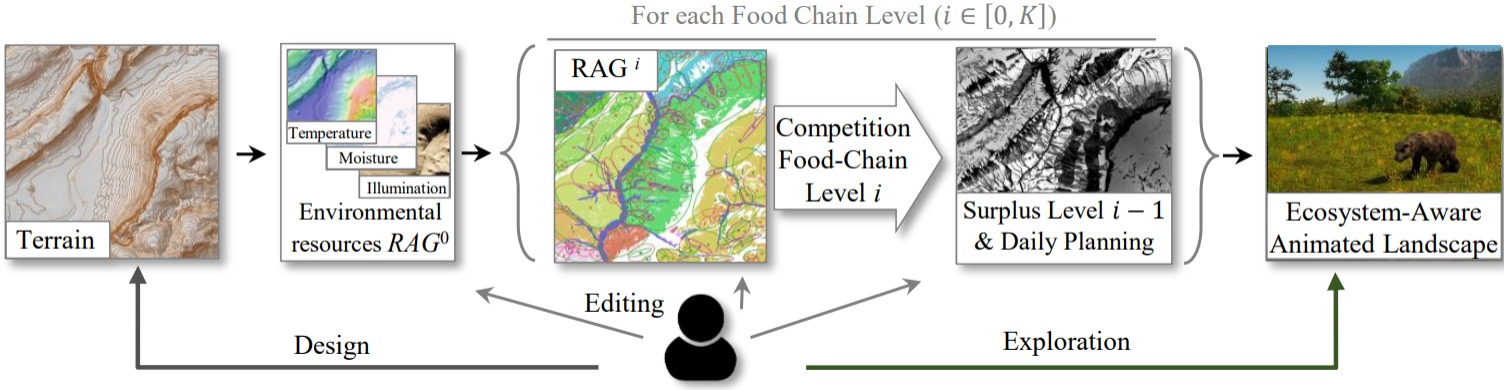
그림 2. 시스템 개요: 자원 맵을 초기화한 뒤 각 먹이 사슬 단계마다, 즉 식물에서 육식 동물까지 해당하는 단계에서의 자원 접근 그래프(RAG), 같은 단계 내의 종 간 경쟁의 결과, 동물의 일상 경로, 직전 단계의 자원의 남은 잉여를 계산함. 결과로 나온 밀도 맵과 지형에 대한 침식된 경로, 동물의 일상 계획을 통해 실제처럼 움직이는, 생태계가 존재하는 경관을 생성함. 사용자는 맵 위에 직접 그려줄 수 있어 직관적으로 맵을 수정할 수 있음.

안정 상태 가설이라는 제한 사항 덕에 생태계에서의 모집단의 성장은 두 가지 요소로 간단하게 볼 수 있음: 바로 자연사(노쇠사, 질병, 아사, 기후 등)와 포식임. 이게 없으면 각 종마다 자기 종의 고유한 성장률growth rate과 단위 당 종의 매년 평균 생산량(식물이 차지하는 부피와 신생 동물 등의 숫자 등)만큼 모집단이 매년 기하급수적으로 증가할 것임. 주어진 모집단의 연간 성장률yearly growth이란 모집단의 크기 곱하기 성장률임. 안전 상태 가설에 의해 매년 사망수가 생태계 내의 모든 종의 연간 성장을 보상해야함. 즉, 종의 연간 성장률만큼만이 다른 종의 자원으로 사용될 수 있음. 이러한 자원이 최종적으로 남아있는 연간량을 잉여surplus라 부르며, 이 잉여는 해당 연도에 자연사하는 양으로 간주함.

3.1. 지식, 입력 및 출력

이 논문에서 제시한 시스템에서 사용한 종에 대한 데이터는 식물 DB [Tela-Botanica DB]와 동물 DB [Animal-Diversity-Web DB]에서 가져옴. 이 데이터베이스에는 각 종마다 연간 필요로하는 자원(광물, 빛, 물(식물과 동물 둘 다) 등), 식물이 견딜 수 있는 최소 최대 기온, 동물의 평균 이동 속력, 경사면을 탈 수 있는지, 강 건널 수 있는지 여부 등에 대한 정보가 있음.

종이 필요로하는 자원들로 해당 종이 먹이 사슬 단계food-chain level에서 어디에 속하는지를 분류해줄 수 있음. 여기서 한 단계에 속하는 종은 그 직전 단계를 포식하며, 그 다음 단계의 먹이가 됨. 이 논문에서는 오로지 식생, 초식동물과 육식동물만으로 먹이 사슬을 분류하지만, 여러 단계로 우리의 논문을 일반화하는 것은 간단함. 7장에서 이 선형적인 구조를 먹이 그래프를 통해 좀 더 복잡한 생태계를 표현해주는 확장 방법에 대해서 논함.

사용자의 입력으로는 사용할 지형의 수치 표고 모델, 그리고 식물이 필요로하는 지역 환경 자원, 즉 광물minerals을 계산하기 위해 필요한 모든 필요 정보를 담은 광물 맵, 지형의 방위, 위도, 고도, 그리고 해수면에서의 극대/극소 기온, 즉 타겟 기후가 있음. [Gain et al. 2017]의 방법을 적용하여 해당 지형에 대한 연간 습도moisture, 극대소 기온extreme temperatures과 햇빛sun-light 맵을 추출함. 사용자가 물론 직접 이러한 맵을 제공해줄 수도 있으며, 생태계가 가질 종들에 대한 정보도 직접 제공해줄 수도 있음. 여기에 추가적으로 같은 먹이 사슬 단계에 속한 종들 간의 비율도 조정해줄 수 있음.

출력은 각 종마다 지형에 존재하는 밀도를 의미하는 맵들과 이들이 생성한 침식된 경로가 있음. 식물이 사용할 맵과는 다르게 동물에 대해서는 구분적으로 일정한 맵을 사용하여 종에 특정된 제한 구역confinement regions 내에서는 강이나 절벽처럼 동물이 건널 수 없는 자연적인 요소들을 제외하면 어디든지 움직일 수 있다는 점을 표현해줌. 보통 이 지역에서는 자원의 위치에 따라 무리가 비균일한 확률로 분포되어있기에 이들이 보통 선택하는 경로를 모델링하기 위해 일상표를 계산함. 이를 통해 다양한 종의 동식물이 존재하는 현실처럼 동작하면서 동물이 만들어낸 경로까지 반영한 경관을 생성할 수 있음.

3.2. 자원 접근 그래프 개념

우리 논문에서 제시하는 알고리듬의 핵심은 바로 자원 접근 그래프Resource Access Graph (RAG)라는 방향성 그래프 자료구조. 여러 먹이 사슬 단계에서의 종 간의 상호작용과 종과 지형 간의 관계를 인코딩해줌. 그림 3 참고.

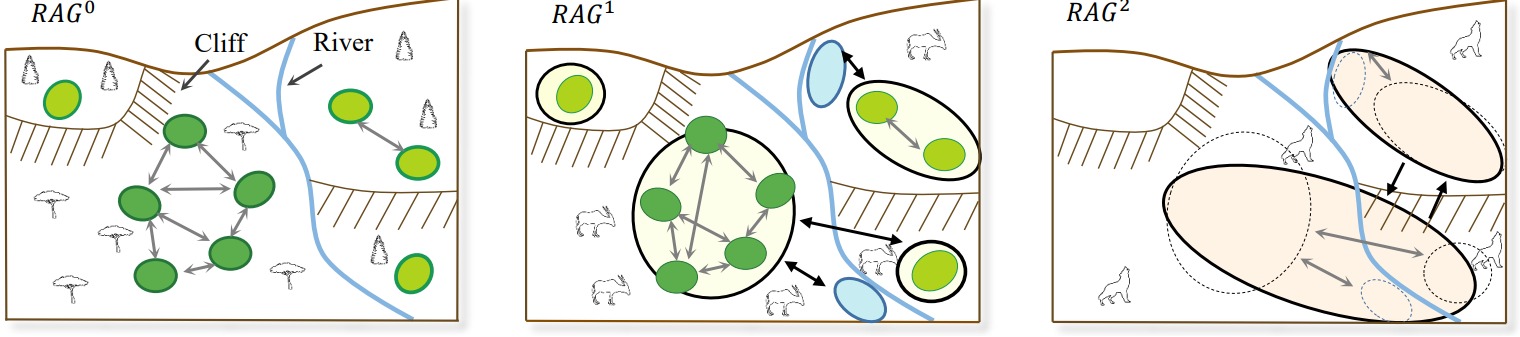
그림 3. 자원 접근 그래프의 개념도. 종 별 다른 색으로 잉여 노드를 구분함. RAG⁰에서는 식물이 필요로하는 자원을 인코딩함. RAG¹은 초식동물의 자원인 숲이나 강둑 등을 인코딩함. 영양은 강 여울에서만 강을 건널 수 있고, 절벽을 건널 수는 없기에 세 개의 제한 구역으로 나뉨. RAG²은 육식동물(늑대)의 자원(영양)을 인코딩함. RAG¹에서 연결된 성분들 중에서 영양이 잉여를 생산하는 부분(밑의 부분과 오른쪽 부분)은 RAG²에서는 하나의 자원 노드로 통합됨. 모서리를 통해 늑대는 절벽을 다른 이동 속도로 오르내릴 수 있음을 알 수 있음.

계층의 각 i번 단계에서의 RAG 노드는 i번 먹이 사슬 단계에 속한 종들이 사용할 자원이며, 그들의 지형에서의 위치임. 안정 상태 가설을 만족하기 위해 이전 먹이 사슬 단계에서의 잉여가 곧 자원이 되기에 생태계의 균형에 영향을 주지 않는 양만큼이 됨. 자원 노드는 곧 해당 자원이 맵 어디에 있는지, 그 영역을 의미함. 이름이 “자원 접근 그래프”이니 만큼 RAG 모서리는 종 별로 존재하며, 해당 종이 자원 노드 간에 이동이 가능한지, 그리고 평균 이동 시간이 어느 정도인지를 의미함. 여기서 그래프가 방향성인 이유는 경사진 곳을 올라가거나 내려가는게 서로 이동 시간이 다를 수 있기 때문임.

RAG의 계층을 통해 각 종이 곧 다른 종의 자원이 될 수 있음을 보일 수 있으며, 후자의 경우 더 윗 단계의 자원 노드가 됨. 즉, 큰 강과 절벽 사이의 지형 안으로 제한된 영양의 경우 늑대들의 먹이 자원이 되어주므로 영양들이 방목하려고 이동하는 RAG 간의 강력하게 연결된 성분이, 영양들이 잉여를 생산하기만 한다면, 곧 다음 단계의 RAG에서의 자원 노드에 대응하게 될 것임.

3.3. 처리 파이프라인

처리 파이프라인(그림 2)은 결국 RAG를 상향식으로 먹이 사슬 단계를 따라 계속해서 계산하고 갱신하는 것임. 직전 단계에서 얻은 종 간 경쟁과 위치에 따른 결과를 바탕으로 다음 단계를 계산함. RAG의 밀도 맵과 이동 모서리로 출력을 생성함.

좀 더 정확하게 설명하자면, RAG의 첫 단계인 RAG⁰(즉, 식물들의 환경 자원)에서는 각 맵의 셀을 하나의 노드로 간주하는 것으로 초기화해줌. 이후 다음 i번 먹이 사슬 단계마다 다음을 수행함:

1. 종들의 자원, 지형 위에서의 위치, 접근성을 인코딩해준 RAG와 연관된 단계를 생성함.
2. i번 먹이 사슬 단계에서의 경쟁을 절차적 방법을 통해 해결하여 사용자가 제공한 종 간 의도 비율에 가장 잘 맞는 안정 상태의 결과를 계산함.
3. 각 동물 종마다 자원 간의 일상 경로를 생성하며, 직전 먹이 사슬 단계에서 남은 자원을 바탕으로 잉여 맵을 생성함.

최종적으로 RAG의 경로를 최종적으로 다듬어주고, 하나로 합친 다음 지형 위에 침식된 경로로서 표기해주어 맵으로 출력해줌. 종 밀도 맵과 동물 종의 일상 경로를 처리하여 생태계를 생성하며, 잉여는 더 밀집되어있거나 더 높은 식물(종에 따라 다름), 더 젊은 동물 무리 등으로 표기하여 생태계가 살아있음을 보여줌.

사용자는 결과로 얻은 경관에서 임의의 먹이 사슬 단계의 밀도 맵을 수정해줄 수 있음. 어떤 한 종의 밀도를 너무 증가하게 되어 자원이 부족해진다는 상황이 발생하더라도 언제든 다시 줄일 수 있으며, 해당 수정 사항은 생태계 전체에 영향을 주어 일관성을 유지하게 해줌. 이러한 수정 사항은 화재나 질병과 같은 재난을 표현할 때 사용할 수도 있음.

4. 종 간 경쟁

같은 먹이 사슬 단계에 속한 종 간에는 자원을 두고 경쟁을 함. 처리 파이프라인의 두번째 단계에서는 종의 속한 여러 동물들이 현재 자기가 접근할 수 있는 자원이 주어졌을 때 지형 어디에 위치할지를 결정할 밀도 맵을 계산함. 사용자가 수정할 수 있게 해주기 위해 종 간의 목표 비율을 설정할 수 있게 해줌. 이 비율을 제공하지 않았다면 특정 자원에 가장 잘 알맞는 종이 해당 영역에서 더 잘 생존을 할 것임. 비율을 제공하든 하지 않든 어쨋든 모든 생존 조건을 만족하게 됨.

4.1. 적응도 제약

환경 및 생물학적 데이터베이스에서 얻은 정보 외에도 종과 자원에 대한 몇 가지 특징을 추출해 낼 수 있음. 우리 논문에서 사용하는 기능들은 다음과 같음:

어떤 종의 모집단 단위population unit란 동거하는 적은 수의 표본을 의미함. 식물의 경우 지형의 한 셀에서 존재할 수 있는 식물의 최소 밀집 그룹으로 정의함. 동물의 경우 가장 작은 일반적인 무리로 정의함. 무리란 다 같이 이동하는 동물 그룹으로 정의함. 혼자 돌아다니는 동물(곰 등)은 크기가 1인 무리로 간주함.

어떤 종 s와 어떤 자원 r이 주어졌을 때 소비 자원consumed resource c(s, r)이란 s의 한 단위가 매년 일반적으로 소비하는 r의 소비량을 의미함. 식물의 자원인 기온의 경우 이 값은 0이 됨. 식물이 기온을 소비한다고 해서 기온이 없어지는 것은 아니니까.

자원 r의 시간적 변화temporal variation [r_min, r_max]란 연간 소비 가능한 자원 r의 최소/최대량 사이의 시간 간격임(예를 들어 식물 입장에서는 기온차, 초식 동물 입장에서는 풀이나 숲의 연간 성장률의 변동). 계절 변화에 따라 달라지는 자원의 경우 데이터가 존재한다면 좀 더 구체적인 데이터를 적용함. 예를 들어 월간 기온 및 강수량 데이터를 사용하여 시간적인 변화를 줌.

각 종 s가 어떤 자원 r ∈ R(s)(s가 필요로하는 자원들)에 대한 적응도 범위fitness range란 폐구간 F(s, r) = [F_min(s, r), F_max(s, r)]을 의미하며, 이는 환경의 제한 범위 내의 종의 성장률에 대해서 자원 r의 최소 최대 값 사이의 구간을 의미함.

종 s의 제한 영역confinement region이란 지형 내에서 움직일 수 있는 범위를 의미함. 식물의 경우 이동할 수 없으므로, 동물의 경우는 절벽, 강, 혹은 과도하게 밀집된 숲에 의해 이동할 수 없는 경우 등에 의해 영역이 제한됨.

이러한 정의를 바탕으로 종 s의 한 모집단 단위는 자신의 제한 영역 내의 지역 자원을 바탕으로 생존을 해야함. s의 적응도 범위 내에서 매년 더 다양한 지역 자원들이 생존하면 할수록 이 지역에 더 많은 s가 거주하게 될 것임. 자연스레 이러한 구간이 겹치지 않는다면 거주가 불가능할 것임. 마지막으로 s의 모집단 단위는 오로지 각 자원의 연간 c(s, r)량이 충분히 남아 소비할 수 있을 때만 새롭게 생성됨. 이 논문에서는 이러한 제약 사항을 지속적으로 만족하여 생태계의 일관성을 보장함.

4.2. 지역 종의 적응도 점수

한 먹이 사슬 단계에 속한 종들이 소비할 수 있는, r ∈ R인 자원 r이 어떤 영역에 존재한다고 가정. 이때 종들 중 누가 이 자리를 차지할 확률이 높느냐를 계산할 땐 적응도 점수fitness score fit(s, R)을 사용함.

각 r ∈ R인 자원 r들에 대해 종의 적응도 범위 F(s, r) 중 주어진 자원 r의 연간 변화량 r_year에 해당하는 범위를 계산함. 가장 드문 드문 난 자원이 s가 그곳에 거주할 수 있는지 여부를 결정할 수 있으므로, 최소값을 사용해주면 됨:

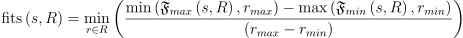
월간 시간적 변화도 주어진다면 위의 최소값에 자원별로 여러 항들을 사용해주면 됨. 위의 식의 결과는 0 <= fit(s, R) <= 1인 연속된 값이 나옴. 0이면 s가 생존이 불가능하다는 것이고, 1이면 제일 적응도가 높다는 것임. 어쨋든 모든 자원의 변화량은 종의 적응도 범위 내에 있음.

4.3. 경쟁 알고리듬

지형을 여러 제한 영역 C로 나누었다고 가정. 이때 각 제한 영역 C_j에 대응하는 자원 집합을 R_j으로 표기. 이때 q(r, C_j)은 r ∈ R_j인 C_j 내의 자원 r의 연간 소비 가능한 자원량을 의미.

참고로 종별로 영역이 달라지지는 않음. 종 간 이동 가능성이 달라지면 서로 이동 능력이 다른 종 간의 제한 영역 간의 교집합을 새로운 제한 영역으로 만들어줌. 이 경우 생성된 모집단 단위는 해당 종의 본래 제한 영역에 할당함.

종의 목표 비율을 고려한 경쟁. 지형에서 밀도가 0일 때 시작해서 연속적으로 각 종의 모집단 단위의 개수만큼 증가시킴. 이 논문에서는 탐욕적인 방법을 사용해서 여러 방법 중 가장 의도 비율과 맞는 단 하나의 방법을 선택하도록 함. 새롭게 생성된 단위는 가장 적합한 제한 영역 C_j에 할당해줌. 즉, 오로지 순양수인 fit(s, R_j)을 갖는 C_j만을 고려하며, 이러한 C_j에 대해서 내림차순으로 정렬했을 때 첫 원소를 사용함. 즉, ∀r ∈ R_j, q(r, C_j) > c(s, r)임. 만약 이게 성공한다면 모집단 단위를 C_j에 추가해주며, r ∈ R_j인 자원 r마다 q(r, C_j)의 값은 c(s, r)만큼 감소함. 더 이상 새로운 모집단 단위를 추가해줄 수 없을 때까지 이 과정을 반복함.

알고리듬 1: 목표 비율에 따른 경쟁 알고리듬

FCL은 Food Chain Level, 즉 먹이 사슬 단계를 의미

• 입력: 각 s ∈ FCL인 종 s와 s가 갖는 비율
• 출력: 각 s ∈ FCL 별 밀도 맵
• 반복
  • FCL을 가장 목표 비율과 가깝게 만들어줄 s를 선택
  • s의 각 제한 영역 C마다 fit(s) 계산
  • 가장 적응도가 높은 C 선택
  • C 내의 s의 밀도 증가
  • 이에 따라 C 내에서 소비 가능한 자원량 감소
• 자원이 충분하지 않아 더 이상 밀도를 증가할 수 없을 때까지

목표 비율 없는 경쟁. 각 제한 영역 C_j마다: 0부터 시작해서 ∀r ∈ R_j, q(r, C_j) > c(s, r)을 만족하는 순양수 적응도 fit(s, R_j) 중 최대값을 갖는 종에 대해 모집단 단위의 수를 반복적으로 증가시켜줌(이에 따라 당연히 소비 가능한 자원량도 감소). 더 이상 C_j에 소비 가능한 자원이 충분하지 않을 때까지 진행.

알고리듬 2: 목표 비율이 없는 경쟁 알고리듬

• 입력: 각 s ∈ FCL인 종 s
• 출력: 각 s ∈ FCL 별 밀도 맵
• 반복
  • 각 제한 영역 C (혹은 그 교집합) 마다
    • s의 각 제한 영역 C마다 fit(s) 계산
    • 가장 적응도가 높은 C 선택
    • C 내의 s의 밀도 증가
    • 이에 따라 C 내에서 소비 가능한 자원량 감소
  • 종료
• 자원이 충분하지 않아 더 이상 밀도를 증가할 수 없을 때까지

논의. 비대칭 경쟁과 적응도 점수와 같은 식물 생태계에 해당하는 개념들[Alsweis와 Deussen 2005; Gain et al. 2017]을 물론 세부적으로는 적용해주고 있기는 하지만, 우리 논문에서는 해당 방법들이 생태계 시뮬레이션 방법에 속하지 않기에 써주지 않음. 식물 씨 뿌리기, 성장, 죽음, 동물의 탄생, 노화, 죽음 등을 시뮬레이션해주지는 않음. 우리 방법은 지역 경쟁에 집중할 뿐임. 물론 샌드박스 시뮬레이션처럼 종 간 정확한 비율을 물론 입력해줄 수는 있겠지만, Ecobrush[Gain et al. 2017]와 같은 방법에서 우리의 정확한 식물 배치 방법을 차용하여 그들의 페인팅 균일 분포에 사용해줄 수 있을 것임. 심지어 식생만 고려하더라도 이 식물이 어느 위치가 제일 발전하지 좋은지 여부를 고려하기에 좀 더 다양하면서도 지형에 일관된 결과가 나올 것임.

모집단 단위가 고정된 크기의 단위로 생성된다면, 목표 비율에 가장 잘 맞는 단순한 결정적 알고리듬이 정확한 해답을 언제나 주는 것은 아님. 게다가 생존 제약들이 강제되기 때문에 현실적이지 않은 입력에 대해서는 상당히 드문 드문 존재하는 생태계가 만들어져 자원의 잉여가 매우 커질 것임. 그렇지만 이 알고리듬은 일관성은 유지하면서도 반복적으로 목표 비율까지의 거리를 줄인다는 장점이 있음. 두번째 알고리듬은 영역 기반 전략을 사용하므로 지역 자원 잉여를 반복적으로 줄여줄 수 있음. 물론 후자도 모집단 단위의 크기에 따라 0으로 수렴하지는 않을 수 있음. 결과적으로 입력으로 제공한 종만 제대로 정의했다면, 다양한 생태계가 생성될 것임. 동물이 무리로 생성된다는 점과 식생이나 하위 종에서 추가적인 잉여가 남는 점에서 좀 더 현실적이 있다고 볼 수 있음.

탐욕적 알고리듬을 사용하기는 하지만, 두 해법 다 각 먹이 사슬 단계마다 일반적인, 상대적으로 적은 수의 종이 주어졌을 때 지형의 각 영역마다 소비 가능한 자원을 전부 고려하여 지역적으로 종이 명백히 나뉘는 영역이 생기는데, 이를 전부 계산하는 것이 효율적이라는 장점이 있음.

4.4. 출력: 종 밀도 맵

경쟁이 끝나면 각 그리드 셀마다 식물종의 지역 밀도를 지형의 표면을 식물이 가리는 정도에 비례하도록 해줌. 동물의 밀도의 경우 각 종별 제한 영역에 대해서 제곱미터당 표본의 수로 정의함. 밀도는 흑백의 정도로 표기하여 동물종 맵을 구역별로 균일한 색으로 표기해줄 수 있음(그림 4(c) 참고).

결과적으로 얻을 수 있는 맵은 사용자가 손쉽게 알아볼 수 있도록 하여 맵에서 어느 영역이 가장 인구밀도가 높은지, 혹은 어떤 종이 어떤 구역에서 제일 많은지 등을 알아 볼 수 있음. 이렇게 직관적으로 보기 좋게 시각화했다는 점에서 그리기 툴 등으로 수정하기 쉽게 만듦.

5. 상향식 RAG 계산

여러가지의 맵을 직접적으로 먹이 사슬을 따라 유형, 수량, 종의 이동 능력과 자원으로의 접근성, 물에 대한 수요, 다른 종에 대한 포식을 확인해주면서 진행하는 것은 좋은 해결방법이 아님. 데이터 계산을 단순화하고 위와 같은 정보에 대한 탐색을 좀 더 효율적으로 만들기 위해 필요한 모든 정보를 추출하여 그래프 구조로 계층적으로 표현해줌. 즉, 그림 3에서 이미 소개한 자원 접근 그래프(RAG)를 사용함. 5장에서는 RAG에 대한 형식적인 정의를 소개하고, 이 구조를 어떻게 점진적으로 구축하는지를 소개함.

먹이 사슬을 표기해주기 위해 다음과 같은 표기법을 사용하도록 함: 생태계 내의 종은 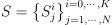으로 표기하며, 여기서 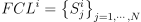는 먹이 사슬 단계 i의 종을 의미하는 부분 집합임. 이 논문에서는 FCL⁰이 식물, FCL¹이 초식동물, FCL²이 육식동물을 의미함. Rⁱ는 FCLⁱ이 필요로하는 자원 집합을 의미함. 이러한 자원들은 공간적으로 표기함: r ∈ Rⁱ인 자원 r은 근본적인 속성과 사용 가능한 수량 뿐만 아니라 해당 자원이 커버하는 범위(예를 들어 이 논문에서는 무한하다고 가정한 수자원의 경우 동물이 목을 축일 수 있는 강둑 등의 범위를 커버함)로도 표기함. 자원 접근 그래프(3.2 섹션 참고)는 다음 원소를 이용하여 생성함.

자원 노드resource node v는 RAG의 정점임. 어떤 한 위치에 속한 하나 이상의 자원을 의미함. 자원 노드 V는 해당 자원이 지형에서 차지하는 영역의 중심에 위치함. 노드는 먹이 사슬 단계에 따라 계층순으로 정렬함. 자원량quantity of resource q(r, v)은 v에서 소비 가능한 자원 r의 자원량으로, 자료구조의 노드에 각 자원별로 저장이 되어있음.

공간 모서리spatial edge e는 RAGⁱ의 두 노드를 연결하는 방향성 모서리임. s ∈ FCLⁱ인 종 s별로 라벨링이 되어있으며, 지형 위에 두 노드 간에 s가 이동할 수 있는 경로가 존재함을 의미하게 됨. 모서리의 값은 각 방향별 이동 시간임.

계층적 모서리hierarchical edge h는 단계간 모서리로, RAG^{i + 1}의 노드(예를 들어 늑대의 자원인 영양의 무리)와 RAG^{i + 1}를 만드는데 사용한 RAGⁱ의 노드(즉, 앞에서 언급한 영양 무리의 자원)를 이어줌. 계층적 모서리를 통해 영양 무리가 정확히 어느 영역에 있고, 어느 경로에 있는지 등, 해당 자원에 대한 정보를 얻을 수 있음.

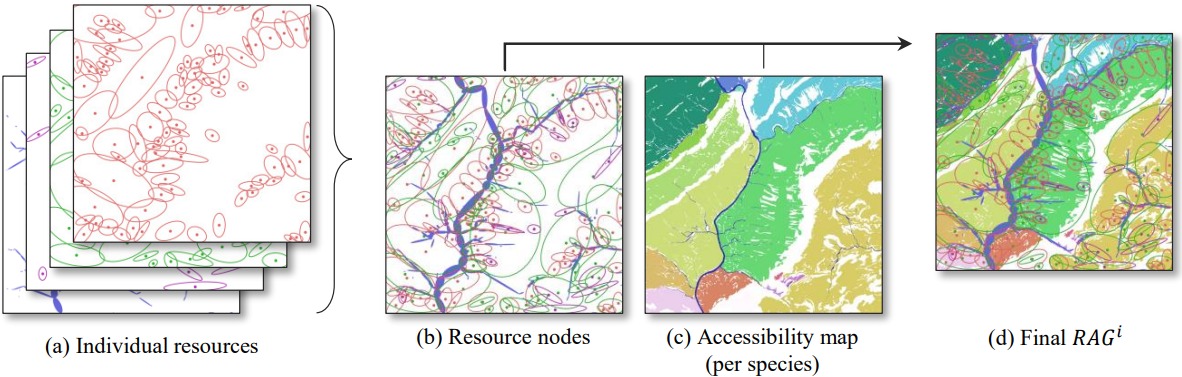
그림 4. RAGⁱ: 공간적 자원 (a)가 종 자원 노드 (b)로 변환되며, 접근성 맵 (c)을 구함. (c)의 같은 색에 속한 노드들은 최종적으로 종으로 라벨링한 모서리로 연결됨 (d). 임의의 모양으로 된 영역이 존재는 하나, 공간적 자원을 자원의 색, 크기, 위치가 각각 근본적인 속성, 양, 자원의 중심에 대응하도록 타원으로 묘사함으로써 현저성을 향상시킴.

5.1. RAG 초기화: 식생 및 접근성 맵

RAG⁰은 식물이 필요로하는 자원을 모델링한 것임. 즉, 3.1 섹션에서 보여줬던 것처럼 입력 토양 유형과 지형 위의 그리드의 기후에 따라 계산함. 각 그리드 셀의 중심마다 노드를 생성해서 해당 지역의 자원에 대한 정보를 저장함. 4 섹션에서 소개한 경쟁 알고리듬을 사용하여 RAG⁰을 바탕으로 FCL⁰(식물상)에 대한 밀도 맵을 계산함. 참고로 식물은 그리드 셀의 자원에 종속되어있기 때문에 그래프 간의 연결이 없음(역자: 식물은 안 움직이니까 ^_^…).

식물 종마다 인공적으로 공간 모서리를 RAG⁰에 추가해주어 같은 종이 자라는 이웃 자원 노드를 연결해줌. 이를 통해 특정 식물 종이 자라는(예를 들어 풀숲 등) 영역을 하나의 초식 동물의 자원으로 간주하여 RAG¹의 한 노드로 그룹화해줄 수 있음.

마지막으로 지형을 전체 동물상에 대해 제한 영역으로 구분해줌. 좀 더 정확히 말하자면, 어떤 동물 종 s에 대한 접근성 맵accessibility map을 구하라는 의미임: 우선 일반적인 그리드로 초기화를 해주는데, 이때 s가 지나갈 수 없는 장애물(예를 들어 종 별로 그 정도는 다르겠지만, 수심이 깊은 물, 가파른 경사면, 우거져서 밀도가 과도하게 높은 식생 등)을 갖는 셀은 따로 표기를 해줌. 이후 반복적으로 플러드 필 알고리듬을 사용하여 나머지 셀 중 연결된 성분을 계산해줌. 그림 4(c)의 경우 장애물은 하얀색으로 표기했으며, 다른 영역은 각자 고유한 색으로 칠해져있음.

5.2. RAGⁱ와 FCLⁱ 밀도 맵으로부터 RAG^{i + 1} 생성하기

자원 노드와 계층적 모서리. RAG^{i + 1}은 동물의 자원 그래프를 의미함. 우선 물 노드(예를 들어 동물이 물을 마실 수 있는 호숫가, 강가 등)를 만들어줌. 이후 RAGⁱ의 정보를 사용하여 FCLⁱ(동식물)이 한 지역에서 소비 가능한 먹이 당 노드 하나를 추가해줌:

s_jⁱ ∈ FCLⁱ인 각 종마다 s_jⁱ이 존재하는 노드와, 이 종에 대하여 라벨링된 공간 모서리에 대하여 RAGⁱ가 주는 제한 사항에 대하여 고려해봐야함. 우선 FCLⁱ에서의 경쟁을 통해 얻은 s_jⁱ의 밀도 맵(4 섹션)을 통해 해당 종의 존재성을 우선 확인해줌. 이 방향성 부분 그래프의 강한 결합 성분이 곧 이제는 자원의 역할을 하는 s_jⁱ이 소비 가능한지를 의미함. 그러므로 이제 각 강한 결합 성분을 v ∈ RAG^{i + 1}인 하나의 노드 v로 합쳐주어 이 자원을 표기해줌. v와 관련된 영역(예를 들어 식물이 차지하는 영역 혹은 동물 무리가 서식하는 제한 영역 등)을 s_jⁱ의 밀도 맵으로부터 얻어냄. 생태계의 안정 상태를 보존하기 위해 소비 가능한 자원량인 q(r, v)를 해당 영역에서 s_jⁱ의 연간 생장률(지역 표분의 수와 종의 생장률을 곱한 값)로 해줌. 최종적으로 v를 정의할 때 사용한 RAGⁱ의 노드를 v와 연결해주어 계층적 모서리를 생성해줌.

공간 모서리. 공간 모서리는 FCL^{i + 1}의 동물 종 s_j^{i + 1}에 대해 라벨링을 해줌. s_j^{i + 1}와 같은 제한 영역에 존재하는 모든 노드(그림 4(b)에서 타원의 중심), 즉 접근성 맵에서 s_j^{i + 1}와 색이 같은 점 한 쌍에 대하여 두 방향 모두 연결해줌으로써 생성함.

마지막으로 각 방향성 모서리 (v₁, v₂)마다 i와 j가 종을 의미할 때 이동 시간 tⁱ_j(v₁, v₂)을 계산해줌: 지형 그리드에 대해서 최단 경로 알고리듬을 수행하여 v₁에서 v₂으로의 최단 경로를 구해줌. 이때 경사와 종의 이동 능력도 고려해줌. 종이 건널 수 없는 수준의 경사를 갖는 그리드와의 모서리는 경로 구하기 전에 삭제해주며, 그 길이(이동 시간)를 경사를 바탕으로 구해줌. 이렇게 되면 지형의 위상을 고려한 곡선 경로가 나오게 됨. 참고로 이 최단 경로와 이 경로에서의 이동 시간은 방향마다 다룰 수 있음(보통 동물들은 경사가 가파른 곳을 내려가는 건 가능한데, 다시 올라가는 건 불가능함). tⁱ_j(v₁, v₂) 값을 통해 무리의 일상 일정을 계획하는데 RAG 계층을 사용해줄 수 있음. 각 동물을 개체화할 때 좀 더 세밀한 경로를 구해야하므로 좀 더 구체적인 이동 속도를 사용해줌.

6. 생태계를 고려한 경관

6.1. 침식된 경로 맵

보통 동물은 시야에서 잘 보이지 않기 때문에, 동물이 어떤 한 지역에 존재함을 아는 가장 첫번째 흔적은 동물이 남긴 경로임. 그러므로 생태계를 3D로 개체화하기 전 동물들이 그린 경로를 생성해준 다음, 해당 경로의 사용 확률을 누적한 값을 통해 침식을 적용해줌. 이는 각 동물이 자신의 제한 영역 내의 각 RAG 노드마다 얼마나 시간을 보냈는지를 바탕으로 공간 모서리에 동물상이 있을 확률을 구해주고, 이 모서리를 경로로 좀 더 세밀하게 표현해주는 것으로 구현해줄 수 있음.

어떤 종 s의 한 무리 h가 영역 C에 제한되어있다고 가정. h가 어떤 한 자원 노드 v에 존재할 확률은 r ∈ R(s)인 해당 자원에 대한 s의 필요성과 소비 가능량 q(r, v)에 달려있음. s 종의 동물이 C 내의 RAG 노드에 대해서 균일하게 r을 소비하며, 무리가 r에서 머무를 시간은 r에 대한 연간 소비량 대 s가 필요로하는 전체 자원량 c(s, R(s))의 비율에 비례한다고 가정했을 때 s가 v에 있을 확률은 다음과 같음:

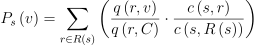
(1)

여기서 q(r, C)는 영역 C에서 소비 가능한 r의 총량임.

이제 C의 두 RAG 노드의 공간 모서리 (v, v’)에 대해서 무리가 이곳을 이동할 확률을 구할 시간. 이 모서리의 값인 근사 이동 시간 t_s(v, v’)을 통해 무리가 이 직빵 경로를 사용할 것인지, 아니면 다른 자원 노드를 경유할 것인지를 알 수 있게 됨. 그러므로 v에서의 무리가 공간 모서리 (v, v’)를 확률인 P_s(v’|v)를 v’로 갈 확률에 직빵 경로 이동 시간의 역(더 긴 경로는 덜 사용될 것이므로)만큼 가중치로 준 값을 다른 자원으로 갈 확률에 가중치를 마찬가지로 곱한 것들의 총합으로 나눈 것으로 구할 수 있음:

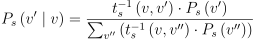
(2)

종 s가 C 안의 v와 v’ 간의 경로에서의 침식에 얼마나 영향을 주느냐는 연간 해당 공간 모서리를 이동한 표본의 질량의 총합에 비례함. 식 1과 식 2에서 구한 확률과 C에서의 표본수 ||s||와 평균 질량 m_s를 사용하여 구할 수 있음:

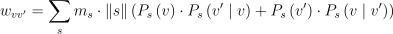
(3)

여기서 w_vv’는 v에서 v’, 그리고 v’에서 v로 이동한 동물들의 무게의 누적임.

이제 RAG 그래프를 무방향으로 간주한 다음, 각 모서리의 값을 w_vv’로 주어 침식된 경로 맵을 계산함. 우선 가장 w_vv’ 값이 높은 모서리인 지형 위의 최단 경로로 침식 경로를 초기화해준 다음, 반복적으로 지형과 RAG에서 각 모서리의 끝에서 w_vv’ 값이 높은 모서리를 선택하여 확장을 해줌. 이때 경로 중에서도 가장 긴 연속된 루트를 가장 자주 사용하는 것부터 시작해서 스플라인 곡선을 활용하여 부드럽게 만들어줌. 모든 RAG 모서리를 처리해줄 때까지 이 과정을 반복함. 결국 경로는 트리 혹은 그래프 구조가 되게 됨. 그림 5(좌측)에서 볼 수 있듯, 각 부분의 색의 강도가 곧 해당 경로의 사용 빈도를 의미하며, 무게에 비례하도록 설정했음. 참고로 실제 자연 지형에서도 몇가지 주요 경로가 존재함. 즉, 동물들 입장에선 어떤 지역에 자원이 풍부하다거나 환경 자체가 그곳으로 가도록 강제하기 때문에 같은 위치로 계속 가게 됨. 동물들은 이 주 경로에서 여러 자원들로 퍼져나가게 됨.

이 경로를 실제 렌더링을 해줄 때 시각적으로 표현해주기 위해 이 경로를 식물 밀도 맵에서 빼주며, 가중치에 따라 살짝 지형을 깎아준 뒤 약간 진흙이나 암석 등의 텍스처로 렌더링해줌.

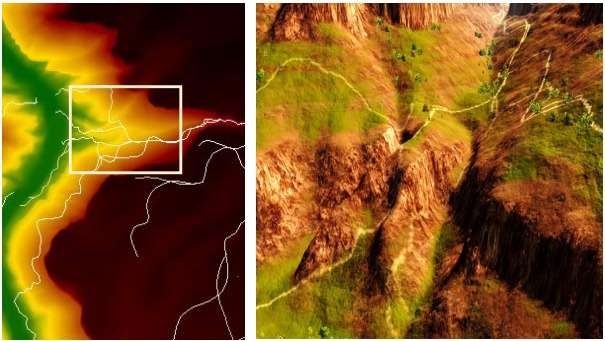
그림 5. 동물 경로 및 맵(좌측)과 3D 탐험을 위해 선택된 영역(우측). 이 예시는 그랜드 캐니언 DEM을 사용했음. 이를 통해 경로가 어떻게 분기하여 좌우로 진행할 뿐만 아니라 계곡 아래로도 내려가는지를 보여줌.

6.2. 3D 일상 계획 및 동물 개체화

종 s의 한 무리 h의 일상 계획daily-planning이란 무리의 제한 영역의 RAG 노드를 방문한 순서대로, 그 노드와 노드에 들어오고 나간 시간에 대한 정렬된 리스트 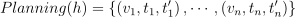임. 무리 별로 이러한 계획을 계산하는 것이 3D 개체화의 핵심임.

무리 h가 하루에 얼마나 많은 자원 노드를 연속으로 방문할 수 있는지를 계산해주기 위해 RAG의 공간 모서리의 근사 이동 시간 t_s(v, v’)을 통해 주어진 노드에서 얼마나 오래 있는지를 추정함. 실세계에서는 한 무리가 실제로 한 자원에 얼마나 시간을 할애하는지는 각 종마다 갖고 있는 복잡한 법칙을 따를 것이지만, 이 논문에서의 방법은 그러한 특수한 동물학적 지식을 사용하지는 않음. 대신 해당 노드에 대한 종의 수요와 자원량(연간 성장률에 비례함)에 따라 평균 방문 시간 t_s(v)을 추정함.

한 순간에 너무 많은 동물이 같은 위치에 있을 수도 있으니, 이를 방지하기 위해 이 논문에서 사용하는 준 무작위 계획 알고리듬에서는 한 노드가 커버 가능한 동물의 최대 개수(이 논문에서는 해당 값을 노드의 영역에 비례해서 적용함)를 의미하는 노드 용량node capacity이라는 개념을 사용함. 또한 종 별로 매일 반드시 방문해야하는 필수 자원(물 등)에게 우선순위를 부여함.

이 전체 과정은 알고리듬 3에서 요약해두었음. 이 과정 자체는 다음과 같음: 시간 T가 0일 때, Planning(h)를 빈 리스트로 초기화를 한 다음, 리스트 인덱스 j를 1로 둠. 필수 자원에 우선순위를 준 다음, 무작위로 자원 r을 뽑은 뒤, P_s(v) 혹은 리스트에 v_{j - 1}가 존재한다면 P_s(v_{j - 1} | v)의 확률에 기반해서 r이 존재하는 노드들 중 다른 무리들에 의해 이미 가득 차지 않고 공간이 남은 가장 확률이 높은 노드 v를 선택함. 선택한 후에는 선택한 노드 v의 용량을 현재 무리의 크기만큼 빼주고, 현재 시간 T를 t_s(v_{j - 1}, v)(v에 도착함)으로 업데이트해준 다음 Planning(h)에 새 노드 j인 (v, T, T + t_s(v))를 추가함. 다시 시간 T를 T + t_s(v)(v에서 떠남)로 업데이트 해준 다음 전체 과정을 반복함. 시간이 종이 깨어있을 시간을 초과하기 전까지 계속해서 반복함.

알고리듬 3: 종 s의 무리의 일상 계획 알고리듬

• 입력: 종 s ∈ FCLⁱ, RAGⁱ, ∀r, t(s, r)인 종 s의 무리들
• 출력: 종 s의 모든 무리의 일상 계획
• 종 s의 각 무리 h 마다
  • Planning(h) ← ∮; counter ← 0; j ← 1;
  • r을 c(s, r)의 중요도를 내림차순으로 정렬
  • 반복
    • 만약 필수면서 아직 다루지 않은 어떤 r이 존재할 때
      • 확률분포 P_s(v)로부터 r을 포함하는 소비 가능한 v ∈ RAGⁱ를 표집
    • 존재하지 않을 경우
      • P_s(v)로부터 아무 소비 가능한 v ∈ RAGⁱ를 표집
  • 종료
  • v_j ← v; t_j ← counter; t_j’ ← counter + t_s(v);
  • Planning(h) ← (v_j, t_j, t_j’);
  • v_j에서 사용 가능한 공간을 감소
  • counter ← counter + t_s(v) + e_s(v_j, v_{j - 1});
  • j ← j + 1;
  • counter > 종 s의 활성일의 길이일 때까지
• 종료

일상 계획은 먹이 사슬을 따라서 구하기 때문에 위에서 구해준 v의 위치는 육식 동물들 입장에서는 현재 육식 동물이 추적 중인 무리의 현재 위치를 그들의 계획을 바탕으로 구하여 해당 위치로 v를 바꾸게 됨. 이를 통해 육식 동물이 초식 동물의 무리를 따라가는 것처럼 해주어 상당히 일관적인 상호작용을 적용해줄 수 있음. 그림 7의 윗부분 참고.

알고리듬을 통해 구한 일상 계획 노드를 무리의 경로의 중간 목표로 사용해줌. 기존에 자원 간의 이동 속도를 추정하기 위해 구했던 경로 정보를 다시 갖고 와서 스플라인 곡선으로 하나로 만들어주고, 다듬어주어 더 부드러운 결과를 만들어줌. 각 무리가 무리의 경로를 통해 움직이는 속도는 종의 동물학적 속성에 따라 정함.

사용자가 직접 수정을 해줄 땐 결과를 2D 맵 위의 무리들의 움직임으로 표기해줌. 사용자는 자원을 클릭하여 경로를 수정해줄 수 있음. 이렇게 시각화를 해주는 것으로 사용자가 빠르게 탐험하고 싶은 영역을 빠르게 선택할 수 있게 해줌.

탐험 도중엔 카메라의 위치와 시야각에 따라 동물을 그때 그때 바로 개체화해줌. 동물은 Reynolds [1987]의 알고리듬을 사용하여 애니메이션해주어 충돌을 막고, 무리 간의 관계를 반영한 움직임을 반영해줌. 참고로 이 논문에선 이 단순한 방법을 사용해도 이 논문의 핵심을 3D로 시각화하기엔 충분하였기에, 종 별로 종 특유의 무리 짓는 모습을 반영하지 않아 Ecormier-Nocca et al. 2019 개선할 수 있는 부분이 있음.

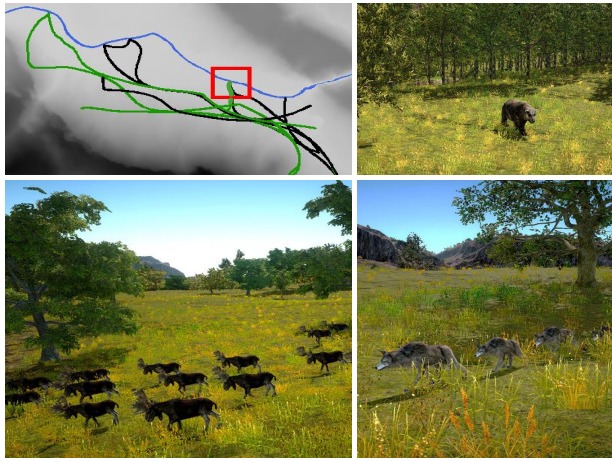
그림 7. 왼쪽 위: 말코손바닥사슴 무리의 일상 계획(초록색)과 이들을 추적하는 늑대 그룹(검은색). 이 둘은 강가에 같은 시간에 도착하며(빨간색 사각형) 늑대는 하루의 나머지 시간동안 다른 무리를 쫓음. 오른쪽 위와 아래: 곰, 말코손바닥사슴과 늑대가 자신의 일상 경로를 지나는 모습.

7. 결과 설명 및 논의

7.1. 구현, 성능 및 결과

7.2. 검증

7.3. 이용자 연구

7.4. 한계 및 논의

검증을 통해 우리 방법의 일관성과, 일관적이고, 애니메이션이 적용된 경관을 보장하면서도 시간을 절감할 수 있다는 그 잠재성에 집중하기는 했지만, 몇 가지 한계가 있음.

위에서도 강조했듯이, 우리의 모델은 근본적으로 종 간의 동적인 경쟁을 모델링할 수 없음. 게다가 우리의 절차적인 해법은 오로지 안전 상태 생태계를 근사함. (예를 들어 만약 잉여가 먹이 사슬을 따라 완전 소비된다면 자원으로서의 역할을 하는 종은 해당 년도에 아무도 자연사하지 않을 것.) 그렇기에 실제 결과가 얼마나 현실적이느냐는 사용자가 종 간의 비율을 얼마나 적절히 주느냐에 달림.

또한 현실에서 고려해야할 요소 몇 가지를 무시함. 새, 크기가 작은 동물 종, 해양 자원 등을 포함한 더 크고 복잡한 먹이 사슬을 고려해야 더 완전한 생태계를 만들 수 있었을 것임. 이걸 고려하려면 분기가 있는 먹이 사슬로 방법을 확장해야함. 다행히 구현은 간단함. 어차피 계산 자체는 계층적으로 그대로 이루어질 수 있으니까. 생성된 경관도 여러 방법으로 좀 더 현실성 있게 만들어 줄 수 있음. 예를 들어 큰 동물들의 경로 근처에 있는 나무에 피해를 준다거나 등. 무엇보다도 종 간의 상호작용을 모델링해준 방법 자체에 아직 한계점이 있음. 종 간의 협업을 고려하지 않음[Courchamp et al. 2008]. 예를 들어 식생의 꽃가루매개충이나 동물상의 배변 활동을 통해 땅이 비옥하게 되는 현상 등. 이런 협업을 구현하려면 먹이 사슬에 루프가 생겨야 하는데, 이건 우리의 파이프라인이 처리해줄 수 없음. 그나마 가능성 있는 해법으로는 사용자가 수정 중일 때 하위 단계에 계산된 맵을 다시 넣어주는 것임. 예를 들어 그림 13의 빙하기에서의 동물 밀도의 합을 계산한 맵을 다시 식생을 위한 입력 자원으로 넣어준다면 동물상이 적은 지역에서는 후자가 좀 더 드문 드문 존재할 것임. 그림 15 참조. 하지만, 대신, 새 식생 맵은 동물에 영향을 주기에 이 과정을 반복해줘야 함. 이러면 동적인 생태계가 발생함. 물론 수렴한다는 이론적인 보장은 없음.

8. 결론 및 향후 연구

감사의 글

참고문헌

M. Alsweis and O. Deussen. 2005. Modeling and Visualization of symmetric and asymmetric plant competition. In Eurographics Workshop on Natural Phenomena

Animal-Diversity-Web. DB. https://animaldiversity.org/. Accessed: 2020-01-22.

Bedrich Benes, Michel Abdul Massih, Peter Jarvis, Dadniel G. Aliaga, and Carlos A. Vanegas. 2011. Urban Ecosystem Design. In I3D. 167ś174.

Guillaume Cordonnier, Eric Galin, James Gain, Bedrich Benes, Eric Guérin, Adrien Peytavie, and Marie-Paule Cani. 2017. Authoring landscapes by combining ecosystem and terrain erosion simulation. ACM Trans. Graph. 36, 4 (2017), 134

Franck Courchamp, Ludek Berec, and Joanna Gascoigne. 2008. Allee effects in ecology and conservation. Oxford University Press.

Oliver Deussen, Pat Hanrahan, Bernd Lintermann, Radomir Měch, Matt Pharr, and Przemyslaw Prusinkiewicz. 1998. Realistic Modeling and Rendering of Plant Ecosystems. In Proc. of Sigg. (SIGGRAPH ’98). ACM, 275ś286.

Pierre Ecormier-Nocca, Julien Pettré, Pooran Memari, and Marie-Paule Cani. 2019. Image-based authoring of herd animations. Computer Animation and Virtual Worlds 30, 3-4 (2019).

James Gain, Harry Long, Guillaume Cordonnier, and Marie-Paule Cani. 2017. EcoBrush: Interactive Control of Visually Consistent Large-Scale Ecosystems. Eurographics 36 (2017).

Eric Galin, Eric Guérin, Adrien Peytavie, Guillaume Cordonnier, Marie-Paule Cani, Bedrich Benes, and James Gain. 2019. A Review of Digital Terrain Modeling. Computer Graphics Forum 38, 2 (2019).

Konrad Kapp, James Gain, Eric Guérin, Eric Galin, and Adrien Peytavie. 2020. Data-driven authoring of large-scale ecosystems. ACM TOG 39, 6 (2020), 1-14.

Michel Loreau. 2010. From populations to ecosystems: Theoretical foundations for a new ecological synthesis (MPB-46). Vol. 50. Princeton University Press.

Axel López, François Chaumette, Eric Marchand, and Julien Pettré. 2019. Character navigation in dynamic environments based on optical flow. Computer Graphics Forum 38, 2 (2019).

Darryl I MacKenzie, James D Nichols, J Andrew Royle, Kenneth H Pollock, Larissa Bailey, and James E Hines. 2017. Occupancy estimation and modeling: inferring patterns and dynamics of species occurrence. Elsevier.

Milosz Makowski, Torsten Hädrich, Jan Scheffczyk, Dominic L. Michels, Sören Pirk, and Wojtek Palubicki. 2019. Synthetic Silviculture: Multi-scale Modeling of Plant Ecosystems. ACM Trans. Graph. 38, 4 (2019).

Jan Ondřej, Julien Pettré, Anne-Hélène Olivier, and Stéphane Donikian. 2010. A synthetic-vision based steering approach for crowd simulation. ACM Transactions on Graphics 29, 4 (July 2010), 1.

Sébastien Paris, Julien Pettré, and Stéphane Donikian. 2007. Pedestrian Reactive Navigation for Crowd Simulation: a Predictive Approach. Computer Graphics Forum 26, 3 (Sept. 2007), 665-674. https://doi.org/10.1111/j.1467-8659.2007.01090.x

Craig W. Reynolds. 1987. Flocks, herds and schools: A distributed behavioral model. ACM SIGGRAPH Computer Graphics 21, 4 (Aug. 1987), 25-34.

Craig W Reynolds. 1999. Steering Behaviors For Autonomous Characters. 21.

Stephen R Shifley, Hong S He, Heike Lischke, Wen J Wang, Wenchi Jin, Eric J Gustafson, Jonathan R Thompson, Frank R Thompson, William D Dijak, and Jian Yang. 2017. The past and future of modeling forest dynamics: from growth and yield curves to forest landscape models. Landscape ecology 32, 7 (2017), 1307-1325.

Ruben Smelik, Tim Tutenel, Rafael Bidarra, and Bedrich Benes. 2014. A Survey on Procedural Modelling for Virtual Worlds. Computer Graphics Forum 33, 6 (2014).

Tela-Botanica. DB. https://www.tela-botanica.org/. Accessed: 2020-01-22.

Jur van den Berg, Ming Lin, and Dinesh Manocha. 2008. Reciprocal Velocity Obstacles for real-time multi-agent navigation. IEEE, 1928-1935.

Xinjie Wang, Linling Zhou, Zhigang Deng, and Xiaogang Jin. 2014. Flock morphing animation. Computer Animation and Virtual Worlds 25, 3-4 (May 2014), 351-360.

Jiayi Xu, Xiaogang Jin, Yizhou Yu, Tian Shen, and Mingdong Zhou. 2008. Shape-constrained flock animation. Computer Animation and Virtual Worlds 19, 3-4 (2008).

---

Latex

\textup{fits}\left ( s, R \right ) = \min_{r \in R} \left ( \frac{\min \left ( \mathfrak{F}_{max}\left ( s, R \right ), r_{max} \right ) - \max \left ( \mathfrak{F}_{min}\left ( s, R \right ), r_{min} \right )}{\left (r_{max} - r_{min}\right )} \right )

P_{s}\left ( v \right ) = \sum_{r \in R \left ( s \right ) }{ \left( \frac{q\left ( r, v\right )}{q\left ( r, C\right )} \cdot \frac{c\left ( s, r\right )}{c\left ( s, R\left(s\right)\right )}\right )}

P_{s}\left ( v' \mid v \right ) = \frac{t_{s}^{-1}\left (v, v' \right ) \cdot P_{s}\left ( v' \right )}{\sum_{v''} \left ( t_{s}^{-1}\left (v, v'' \right ) \cdot P_{s}\left ( v'' \right ) \right )}

w_{vv'} = \sum_{s} m_{s} \cdot \left \| s \right \| \left ( P_{s}\left ( v \right ) \cdot P_{s}\left ( v' \mid v \right ) + P_{s}\left ( v' \right ) \cdot P_{s}\left ( v \mid v' \right ) \right )

Planning(h) = \left \{ \left ( v_1, t_1, t_1' \right ), \cdots , \left ( v_n, t_n, t_n' \right ) \right \}