마칭 큐브 공부 노트 (2021.11.12)

Home

명시적 곡면과 암시적 곡면1

우선 명시적 곡면과 암시적 곡면의 차이를 이해해야 한다. 명시적 곡면이란 우리가 OpenGL이나 DirectX에 직접 정점 자료와 색인 자료를 넘겨주듯이 일일이 공간에 이미 정점과 모서리가 주어진 곡면을 의미한다. 암시적 곡면이란 고등학교 기하와 벡터, 혹은 대학교 선형대수나 그래픽스 수업에서 자주 다루었던 F(x, y, z) = 0 형태의 함수를 의미한다. x + 2y - 3z + 1 = 0라는 식이 3차원 평면을 의미함은 그 누구라도 알 수 있다. 이게 우리 눈에는 좀 더 익고 보기 편하더라도, 이걸 결국 정점과 색인 자료로, 즉 명시적으로 표현해서 렌더링을 해줘야한다.

다각형 메시로의 변형2

암시적 곡면을 명시적 곡면으로 변환하는 방법을 이해하려면 말이 아니라 그림으로 이해해야한다. 우선 공간을 격자로 나눈다고 상상해보자. 그러면 격자에 의해 이 공간이 정육면체 그리드로 나뉠 것이다. 각 그리드엔 여덟 개의 꼭짓점이 있을 것이고, 이 꼭짓점을 암시적 곡면의 입력변수로 줄 수 있을 것이다. 그 결과가 만약 0과 같다면, 그 점은 곡면 위의 점이다. 만약 0보다 크다면 곡면 밖의 점이다. 만약 0보다 작다면 곡면 안의 점이다. 즉, 최소한 그리드의 한 꼭짓점의 값이 0보다 작다면, 적어도 한 메시가 이 그리드를 통과한다는 의미이다. 이것이 마칭 큐브의 핵심 개념이다.

525px-MarchingCubes

위의 그림이 그리드 꼭짓점이 가질 수 있는 모든 가능한 경우이다. 하나 하나 논의하도록 하자. 설명의 편의를 위해, 이 그리드의 크기가 1 × 1 × 1이고, 각 꼭짓점은 각각 (0, 0, 0), (1, 0, 0), (1, 1, 0), (0, 1, 0), (0, 0, 1), (1, 0, 1), (1, 1, 1), (0, 1, 1)의 좌표를 갖는다고 가정하자. 여기서 메시란 삼각형 메시를 의미하는 것이다:

  1. 모든 정점이 곡면 밖에 있으므로 그리드 내에 메시가 존재하지 않는다.
  2. 한 정점 (1, 0, 0) 만이 곡면 안에 있으므로 그 정점을 지나는 모든 모서리를 지나는 메시가 하나 생긴다.
  3. 두 인접한 정점이 곡면 안에 있으므로, 이 정점을 지나는 모든 모서리 중 인접한 정점으로 정의된 모서리를 제외한 모서리를 지나는 메시가 생긴다.
  4. 두 인접하지 않은 정점이 곡면 안에 있으므로, 이 정점을 지나는 모든 모서리를 지나는 메시가 생긴다.
  5. 세 인접한 정점이 곡면 안에 있으므로, 이 세 정점 간에 생긴 모서리를 제외한, 이 정점을 하나만 포함하는 모든 모서리를 지나는 메시가 생긴다.
  6. …

기본 개념을 설명하기 위해 우선 정점의 값이 0이 되는 경우를 제외했다. 또한 14번째 그림처럼 메시가 여러 방법으로 존재할 수 있는 그리드에 대해서도 언급하지 않았다.

위의 과정이 종료되면 위상적으로는 유효한 isocurve를 갖게 됨. 이제 각 그리드 모서리의 어디를 메시가 지나야하는지를 정해주면 됨 (지금은 중점이라고 대충 해놨음).

이 isosurface로부터 얻을 수 있는 속성들:

만약 그리드 정점의 값이 0이라면, 일단 0보다는 살짝 큰 값을 줘서 알고리듬을 돌려준 다음(그럼 여러 정점이 생길 것이다), 마지막에 가서 하나의 정점으로 통일해준다.

하나 이상의 그리드 정점의 값이 0이라면, 위와 동일하게 값 약간 바꿔주고 마지막에 복구해준다.

마칭 큐브

  1. 모든 그리드 정점이 0이 아니라고 가정
    • 값이 0이라면 임의의 작은 수를 부여
  2. isosurface를 구하고, 그리드 정점에 따라 올바른 위치로 옮김

그리드의 꼭짓점 여덟 개의 패턴을 8 비트 이진수로 표현해줄 수 있다. 이를 룩업 테이블로 만들어줄 수 있다. 나중에 정점들의 실제 위치는 보간해주면 되니깐.

그리드 모서리는 isocurve 정점이 있을 수도, 하나 있을 수도 있다. 만약 후자의 경우라면, 해당 모서리에 인접한 다른 그리드와 정점을 공유하는 것이다. 하지만, 정점을 공유한다고 해서 서로 마주보는 면이 동일하게 모서리를 갖고 있다는 건 아닐 수도 있다. 서로 일관되지 않으면 그리드 안에 모서리가 존재한다는 모순적인 상황이 발생하므로, 일관성을 맞춰주기 위해 모든 256 가지의 경우에 대응하는 256 가지 모델을 사용해야한다.

렌더링3

마칭 큐브와 같은 알고리듬으로 좀 더 부드러운 메시 곡면을 구하는 방법을 곡면 추출 혹은 다각형화라 부른다. 각 복셀을 박스가 아니라 점이라고 간주하고, 이러한 점 여덟 개를 2 × 2 × 2 그리드의 꼭짓점이라고 간주하는 것이다.

암시적에서 매개변수적으로4

등곡면 추출이란 암시적 혹은 부피적 표현을 삼각형 메시로 변환하는 과정을 의미한다. 사실상 이 방법의 대표 주자는 마칭 큐브 알고리듬이다.

등곡면 S가 지나가는 각 셀마다 지역적인 요소에 따라 곡면의 일부분이 생성이 됨. 이걸 전부 모으면 완전한 등곡면 S의 대략적인 근사가 나올 것이다.

곡면 S와 교차하는 모든 그리드 모서리마다 마칭 큐브 알고리듬에 의해 이 교차를 근사하는 점을 구한다. 스칼라장 F로 말하자면, F의 부호는 그리드 모서리의 끝점 p1과 p2에 의해 결정된다. F의 삼중선형 근사가 사실상 그리드 모서리에 대해서는 선형이기에 교차점 s는 모서리의 끝점의 거리값 d1 := F(p1)과 d2 := F(p2) 간의 선형 보간으로 구할 수 있다:

s = (|d2| / (|d1| + |d2|)) p1 + (|d1| / (|d1| + |d2|)) p2

각 셀에서 결과적으로 구한 점을 이어 삼각형으로 된 전체 곡면의 부분을 구할 수 있으며, 이는 모서리 교차하는 모든 경우의 수에 대응하는 룩업 테이블에 따라 적용된다. 모든 가능한 경우의 수는 셀의 모서리의 부호와 숫자에 의해 결정되므로, 테이블의 크기는 28 = 256이다.

가끔 추출된 곡면에 애매모호한 부분 때문에 크레바스 마냥 쪼개진 부분이 있곤 하다. 이런 건 물론 제대로 룩업 테이블을 수정하면 간단하면서 효율적으로 구할 수 있으나, F의 부호 역전에 대한 대칭성을 포기하게 된다 [Montani et al. 94]5. 결과적으로 얻는 등곡면은 빈틈 없는 2차 다양체를 얻을 수 있으며, 이는 메시 복구 기법에 이용할 수 있다.

마칭 큐브는 오로지 정규화된 그리드의 모서리에 대한 교차점만 구하므로, 뾰족한 부분들을 제대로 표현하려면 셀 내에 추가적인 점들을 찍어줘야 한다. 이에 나온 확장 마칭 큐브 알고리듬 [Kobbelt et al. 01]6은 거리 함수의 도함수 ∇F를 바탕으로 셀 내에 뾰족한 특징이 존재하는지 확인하고, 복셀의 모서리와의 교차점에 대한 추정 접면을 교차시켜 추가적인 점들을 찍어 준다.

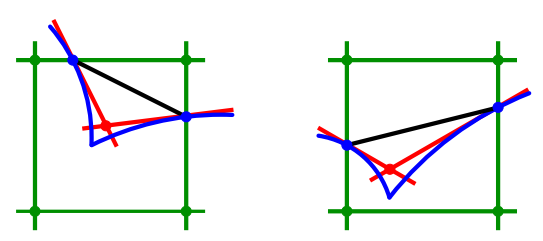
ExtendedMarchingCubes2d

ExtendedMarchingCubes3d

확장 마칭 큐브를 OpenMesh 자료 구조 [Botsch et al. 02]7를 기반으로 구현해놓은 예제는 [Kobbelt et al. 05]8에서 다운 받을 수 있다.

윤곽 대비9

0차 등고선에 대한 메시를 재구축하는 것은 레벨 셋의 흔한 연산 중 하나다. 이에 대한 일반적인 방법으로는 마칭 큐브 알고리듬이 있다. Wyvill et al.10이 발명했으며, 이후 Lorensen과 Cline11에 의해 독립적으로 발명되었다. 핵심 아이디어는 0차 등곡면이 3차원 그리드의 모서리를 지나는 곳에 메시 정점을 생성하고, 이 정점들을 그리드 셀 내에서 연결해주어 0차 등곡면을 근사해주는 것이다.

그리드 셀의 꼭짓점에 저장된 값 간의 레벨 셋 함수의 선형 보간이라는 가정 하에 0차 등곡면이 그리드 모서리의 어디를 지나는지는 쉽다. 예를 들어 (i, j, k)와 (i + 1, j, k) 사이의 모서리에 0차 교차가 있는 것은 Φi, j, k의 부호가 Φi + 1, j, k의 부호의 정반대임과 필요충분 조건이며, 이 두 점 간의 선형 보간의 0은 다음 분수에서 발생한다:

θ = Φi, j, k / (Φi, j, k - Φi - 1, j, k)

즉, 좌표 ((i + θ)Δx, jΔx, kΔx)에서 발생한다.

만약 그리드의 하나 이상의 레벨 셋 값이 정확히 0, 즉 Φi, j, k = 0이라면, 모든 면이 닫혀있는 메시를 생성해주는 강력한 알고리듬을 만들기가 어려워진다. 가장 간단한 해법은 이 0들을 단일 정밀도 소수 기준 10-36과 같은 매우 작은 값을 주는 것이다. 이 정도로 작은 값을 가질 경우 반올림 오류에 의해, 메시 정점의 위치에는 영향을 주지 않을 것이지만 메시 생성 코드에 예외 처리를 해줄 필요가 없다는 매우 큰 장점을 갖는다.

0차 등곡면을 갖는 그리드 셀, 즉 꼭짓점의 Φ 간 부호가 다른 경우, 메시 정점 간에 적절한 모서리를 찾아 연결해주는 것은 간단한 일은 아니다. 고려해야할 경우가 총 254 가지이며, 룩업 테이블로 복잡도를 해결하더라도 Lorensen과 Cline의 초기 방법은 위상적 모호함12에 의해 구멍이 송송 뚫려있는 경우가 있곤 했다. 이에 대한 해결 방법 중 하나가 마칭 사면체13이다. 이 방법에선 우선 각 그리드 셀을 더 작은 사면체 (공유 그리드 면에 정렬하여 모든공간에서 유효한 사면체 메시를 형성함)로 분해한 후, 사면체의 모서리에 대한 0차 교차 정점을 생성하고 이들을 연결하여 사면체 간 독립적으로 메시 면을 형성해준다.

마칭으로 형성한 삼각형 메시들은 보통 품질이 그리 좋은 편은 아니다. 만약 등곡면이 겨우 그리드 점 하나를 포함하고 있다면, 근처에 생성되는 삼각형이 사실상 하나 이상의 짧은 모서리로 이루어진 조각처럼 되곤 한다. 대부분의 경우 메시 스무딩이 필요하기도 하다: 각 정점을 이웃 정점의 평균으로 옮겨주고 레벨 셋을 통해 0차 등곡면으로 사영해준다. 이러면 더 보기 좋은 균일한 크기의 삼각형을 만들어주면서도 레벨 셋에 잘 따르게 된다.

마칭 큐브 등곡면14

알고리듬:

  1. main(argc, argv)
  2. runGraphicsTest(argc, argv)
    1. initGL(argc, argv)
    2. findCudaDevice(argc, argv)
    3. GLUT에 콜백 함수 등록
    4. initMC(argc, argv)
      1. 그리드 크기 설정 (25, 25, 25), 0001 0000
      2. 그리드 크기 마스크 설정 (25 - 1, 25 - 1, 25 - 1), 0000 1111
      3. 그리드 크기 시프트 설정 (0, 5, 10)
      4. 복셀 개수 설정 = 25 * 25 * 25 = 32,768
      5. 복셀 크기 설정 = (2.0f / gridSize)
      6. 최대 정점 개수 설정 = gridSize.x * gridSize.y * 100
      7. 샘플 볼륨 데이터 불러온 뒤 GPU 메모리에 복사
      8. CUDA에서 볼륨 텍스처 생성
      9. 위치와 법선용 VBO 생성
      10. allocateTextures(deviceEdgeTable, deviceTriTable, deviceNumVertsTable)
      11. GPU 메모리 할당
        1. 복셀 정점
        2. 복셀 정점 스캔
        3. 복셀 차지 중인 정점
        4. 복셀 차지 중인 정점 스캔
        5. 압축 복셀 배열
  3. display()
    1. computeIsosurface()
      1. 복셀 당 필요한 정점 개수 연산 launch_classifyVoxel(grid, threads, voxelVertices, voxelOccupied, volume, gridSize, gridSizeShift, gridSizeMask, numVoxels, voxelSize, isoValue)
        1. 복셀 당 필요한 정점 개수 연산 classifyVoxel(voxelVertices, voxelOccupied, volume, gridSize, gridSizeShift, gridSizeMask, numVoxels, voxelSize, isoValue, numVerticesTextureObject, volumeTextureObject)
        2. 복셀 차지 중 정점 배열 스캔 ThrustScanWrapper(output, input, numElements)
        3. 값 읽어서 비어있지 않은 정점 총 개수 계산. 배타적 스캔을 사용하므로 총 값은 스캔 결과의 마지막 값에 입력 배열의 마지막 값을 더한 값.
        4. 활성화/가득 찬 복셀이 없으면 반환
        5. 복셀 색인 배열 압축 launch_compactVoxels(grid, threads, compactedVoxelArray, voxelOccupied, voxelOccupiedScan, numVoxels)
        6. 복셀 정점 개수 배열 스캔 ThrustScanWrapper(output, input, numElements)
        7. 정점 총 개수 읽어오기
        8. 삼각형 생성 후 정점 버퍼에 쓰기
        9. 빈 복셀 생략
        10. launch_generateTriangles2(grid, threads, pos, norm, compactedVoxelArray, numVertsScanned, volume, gridSize, gridSizeShift, gridSizeMask, voxelSize, isoValue, activeVoxels, maxVerts)
    2. GL로 시각화
      1. 뷰 행렬 설정
      2. 라이팅
      3. renderIsosurface()

1. 이 문단은 김도엽 저자의 <The Fluid Engine Development>를 참고하여 작성함

2. 이 문단은 James D. Foley, Andries van Dam, Steven K. Feiner, John Hughes, Morgan McGuire, David F. Sklar, Kurt Akeley 저자의 <Computer Graphics Principles Practice>을 참고하여 작성함

3. 이 문단은 Tomas Akenine-Möller, Eric Haines, Naty Hoffman, Angelo Pesce, Michał Iwanicki, Sébastien Hillaire 저자의 <Real-Time Rendering>을 참고하여 작성함

4. 이 문단은 Leif Kobbelt, Mario Botsch, Mark Pauly 저자의 <Polygon Mesh Processing>을 참고하여 작성함

5. C. Montani, R. Scateni, and R. Scopigno. “A Modified Look-up Table for Implicit Disambiguation of Marching Cubes.” The Visual Computer 10:6 (1994), 353–55.

6. L. Kobbelt, M. Botsch, U. Schwanecke, and H.-P. Seidel. “Feature Sensitive Surface Extraction from Volume Data.” In Proc. of ACM SIGGRAPH, pp. 57–66. New York: ACM, 2001.

7. M. Botsch, S. Steinberg, S. Bischoff, and L. Kobbelt. “OpenMesh – a generic and efficient polygon mesh data structure.” Presented at the OpenSG Symposium 02, 2002

8. L. Kobbelt, M. Botsch, U. Schwanecke, and H.-P. Seidel. “Extended Marching Cubes Implementation.” , 2002–2005.

9. 이 문단은 Robert Bridson 저자의 <Fluid Simulation>을 참고하여 작성함

10. Geoff Wyvill, Craig McPheeters, and Brian Wyvill. Data Structure for Soft Objects. The Visual Computer, 2(4):227–234, February 1986.

11. William E. Lorensen and Harvey E. Cline. Marching cubes: A high resolution 3d surface construction algorithm. In Proc. ACM SIGGRAPH, pages 163–169, 1987.

12. Martin J. Dürst. 1988. Re: additional reference to "marching cubes". SIGGRAPH Comput. Graph. 22, 5 (Oct. 1988), 243.

13. Heinrich Müller and Michael Wehle. Visualization of implicit surfaces using adaptive tetrahedrizations. In Dagstuhl ’97, Scientific Visualization, pages 243–250, 1999.

14. 마칭 큐브 NVIDA CUDA 샘플: 링크