ReSTIR 논문 정리 (2022.10.16)

Benedikt Bitterli, Dartmouth College
Chris Wyman, NVIDIA
Matt Pharr, NVIDIA
Peter Shirley, NVIDIA
Aaron Lefohn, NVIDIA
Wojciech Jarosz, Dartmouth College

초록

문제: 수백만 개의 동적인 광원으로부터의 직접광을 몬테 카를로 적분법을 활용하여 효율적으로 렌더링하기
해결: ReSTIR 알고리듬

interactive rate
고퀄리티
복잡한 자료구조 X

후보 빛 샘플 집합으로부터 다시 표집, 즉 재표집resample을 반복적으로 수행하고, 추가적으로 시공간적 재표집을 통해 근처 샘플들로부터 추가적인 정보를 활용해줌.

위의 방법을 활용하는 무편향 몬테 카를로 추정량을 제시함. GPU에서 돌아가도록 구현하였으며, 340만 개의 동적인 광원 삼각형들이 있는 복잡한 장면을 픽셀 당 최대 8 개의 광선을 활용하여 렌더링하는데에 프레임 당 50ms 이하의 성능을 보임.

1. 도입

몬테 카를로 경로 추적법이 요즘 오프라인 렌더링에 널리 사용 중이고, 실시간에서도 RTX의 등장 덕에 슬슬 사용하려고 함. 어차피 오프라인 렌더링할 때도 광원이 많을 때 직접광 처리하는 법은 매우 어려움.

근데 여기다가 실시간을 보장하겠다? 그럼 장면이 동적일테니 렌더러는 사전에 장면이 어떻게 변할지 모를 것임. 게다가 현재로서는 실시간성을 보정하면서 광선을 쏘기엔 픽셀당 겨우 몇 개 밖에 못 쏨.

그러니까 사람들이 디노이징 기술을 연구하기 시작하고, 상당한 결과를 보였음. 근데 애초에 처음부터 디노이저에 표본이 적은 이미지, 즉 노이즈가 심한 이미지를 주면 디노이저도 제대로 처리하기가 힘듦. 즉, 샘플링을 첨부터 잘 해야 디노이저도 잘 될 것이라는 뜻임.

우리가 제시한 방법은 완전히 동적이고, 여러 광원을 갖는 장면에서 단일 튕김 직접광을 표집하는 실시간 광선 추적법임. 이 방법은 우선 재표집된 중요도 표집(RIS)에 기반함. 여기에다가 원하는 표본들만 저장할 “저장소”라는 고정된 자료구조와 이에 대한 알고리듬을 활용하여 안정적인 실시간 성능을 보장함.

여기서 저장소라는 것은 고정된 크기의 배열을 의미함. 이때 이 저장소를 활용할 때 시공간적 이웃들의 저장소 통계를 재사용해서 확률적으로, 점진적으로, 계층적으로 픽셀의 직접광 표집 PDF를 개선함. 요즘 실시간 디노이저들이 시공간 이웃들의 픽셀 색pixel color을 재사용하는 것에 반해 이 논문에서 말하는 재사용이란 렌더러 내부에서 사용하는 표집 확률sampling probabilities을 의미함. 그렇기에 무편향한 것임.

2. 이론적 배경

어떤 점 y에서 직접광에 의해 방향 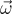DirectionOmega 로 반사된 radiance L은 모든 광원 표면 A에 대한 적분으로 구할 수 있음:

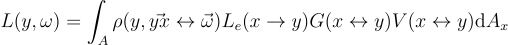
ReflectedRadianceL

ρ: BSDF
L_e: 광원 radiance
V: x와 y 사이의 상호 가시성
G: 기하항. 역제곱 거리와 코사인항

보는 방향 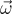DirectionOmega 와 shading할 점 y를 편의성을 위해 빼놓고 넓이의 변화량을 dx로 표기하면 다음과 같이 L을 간단하게 표현할 수 있음:

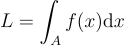
SimplifiedReflectedRadianceL

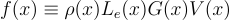
IntegrandF

여기에 중요도 표집Importance Sampling(IS)를 적용하면 다음과 같아짐:

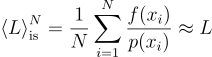
ImportanceSampling

여기에 다중 중요도 표집Multiple Importance Sampling(MIS)를 적용할 경우 다음과 같아짐:

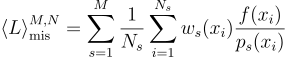
MultipleImportanceSampling

여기서 w_s 함수는 가중치 함수로, 주로 균형 휴리스틱 함수 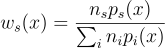BalanceHeuristic 사용함.

2.1. RIS

MIS 대신 사용할 수 있는 방법에는 몇몇 항의 곱에 근사하게 비례하는 표본을 뽑는 방법이 있음. 즉, RIS를 사용하는 것임.

예를 들어, 우리가 구해야하는 target PDF 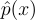TargetPdf 에서 표집을 하려고 보니, 실질적으로 그게 불가능하다면, 이 PDF에 근사할 수 있도록 source PDF p를 구하는 것임.

즉, 적당히 최적인 PDF p에서 z 개의 표본을 우선 뽑아보고, 이 집합에서 확률 p(z | x)에 따라 한 표본을 또다시 뽑는 것임. 이때의 표본 집합의 모든 z 개의 표본은 각각 가중치를 갖는데, 이 가중치에 비례하여 확률을 부여함. 이때 한 표본을 뽑을 때, target PDF에 근사하게 표본을 뽑아야 하므로 가중치에 target PDF의 정보를 추가함:

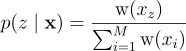
ResampledImportanceSamplingCandidateProbability

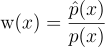
ResampledImportanceSamplingCandidateWeight

이런 방법을 사용하여 최종적으로 샘플 y ≡ x_z를 뽑게 됨.

이때 단일 표본 RIS 추정량은 다음과 같음:

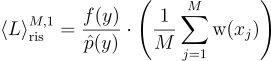
SingleSampleRisEstimator

즉, 추정량은 마치 y가 p가 아니라 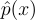TargetPdf 에서 온 것으로 착각하게 되고, 괄호 안의 항을 통해 실제로는 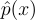를 근사하고 있음을 알 수 있음.

RIS를 여러 표본에 대해 반복하고 평균을 내게 되면 N개 표본 RIS 추정량을 얻을 수 있음:

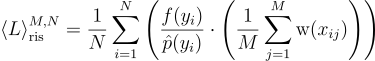
NSampleRisEstimator

이 논문에서는 단일 표본을 가정하고 진행함.

일반적으로 각 픽셀 q는 고유한 피적분함수 f_q와 이에 대응하는 target PDF TargetPdfForPixelQ 를 가질 것임.

RIS 알고리듬은 다음과 같음:

알고리듬 1: RIS

입력: M, q: 픽셀 q에 대해 생성할 후보 표본의 수 M(M ≥ 1)
출력: 표본 y와 RIS 가중치의 합 SumOfRisWeights

// 후보군 x = {x_1, ..., x_M} 생성
x ← 0
w ← 0
w_sum ← 0
for i ← 1 to M do
    generate x[i] ~ p
    x ← x ∪ {x[i]}
    w[i] ← phat_q(x[i]) / p(x[i])
    w_sum ← w_sum + w[i]
    w ← w ∪ {w[i]}
// 후보군 x에서 y 선택
w로부터 정규화된 CDF C 계산
C를 활용하여 w_z에 비례하여 무작위로 인덱스 z ∈ [0, M) 뽑기
y ← x[z]
return y, w_sum

RIS와 MIS 섞기

위에서는 source PDF p가 하나라고 가정했지만, MIS에서 그랬듯, 여러 이미 잘 되는 표집 기술들이 존재함. 어차피 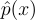TargetPdf 가 양수일 때 p가 양수이기만 하면 M → ∞일 수록 y의 분포는 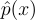에 점근하지만, source PDF p의 생김새는 y의 PDF가 얼마나 잘 되느냐와 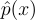에 얼마나 빠르게 수렴하느냐를 결정하기도 함. 실제로 target PDF 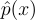가 두 함수의 곱(예를 들면 lighting × BSDF)이라고 하면, y의 PDF가 얼마나 잘 되느냐는 source PDF가 어떤 함수(lighting? 아니면 BSDF?)에서 왔느냐에 따라 다름.

다행히도 RIS 내부적으로 MIS를 사용하여 분산 줄이기를 해줄 수 있음. MIS를 통해 후보군 명단을 뽑은 다음, 여기서 구한 MIS(혼합) PDF를 source PDF로 사용하여 남은 RIS를 처리해주면 됨.

근데 MIS의 복잡도는 사용하는 기술의 개수에 따라 제곱에 비례하여 증가함.

여기서는 후보의 개수를 늘리는 방법으로 시공간 재사용을 해줌. 이때 시간적으로나 공간적으로나 각각 다른 source PDF와 피적분함수 영역을 사용함.

2.2. 가중치 저장소 표집

가중치 저장소 표집Weighted reservoir sampling (WRS)이란 어떤 연속된, 지속적으로 들어오는 데이터 스트림stream {x₁, … x_M}에 대해서 N 개의 원소를 무작위로 표집하는 알고리듬의 한 종류임. RIS에서처럼 각 원소에는 가중치 w(x_i)가 있으며, 이 가중치에 따른 확률로 x_i를 선택하게 됨:

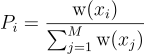
WrsWeightsProbability

저장소 표집은 원소마다 딱 한 번만 처리하며, 메모리엔 오로지 N 개의 원소만 있을 수 있다. 스트림의 크기 M은 사전에 몰라도 됨.

보통 저장소 표집 알고리듬은 원소 x_i가 출력 집합에 여러 번 등장할 수 있는지 여부로 분류하곤 함. 즉, 표본을 고를 때, 대체할 표본이 있냐 없냐를 보는 것. 몬테 카를로의 경우 x_i를 독립적으로 고를 것이기 때문에 대체할 표본이 있는 WRS를 다룰 것임.

저장소 표집은 입력 스트림의 원소를 들어온 순서대로 처리하며, N 개의 표본을 저장할 수 있는 저장소reservoir에 표본을 저장함. 스트림의 어느 시점에서나 저장소 표집은, 저장소의 표본들이 목표하는 분포(현재까지 처리한 모든 원소에 대해서)로부터 뽑히도록하는 불변량을 유지함. 스트림이 끝나면 저장소를 반환함. 이 논문에서는 N = 1, 즉 저장소에 표본이 딱 하나 밖에 없는 경우만 다룸.

스트림에 새 원소가 들어오면, 불변량을 유지하기 위해 저장소를 갱신해줘야 함. 즉, m 개의 표본을 처리한 이후에 표본 x_i가 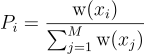WrsWeightsProbability 의 확률로 저장소에 등장한다는 것. 갱신 규칙에 의해 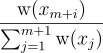ReservoirReplacementProbability 의 확률로 저장소에 있는 x_i를 다음 표본 x_{m + 1}으로 교체한다. 이를 통해 x_{m + 1}가 원하는 빈도에 따라 저장소에 등장할 수 있도록 해줌. 즉, 임의의 이전 표본 x_i가 저장소에 있을 확률은 다음과 같음:

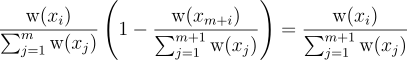
XiRemainingInReservoirProbability

이를 통해 불변량이 유지됨.

알고리듬 2: WRS

class Reservoir
    y ← 0       // 출력 표본
    w_sum ← 0   // 가중치합
    M ← 0       // 지금까지 처리한 표본의 수
    function update(x_i, w_i)
        w_sum ← w_sum + w_i
        M ← M + 1
        if rand() < (w_i / w_sum) then
            y ← x_i
function reservoirSampling(S)
    Reservoir r
    for i ← 1 to M do
        r.update(S[i], weight(S[i]))
    return r

3. 시공간 재사용과 함께 RIS 스트리밍하기

RIS와 WRS가 ReSTIR 알고리듬의 기본임. 이 둘을 바탕으로 알고리듬과 자료구조를 간단하게 유지하면서도 스트리밍을 통해 무작위로 후보를 처리할 수 있게 해줌. 이를 통해 WRS의 속성에 의해 시공간 재표집spatiotemporal resampling을 통해 이웃 픽셀과 이전 프레임의 후보를 효율적으로 재사용하고 합칠 수 있는 방법을 소개함.

다만, 너무 순진하게 이웃 픽셀의 표본들이 서로 다른 BRDF에서 왔다는 점과 표면의 orientation이 서로 다르다는 점을 고려 안 하고 시공간 재표집을 하게되면 편향성이 생길 것임. 이러면 기하적으로 불연속적인 구간에서 에너지 손실이 발생하게 됨.

3.1. 저장소 표집으로 RIS 스트리밍하기

WRS 알고리듬을 RIS에 적용해서 스트리밍 알고리듬으로 바꾸는 건 쉬움. 그냥 저장소를 연속적으로 생성된 후보 x_i와 이에 대응하는 가중치에 따라 갱신해주면 됨.

알고리듬 3: WRS를 활용한 RIS 스트리밍

foreach 픽셀 q ∈ Image do
    Image[q] ← shadePixel(RIS(q), q)
function RIS(q)
    Reservoir r
    for i ← 1 to M do
        generate x_i ~ p
        r.update(x_i, phat_q(x_i) / p(x_i))
    r.W = (1 / (phat_q(r.y))) * ((1 / r.M) * r.w_sum) // 단일 표본 RIS 추정량
    return r
function shadePixel(Reservoir r, q)
    return f_q(r.y) * r.W

우선 광원의 표면에서 균등하게 표본을 생성한 다음, 그림자가 져있지 않은 경로의 contribution TargetDistribution 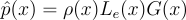를 target 분포로 삼아 살아남은 N 개의 RIS 표본에 대해서 그림자 광선만을 추적해줌. M의 개수에 따라 얼마나 잘 렌더링이 되는지를 확인해본 결과, M이 증가할 수록 RIS가 제일 렌더링이 잘 됨. 위의 알고리듬은 공간 복잡도 자체는 상수지만, 시간 복잡도 자체는 O(M)임.

3.2. 시공간 재사용

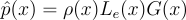위에서 언급한 방법은 각 픽셀 q에서 독립적으로 후보를 생성하고, 이를 target PDF TargetPdfForPixelQ 에 따라 재표집을 해준 것임. 참고로, 이웃의 픽셀 간에는 상당한 상관관계가 존재함. 예를 들어 그림자가 지지 않은 조명( TargetDistribution )을 사용할 경우, 공간적으로 보면 당연히 근처 픽셀들의 geometry 항이나 BSDF 항은 비슷하지 않겠음? 이 상관관계를 처리하는 가장 순진한 방법은 픽셀마다 후보군과 가중치를 생성하고, 두번째 단계에서 자기 픽셀과 이웃의 픽셀을 합쳐서 재사용reuse을 해주는 것임. 가중치 연산은 첫번째 단계에서 처리가 될테니까 이웃 후보군을 재사용하는게 같은 수의 후보군을 새롭게 생성하는 것보다 더 효율적임.

근데 이건 실제로 불가능함. 재사용할 후보마다 저장을 해야되니까. 이걸 피할 수 있는 방법으로는 저장소 표집의 중요한 속성을 활용하면 됨. 즉, 입력 스트림에 접근할 필요도 없이 여러 저장소를 합칠 수 있다는 점임.

저장소는 보통 현재 선택한 표본 y와 현재까지 처리한 표본들의 가중치의 합 w_sum이라는 상태를 가짐. 두 저장소를 합치려면 각 저장소의 y를 마치 w_sum의 가중치를 갖는 새 표본으로 간주하고 이걸 새 저장소의 입력으로 넣어주면 됨. 수학적으로 보면 두 저장소의 입력 스트림을 합쳐서 저장소 표집을 해준 거랑 똑같음. 시간 복잡도도 상수인데다가, 그 어느 스트림에도 후보를 저장해줄 필요도 없음. 그냥 처리할 저장소의 현재 상태만 갖다 쓰면 됨.

알고리듬 4: 여러 저장소 스트림 합치기

입력: 합칠 저장소 r_i
출력: r₁, …, r_k의 입력 스트림을 이어 붙인 것과 같은 합쳐진 저장소
1   function combineReservoirs(q, r_1, r_2, ..., r_k)
2       Reservoir s
3       foreach r ∈ {r_1, ..., r_k} do
4           s.update(r.y, phat_q(r.y) * r.W * r.M)
5       s.M ← r_1.M + r_2.M + ... + r_k.M
6       s.W = (1 / (phat_q(s.y))) * ((1 / (s.M)) * s.w_sum) // 단일 표본 RIS 추정량
7       return s

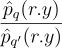보면 알겠지만 O(k)의 시간 복잡도를 가짐. 이웃 픽셀 q’의 표본이 서로 다른 target 분포 NeighboringPixelTargetPdf 를 갖고 있다는 점을 잊으면 안 됨. 그러므로 표본을 NeighboringTargetPdfFactor 로 다시 작성해주어 현재 픽셀에 비해 이웃 쪽이 over/undersample 되었는지 여부를 처리해주어야 함. 결론적으로 얻게 된 식은 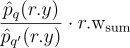ResultingTerm 인데, 알고리듬 3에서의 이미 구한 값으로 치환해주면 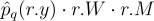ResultTermSuccinct 로 표현해줄 수 있음.

공간 재표집Spatial Reuse

우선 알고리듬 3의 RIS(q) 함수를 통해 모든 픽셀 q마다 M 개의 후보를 생성해주어 프레임 버퍼에 각 저장소를 저장해줌. 두번째 단계로는 각 픽셀이 k 개의 이웃 픽셀을 선택하고, 이웃 픽셀들의 저장소와 자기 저장소를 알고리듬 4를 이용해서 합쳐줌. 각 픽셀마다 시간 복잡도는 O(k + M)이지만, 결국 k · M 개의 후보를 얻게 됨. 게다가 이전 재사용 단계의 결과를 입력으로 활용해서 공간 재사용을 반복해줄 수도 있음. 즉, n 번 반복을 하게되면 O(nk + M)의 복잡도를 갖겠지만, 픽셀 당 kⁿM 개의 후보를 얻을 수 있음.

시간 재표집Temporal Reuse

실시간이면 당연히 프레임이 존재할 것. 그럼 직전 프레임에서 후보를 뽑아서 재사용해줄 수도 있음. 프레임을 렌더링한 다음에 각 픽셀의 최종 저장소를 다음 프레임에서 재사용할 수 있게 저장해두고, 이제 렌더링할 다음 프레임에서는 단순히 직전 프레임 뿐만 아니라 지금까지 렌더링한 모든 직전 프레임의 저장소에서의 후보를 뽑아서 쓸 수 있어 이미지 퀄리티가 훨씬 좋아짐.

가시성 재사용Visibility Reuse

솔직히 후보의 개수는 무한대로 늘어날 순 있지만, 그럼에도 아예 노이즈가 없을 순 없음. M이 무한대로 가면서 표본의 분포가 target PDF 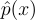TargetPdf 에 점근은 하겠지만, 애초에 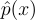자체가 피적분함수 f를 완벽하게 표집하는게 아님. 실무에선 보통 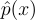를 그림자가 지지 않은 경로의 contribution으로 설정되기 때문에 M이 커질 수록 가시성에 의해 발생하는 노이즈가 생기게 됨. 특히 큰 장면에서는 더욱 그럴 것임. 이걸 해결하기 위해선 가시성 재사용을 진행함. 시공간 재사용하기 전에 우선 각 픽셀의 저장소의 표본 y의 가시성을 확인함. 만약 y가 가려져 있다면 해당 저장소는 버림. 즉, 가려져 있는 표본들은 이웃을 확인하지 않음. 만약 지역적으로 가시성이 일관된 상태라면, 공간 재사용을 한 최종 표본은 가려지지 않은 상태일 것임.

다음은 완성된 알고리듬의 의사 코드임:

알고리듬 5: 시공간 재사용을 적용한 RIS 알고리듬

입력: 직전 프레임의 저장소를 갖는 이미지 크기 버퍼
출력: 현재 프레임의 저장소

function reservoirReuse(prevFrameReservoirs)
  reservoirs ← new Array[ImageSize]
  // 초기 후보군 생성
  foreach 픽셀 q ∈ Image do
    reservoirs[q] ← RIS(q)  // 알고리듬 3
  // 초기 후보들의 가시성 확인
  foreach 픽셀 q ∈ Image do
    if shadowed(reservoirs[q].y) then
      reservoirs[q].W ← 0
  // 시간 재사용
  foreach 픽셀 q ∈ Image do
    q' ← pickTemporalNeighbor(q)
  reservoirs[q] ← combineReservoirs(q, reservoirs[q], prevFrameReservoirs[q'])  // 알고리듬 4
  // 공간 재사용
  for iteration i ← 1 to n do
    foreach 픽셀 q ∈ Image do
      Q ← pickSpatialNeighbors(q)
      R ← {reservoirs[q'] | q' ∈ Q}
      reservoirs[q] ← combineReservoirs(q.reservoirs[q], R)
  // 픽셀 색 연산
  foreach 픽셀 q ∈ Image do
    Image[q] ← shadePixel(reservoirs[q], q) // 알고리듬 3
  return reservoirs

위의 알고리듬에서 보면 알겠지만, 우선 픽셀마다 M 개의 독립적인 light 후보를 생성하고, 재표집을 함. 이 단계에서 재표집한 표본들에 대해 가시성을 확인하고, 가려져 있는 표본들은 거르게 됨. 이렇게 한 번 더 거르고 남은 표본들은 직전 프레임의 출력과 함께 픽셀의 저장소에 합쳐 넣게 됨. 픽셀의 이웃들로부터 정보를 가져와 사용하기 위해 n 번의 공간 재사용을 수행함. 마지막으로 이미지를 쉐이딩 해주고, 최종 저장소를 다음 프레임으로 넘겨줌.

4. 다중 분포 RIS의 편향성 (없애기)

위에 알고리듬에서 다루지 않은 한 가지 중요한 점이 있음: 각 픽셀이 서로 다른 적분 영역과 target 분포를 갖으므로 이웃 픽셀에 의해 편향성이 발생할 수 있음. 왜냐면 서로 target 분포가 다르니까 재표집한 이후의 표본들의 PDF는 픽셀마다 다르기 때문임. 원래 RIS가 서로 다른 PDF에서 온 후보 표본들을 섞는 용도로 만들어진게 아님. 이거 무시하고 그냥 쓰면 노이즈랑 편향성 생김.

4.1. RIS 가중치 분석하기

RIS에서 어느 부분에서 편향성이 발생하는지를 보기 위해 우선 단일 표본 RIS 추정량 공식을 다시 살펴보기로 함:

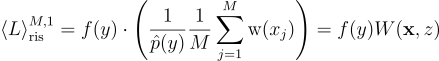
SingleSampleRisEstimatorRegrouped

이때 W는 생성된 표본 y ≡ x_z에 대한 확률 가중치임:

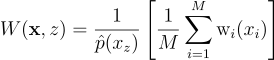
StochasticWeight

이때 W의 역할은 도대체 뭘까?

보통 몬테 카를로 추정량은 f(y) / p(y)의 형태를 띠는데, 이때 우린 p(y)가 뭔지 모름. 근데 위에 식을 보니까 p(y)의 역할이 W(x, z) 안으로 흡수가 되었으니, 어쨋든 W가 PDF의 역수 1/p(y)의 역할을 수행할 것이라고 추측할 것임. 근데 W(x, z)는 보면 확률 변수임. 어떤 출력 표본 y가 주어졌을 때, 이게 어느 {x, z}에서 나왔는지는 모르잖음. 애초에 한 {x, z}에서만 나올 수 있는게 아닐 수도 있으니 답이 여러 개일 수도 있고. 그러니 어떤 값의 집합(즉, W(x, z)의 값)이 RIS에서 반환되는지도 랜덤임.

즉, 단일 표본 RIS 추정량이 무편향성을 띠려면 W(x, z)의 기대값이 1/p(y)과 같아야 함. 나중에 보겠지만, 이웃 픽셀 표본이랑 쓰까는 부분 때문에 W(x, z)의 기대값이 1 / p(y)이 안 될 수도 있어서 편향성이 발생함.

재가중치항 설명

알고리듬 4에 의하면 이웃 표본들의 가중치는 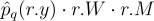ResultTermSuccinct 임. 이걸 위에서는 직관적으로 이해했는데, 이제 좀 더 제대로 이해해보자:

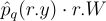StandardRisWeight 는 결국 간단히 말하면 TargetPdfOfPixelQOverSourcePdfP 의 표준 RIS 가중치임. 여기서 문제는 PDF p(r.y)가 뭔지는 모르고, 이 대신 PDF 역수의 추정량 r.W을 사용한다는 것임. r.y가 여러 표본을 합친 결과를 의미하므로, r.y를 생성한 후보들의 수 r.M에 따라 가중치가 추가적으로 scaling됨.

4.2. 편향 RIS

이제 RIS에 의해 생성된 표본들의 PDF p(y)를 구해보자. 표준 RIS에서는 모든 후보 표본이 같은 PDF p에서 올 것이라고 가정하지만, 여기서는 x의 표본 x_i가 서로 다른 source PDF p_i(x_i)에서 왔을 수도 있다고 가정. 이 모든 후보들의 joint PDF는 단순히 모든 PDF를 곱한 것임:

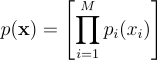
JointPdf

RIS 알고리듬의 2단계에서는 한 인덱스 z ∈ {1, …, M}를 뽑지만, 이때 뽑는 확률과 가중치는 이제 후보의 출신 PDF에 따라 처리함:

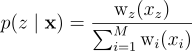
RisCandidateSpecificProbability

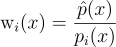
RisCandidateSpecificWeight

p(x)랑 p(z

x)에 대한 식은 있으니 후보군 x와 선택된 인덱스 z에 대한 joint PDF를 다음과 같이 곱으로 나타낼 수 있음:

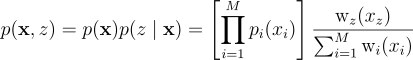
JointPdfRewritten

그래서 p(y)이 무엇이느냐?

고정된 출력 표본 y에 대해서 여러 x, z가 존재할 수 있음. 예를 들어 x₁ = y이고 z = 1이라고 하면 나머지 x₂, …, x_M는 아무거나일 수도 있음. z = 2인 경우도 마찬가지임. 당연히 y는 p_i(y) > 0인 경우에서만 생성되므로, 다음과 같이 집합으로 표현해보자:

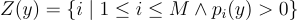
SetOfYs

출력 표본 y에 대한 전체 PDF를 구하려면, 단순히 y를 생성할 수 있는 모든 경우의 수에 대한 joint PDF를 주변부로 처리해주면 됨:

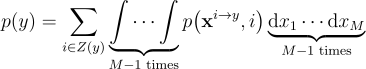
TotalPdfOfAnOutputSampleY

이때 x^{i → y} = {x₁, …, x_{i - 1}, y, x_{i + 1}, …, x_M}을 의미함. 즉, i번째 후보를 y로 픽스한 것임. 적분은 픽스되지 않은 나머지 후보들에 대해서만 적용함.

기대 RIS 가중치

이제 RIS의 PDF도 정의했겠다, RIS 가중치 W(x, z)의 기대값이 PDF의 역수임을 보이도록 하면 됨. 우선 이걸 구하려면 조건부 기대값을 적용해야함. 어떤 출력 표본 y가 주어졌을 때, 평균 가중치가 무엇인가? 즉, x_z = y인 x와 z에 대한 W(x, z)의 기대값을 구하고 p(y)로 나눠준 x_z = y 시행의 확률 밀도를 구하면 됨:

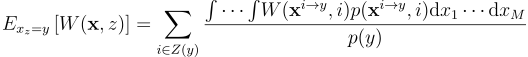
ExpectationOfRisWeight

부록 A에서 이 표현식이 다음과 같이 간략화 됨을 보임:

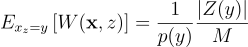
SimplifiedExpectationOfRisWeight

즉, 두 가지를 알 수 있음:

target 함수가 0이 아닐 때, 모든 후보 PDF가 0이 아니라면 |Z(y)| = M임
RIS 가중치가 곧 RIS PDF의 역수의 무편향 추정량이 됨

만약 PDF가 피적분함수의 어떤 영역에서 0이라면 |Z(y)|/M < 1이므로 PDF의 역수는 언제나 과소추정될 것임. 즉, 기대값이 실제 적분값보다 더욱 어두워지는 쪽으로 편향이 발생함.

4.3. 무편향 RIS

RIS 가중치를 수정해주면 편향성을 없앨 수 있음. 1/M을 곱하는 대신, 어떤 가중치 m(x_z)을 곱해주는 것임:

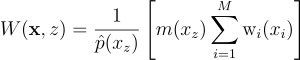
UnbiasedStochasticWeight

위에서처럼 W의 기대값을 계산해보면:

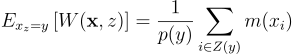
UnbiasedExpectationOfRisWeight

즉, 무편향 추정량은 그냥

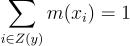
UnbiasedEstimatorRequirement

만 만족하면 됨.

순진한 방법

그럼 그냥 균등 가중치라고 생각하고 m(x_z) = 1 /

Z(x_z)

로 둘 수도 있음. 즉, 후보의 개수 M으로 나누는게 아니라 해당 위치에서 0이 아닌 PDF를 갖는 후보의 수로 나누는 것임.

이러면 편향성은 해결되는데 PDF 역수의 추정량에서 문제가 발생할 수도 있음. 후보 PDF가 0은 아닌데 거의 0에 가깝다고 가정하면, 어쨋든 RIS 추정량 자체는 무편향성을 띠겠지만, RIS PDF 역수의 추정량은 상당히 노이지할 것임.

MIS와 합치기

다행히도 아래 예시와 같이 가중치 m(x_z)을 아무거나 고를 수 있음:

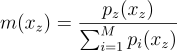
BalanceHeuristicOfCandidatePdfs

즉, 후보 PDF들의 균형 휴리스틱임. 이를 통해 편향성도 해결, 노이즈도 해결할 수 있음.

4.4. 무편향 재사용을 위한 실용적인 알고리듬

이제 편향성을 해결한 식을 재사용 알고리듬(알고리듬 5)에 적용하면 됨. 편향성 자체는 여러 저장소를 합칠 때(알고리듬 4) 발생함: 픽셀 q가 이웃에서 저장소 r_i를 가져올 때, 각 저장소는 표본 r_i.y만큼 기여함. 근데 이 표본의 PDF가 0이면서 또 q의 피적분함수는 0이 아닐 수도 있음! 예를 들어 반구 밑에 있는 후보들은 보통 버려지지만, 이웃 픽셀의 경우 서로 다른 orientation의 평면 법선을 가질 수도 있어 q에는 0이 아닌 contribution을 줄 수 있는 표본들을 버릴 수도 있음. 우리 알고리듬도 유사하게 재사용의 첫 단계에서 가려진 표본들을 버림(즉, PDF가 0이 됨). 그러나 이 픽셀에서 가려져 있다고 해서 이웃에서도 가려져 있다는 보장은 없음. 즉, 이걸 버리면 편향이 발생함.

각 표본 r_i.y은 재사용의 결과이고, 이 표본의 실제 PDF가 뭔지는 모름. 그러나 실제 PDF가 0일 때 이 PDF를 근사한 것도 0에 가깝다는 것만 알면 이걸로 무편향 가중치를 구하면 됨. 픽셀 q_i마다 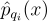ApproximationToRealPdfOfSamplesAtQi 를 근사 PDF로 사용하도록 함. 왜냐면 실제 PDF가 0일 때 이 근사도 0이기 때문임. 만약 가시성 재사용을 ㄱ수행한다면 추가적으로 x가 q_i에서 가려져있는지 여부도 확인하여 PDF를 0으로 설정해줌.

다음은 무편향 저장소 혼합(균등 가중치 사용) 의사 코드임:

알고리듬 6: 다중 저장소 무편향 혼합

입력: 저장소 r_i와 해당 저장소의 출신 픽셀 q_i
출력: 입력 저장소의 무편향 혼합

function combineReservoirsUnbiased(q, r_1, r_2, …, r_k, q_1, …, q_k)
  Reservoir s
  foreach r ∈ {r_1, …, r_k} do
    s.update(r.y, phat_q(r.y) · r.W · r.M)
  s.M ← r_1.M + r_2.M + … + r_k.M
  Z ← 0
  foreach q_i ∈ {q_1, …, q_k} do
    if phat_q_i(s.y) > 0 then
      Z ← Z + r_i.M
  m ← 1/Z
  s.W = (1/(phat_q(s.y))) · (m · s.w_sum) // 무편향 가중치 W(x, z)
  return s

MIS 버전은 마찬가지로 하면 됨.

무편향 버전의 단점은 훨씬 더 비싸다는 것임. 만약 가시성 재사용을 적용한다면 phat_q_i에는 가시성도 포함되므로 추가적인 그림자 광선을 쏴야함. 즉, 공간 재사용의 경우 k 개의 추가적인 광선을 추적해야한다는 것임(이웃 당 하나).

이렇기에 편향 버전과 무편향 버전 둘 다 이 논문에서 제시하는 것임.

5. 설계 및 구현 세부사항

GPU 기반 실시간 렌더링 시스템에 구현.

후보 생성

광원 삼각형의 power에 따라 중요도 표집을 하고, 선택된 삼각형에 대해 균등하게 점 x를 생성(즉, p(x) ∝ L_e(x))하여 M = 32 개의 초기 후보를 생성함. 만약 환경 매핑을 쓴다면, 25%의 후보는 환경 맵에서 중요도 표집을 해서 생성해주면 됨. 이건 alias table을 활용해서 가속화해줄 수 있음. 추가적으로 광원 삼각형에 VPL을 활용해보았는데, 약간 visual artifact가 발생하긴 했는데, 실시간 성능은 엄청 좋았다고 함.

Target PDF

알고리듬의 재사용 단계에서는 표본을 target PDF에 따라 가중치를 줌. 여기서는 그림자가 지지 않은 경로 contribution 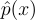TargetPdf ∝ ρ · L_e · G를 각 픽셀의 target PDF로 사용함. 장면의 모든 기하에 대해서는 통일된 material 모델을 활용함. 이 모델은 diffuse 람베르트 substrate 위에 dielectric GGX microfacet 계층이 있는 모델임.

이웃 선택

공간 재사용 때 사전에 정의된 이웃을 사용하니 생각보다 별로였고, 현재 픽셀을 기준으로 30 픽셀 반지름 범위 내에 k = 5(무편향 알고리듬에선 k = 3) 개의 이웃 픽셀을 무작위로, 저불일치 수열을 통해 뽑음. 계층적 À-Trous 표집도 몇 artifact가 생기는 대신 괜찮은 성능을 보이긴 했음. 시간 재사용의 경우 모션 벡터를 통해 현재 픽셀을 직전 프레임으로 옮겨서 구한 픽셀로 시간 재사용을 수행하였음.

편향 알고리듬의 경우 서로 기하성/material성이 다른 이웃에서의 후보를 재사용할 경우 편향성이 높아지므로 그러한 픽셀은 무시하도록 간단한 휴리스틱을 추가했음: 카메라로부터의 거리, 현재 픽셀과 이웃 픽셀의 법선 간의 각도를 통해 특정 기준치를 넘으면(현재 픽셀의 깊이의 10%, 각도는 25˚) 무시하도록 함. 시간 재사용은 n = 2(무편향 알고리듬의 경우 n = 1) 개의 공간 재사용 단계를 사용함.

평가 표본 수

알고리듬 5에서는 N = 1, 즉 단일 표본을 가정했음. 여러 표본을 사용할 경우, 그냥 여러 번 적용한 다음 결과의 평균을 써주면 됨. 무편향 알고리듬의 경우 interactive 프레임레이트를 보장하려면 N = 1, 무편향 알고리듬은 N = 4임.

저장소 저장 및 시간 가중치

각 픽셀에선 오로지 픽셀의 저장소 정보만 저장함: 선택한 표본 y, 픽셀에 기여한 후보수 M, 확률 가중치 W. N > 1이면 여러 개의 y, W를 저장하면 됨. 시간 재사용의 경우 후보의 수 M은 이론상 무한대가 될 수 있지만, 재표집할 때 시간 표본들의 가중치가 과도하게 커지게 됨. 그러므로 직전 프레임의 수 M을 현재 프레임의 저장소 M의 최대 20 배로 설정하여 M이 무한대로 커지는 것도 막고, 시간 정보의 영향에도 한계를 줄 수 있음.

6. 결과

생략

7. 관련 연구

다중 광원 표집Many-light sampling

경로 재사용 및 공간 상관관계Path reuse and spatial correlation

VPL
광자 매핑
(Ir)radiance 캐싱
양방향 경로 추적법
마르코프 연쇄 몬테 카를로 (MCMC) 광전달 알고리듬

재표집Resampling

연쇄 몬테 카를로 (SMC) 방법

비율 & 가중치 추정량Ratio & weighted estimator

가중치 균등 표집weighted uniform sampling(WUS)
가중치 중요도 표집weighted importance sampling(WIS)

(가중치) 저장소 표집(Weighted) reservoir sampling

디노이징/복원Denoising/reconstruction

8. 결론

8.1. 한계 및 향후 연구

결국 픽셀 간의 상관관계에 기반하기에 disocclusion, 불연속적 light, 높은 기하 복잡도, 빠르게 움직이는 빛 등이 발생하는 경우에는 잘 안 됨.

또한 이미지 버퍼를 사용하므로 빠르고, 간단하고, 메모리도 효율적으로 사용하지만 결국 모든 작업은 카메라 경로의 첫번째 정점(즉, 최초 충돌점)에서만 발생하며, 이걸 최초 충돌 이후의 직접광이나 전역광으로 확장하기가 애매함. 이걸 screen-space에서 벗어나게 하는게 중요한 향후 연구일 수도. 특히 시공간 재표집 알고리듬을 world-space 자료구조로 확장하는거, 경로 공간 해싱 등의 알고리듬 사용하는 것처럼하면 괜찮을 듯. 아니면 경로 재사용 알고리듬이랑 합쳐서 써도 될 듯.

Latex

DirectionOmega

\vec{\omega}

ReflectedRadianceL

L{\left(y, \omega \right )} = \int_{A}{\rho{\left(y, \vec{yx} \leftrightarrow \vec{\omega} \right )}L_{e}{\left(x \rightarrow y \right )}G{\left(x \leftrightarrow y \right )}V{\left(x \leftrightarrow y \right )}\textrm{d}A_{x}}

SimplifiedReflectedRadianceL

L = \int_{A}{f{\left(x \right )}\textrm{d}x}

IntegrandF

f{\left(x \right )} \equiv \rho{\left(x \right )}L_{e}{\left(x \right )}G{\left(x \right )}V{\left(x \right )}

ImportanceSampling

\left \langle L \right \rangle^{N}_{\textrm{is}} = \frac{1}{N}\sum^{N}_{i=1}{\frac{f{\left(x_{i} \right )}}{p{\left(x_{i} \right )}}} \approx L

MultipleImportanceSampling

\left \langle L \right \rangle^{M, N}_{\textrm{mis}} = \sum^{M}_{s=1}{\frac{1}{N_{s}}\sum^{N_{s}}_{i=1}{w_{s}{\left(x_{i} \right )}\frac{f{\left(x_{i} \right )}}{p_{s}{\left(x_{i} \right )}}}}

SingleSampleRisEstimator

\left \langle L \right \rangle^{M, 1}_{\textrm{ris}} = \frac{f{\left(y \right )}}{\hat{p}{\left(y \right )}} \cdot \left(\frac{1}{M} \sum^{M}_{j=1}{\textrm{w}{\left(x_{j} \right )}} \right )

NSampleRisEstimator

\left \langle L \right \rangle^{M, N}_{\textrm{ris}} = \frac{1}{N} \sum^{N}_{i=1} \left( \frac{f{\left(y_{i} \right )}}{\hat{p}{\left(y_{i} \right )}} \cdot \left(\frac{1}{M} \sum^{M}_{j=1}{\textrm{w}{\left(x_{ij} \right )}} \right ) \right)

TargetPdfForPixelQ

\hat{p}_{q}

SumOfRisWeights

\sum^{M}_{i=1}{\textrm{w}{\left(x_{i} \right )}}

WrsWeightsProbability

P_{i} = \frac{\textrm{w}{\left(x_{i} \right )}}{\sum^{M}_{j=1}{\textrm{w}{\left(x_{j} \right )}}}

ReservoirReplacementProbability

\frac{\textrm{w}{\left(x_{m + i} \right )}}{\sum^{m + 1}_{j=1}{\textrm{w}{\left(x_{j} \right )}}}

XiRemainingInReservoirProbability

\frac{\textrm{w}{\left(x_{i} \right )}}{\sum^{m}_{j=1}{\textrm{w}{\left(x_{j} \right )}}}\left(1 -  \frac{\textrm{w}{\left(x_{m + i} \right )}}{\sum^{m + 1}_{j=1}{\textrm{w}{\left(x_{j} \right )}}}\right ) = \frac{\textrm{w}{\left(x_{i} \right )}}{\sum^{m + 1}_{j=1}{\textrm{w}{\left(x_{j} \right )}}}

TargetDistribution

\hat{p}{\left(x \right )} = \rho{\left(x \right )}L_e{\left(x \right )}G{\left(x \right )}

NeighboringPixelTargetPdf

\hat{p}_{q'}

NeighboringTargetPdfFactor

\frac{\hat{p}_{q}{\left(r.y \right )}}{\hat{p}_{q'}{\left(r.y\right)}}

ResultingTerm

\frac{\hat{p}_{q}{\left(r.y \right )}}{\hat{p}_{q'}{\left(r.y\right)}} \cdot r.\textrm{w}_{\textrm{sum}}

ResultTermSuccinct

\hat{p}_{q}{\left(r.y \right )} \cdot r.W \cdot r.M