ReSTIR GI: 실시간 경로 추적을 위한 경로 재표집 (revisited) (2022.10.20)

Home

• Yaobin Ouyang, NVIDIA.
• Shiqiu Liu, NVIDIA.
• Markus Kettunen, NVIDIA.
• Matt Pharr, NVIDIA.
• Jacop Pantaleoni, NVIDIA.

초록

요즘에 GPU로 광선 추적을 가속화할 수 있긴 하지만, 그래도 실시간으론 겨우 몇 개의 광선 밖에 추적을 못 함. 그렇기 때문에 디노이저가 아무리 좋아도 문제가 발생할 수 밖에 없음. 최근 ReSTIR 알고리듬이 잘 되긴 하는데, 간접광 전용 알고리듬도 필요함.

평행성이 높은 GPU 구조에 적합한, 간접광을 위한 효과적인 경로 표집 알고리듬을 소개하도록 함. ReSTIR의 screen-space 시공간 재표집 원칙에 기반하여 경로 추적으로 얻을 수 있는 다중 튕김 간접광 경로를 재표집함.

1. 도입

경로 추적법의 장점: 유연함, 일반적임. 즉, 하나의 방정식으로 싹 다 처리할 수 있으니 실시간 렌더링에서 눈독을 들일만함.

역자: 실시간 렌더링에서는 직접광은 tiled shading, clustered shading 등의 lighting culling을 가미한 deferred/forward rendering으로 처리하고… 간접광은 ambient occlusion, environment mapping 등으로 처리하고… 그림자는 shadow mapping으로 처리하고… 등등

근데 이게 경로 추적이 여간 비싼게 아니라서 실시간에서 잘 쓸 수가 없음. (역자: 2021년 기준) 최대 픽셀 당 열 몇 개 수준? 물론 SVGF 알고리듬이나 신경망을 사용한 알고리듬처럼 좋은 디노이징 알고리듬이 있긴 한데, 어쨋든 애초에 광선을 잘 표집을 해서 최대한 장면의 조명에 대한 정보를 많이 주는게 좋음.

여기선 경로 추적법으로 다중 튕김 전역 조명(GI)을 통한 이미지의 품질을 극대화하는데에 집중함. 간접광 표집의 효율성을 높여서 경로 추적을 통한 전역 조명을 실시간에 가능케 하도록 함. 이를 위해 직접광을 표집하는데 쓰였던 RIS + RS(저장소 표집reservoir sampling) = ReSTIR 알고리듬을 적용함.

ReSTIR에서 초기 표본(후보)을 global light space에서 뽑는 것과는 다르게, 우리의 알고리듬에서는 초기 표본을 shading할 지점의 지역 구 위의 한 방향 공간에서 뽑음. 이 방향으로의 광선을 추적하면 장면의 한 표면 위의 점이 나올 것이고, 그 지점에서 초기 표본의 지점으로 산란되는 빛의 양으로 RIS 가중치를 결정함. 이 지점을 시공간적으로 재표집하면 장면의 간접광에 근사하는 분포로부터 가중치가 부여된 표본을 생성하게 되어 오류가 상당히 줄어 들을 것임.

여기서 저장소와 표본을 저장할 모든 자료 구조는 단순 screen-space 버퍼임.

2. 이전 연구

• RIS, Talbot et al.
• ReSTIR, Bitterli et al.
• RS, Vitter, Chao.

간접광이 직접광보다 더 어려운 이유: 적분 영역이 더 복잡하고, 고차원임

그래서 일반적으로는 경로의 각 정점마다, 다음 방향을 지역 BSDF에 잘 맞는 분포에 따라 중요도 표집을 함. 간접광의 다양성이 적으면 BSDF 표집이 잘 되긴 하는데, 엄청 세지만 또 영역은 좁은 간접광이 있을 땐 잘 안 됨.

여기에선 시간(프레임)적으로, 공간(픽셀)적으로 경로를 표집하고, 이를 재사용함. 재사용를 재사용하는 방법 예로부터 가상점광Virtual Point Light(VPL) 등이 사용 되었음. VPL에선 광원으로부터 나온 빛이 최초로 충돌한 정점에서부터의 다음 경로를 표본으로 삼아, 이 정점을 마치 가상의 광원으로 간주하게 됨.

Bekeart et al.에서 사용한 좀 더 일반적인 하위 경로 재사용 방법이 있는데, 이 논문은 여기에서 많은 아이디어를 얻음. 사실상 같은 정점 연결 방법을 사용하면서도 ReSTIR 저장소 표집과 병합 알고리듬을 사용하여 복잡한 추가적인 자료구조 없이 재사용한 하위 경로들을 선택하고 가중치를 부여함. 원래 Bekeart et al.의 논문에서는 O(M²)이 걸렸는데, 우리의 ReSTIR 기반 알고리듬은 임의의 재사용 패턴에 대하여 O(M)임.

3. 배경

결국 실시간 렌더링의 근본적인 문제는 렌더링 방정식 해결:

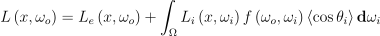
(1)

• L: 나가는 방향의 radiance
• L_e: 발산하는 radiance
• Ω: 표면 법선을 기준으로 하는 방향들로 이루어진 반구
• L_i: 들어오는 방향의 radiance
• f: BSDF
• <cosθ_i>: 방향 ω_i와 표면 법선이 이루는 각 θ_i의 코사인 항. 음수는 0으로 처리함
• dω: 입체각 변화량

participating 매질을 무시한다면 “들어오는 radiance L_i“는 다음과 같이 “지점 x에서 방향 ω_i로 광선을 쏘았을 때 처음으로 충돌하는 표면으로부터 나가는 radiance”로서 표현 가능:

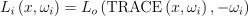
(2)

여기서 TRACE 함수란 x에서 방향 ω_i로 광선을 쏘았을 때 처음으로 충돌하는 표면 위의 점을 반환함.

전통적인 몬테 카를로 방법에서 사용하는 추정량:

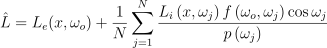
(3)

• N: 독립 표본의 수
• p(ω_j): 표본을 뽑은 PDF

RIS를 통해 직접적으로 표본을 뽑기가 어려운 분포를 근사해줄 수 있음.

1단계: source 분포 p(y)로부터 M 개의 후보 y = y₁, …, y_M 뽑음.
2단계: target PDF 로부터 y에서 한 표본 z를 재표집함.

이때 z는 다음 확률에 의해 뽑음:

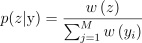
(4)

위의 확률은 가중치에 따른 결과임:

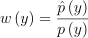
(5)

이를 통해 ∫f(x)dx의 무편향 추정량은 다음과 같은 RIS 추정량으로 표현 가능:

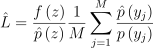
(6)

target PDF가 p보다 더 피적분함수에 잘 맞으면, RIS는 오류를 줄여줌.

Bitterli et al.이 보였듯, WRS를 통해 RIS를 좀 더 효율적으로 GPU에서 구현해줄 수 있음. 이 논문에서도 마찬가지로 WRS를 적용하며, 저장소에서 저장한 표본 z의 가중치 W를 마찬가지로 저장함:

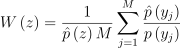
(7)

RIS 추정량은 다음과 같이 단순화 할 수 있음:

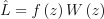
(8)

알고리듬 1: WRS

 1: class Reservoir
 2:     Sample z
 3:     w ← 0
 4:     M ← 0
 5:     W ← 0   // 7번식
 6:     procedure Update(Sample s_new, w_new)
 7:         w ← w + w_new
 8:         M ← M + 1
 9:         if random() < w_new / w then
10:             z ← s_new
11:     procedure Merge(Reservoir r, phat)
12:         M_0 ← M
13:         Update(r.z, phat * r.W * r.M)
14:         M ← M_0 + r.M

4. ReSTIR GI

원래 ReSTIR 논문에서는 초기 표본을 빛 표집으로 함. 즉, 광원들을 power에 따라 뽑은 다음, 뽑힌 광원들을 광원 표면에 대해 균등하게 표집하는 source PDF p(x)를 바탕으로 적용함. Target PDF 의 경우는 그림자가 지지 않은 반사 radiance, 즉 발산하는 radiance * BSDF * 기하항으로 삼음.

ReSTIR으로 간접광 표집하려면 우선 간접광에 contribute하는 방향을 표현할 수 있어야 함. 근데 공간 상의 서로 다른 지점에서 시공간 재사용을 해야하니까, 지역 반구 상의 방향을 표현하는 단위 벡터는 좋은 표현 방법은 아닌 듯함. 차라리 표면 위의 한 지점과, 광선으로 산란되어 오는 radiance를 연계해서 보도록 함.

우선 가시점visible point이란 카메라가 어떤 장면을 바라볼 때 각 픽셀마다 보이는 표면의 지점을 의미함. 이 가시점에서 우선 무작위로 한 방향을 표집해보자. 이 방향으로 광선을 쏘았을 때 처음으로 충돌하는 지점을 바로 표본점sample point이라 부를 것임. 이렇게 표본을 생성한 다음엔 재표집을 진행하고 각 가시점마다 shading을 진행함.

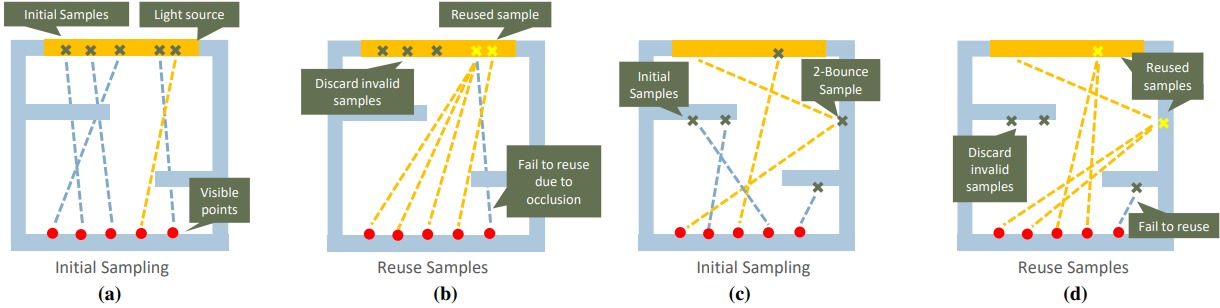
알고리듬은 총 세 개의 이미지 크기의 버퍼를 저장함:

• 초기 표본 버퍼: Sample형의 초기 표본을 저장하는 버퍼
• 시간 저장소 버퍼: 직전 프레임에서 생성한 표본에 WRS를 적용한 표본을 받아들이는 Reservoir의 버퍼
• 공간 저장소 버퍼: 이웃 픽셀에 WRS를 적용한 표본을 받아들이는 Reservoir의 버퍼

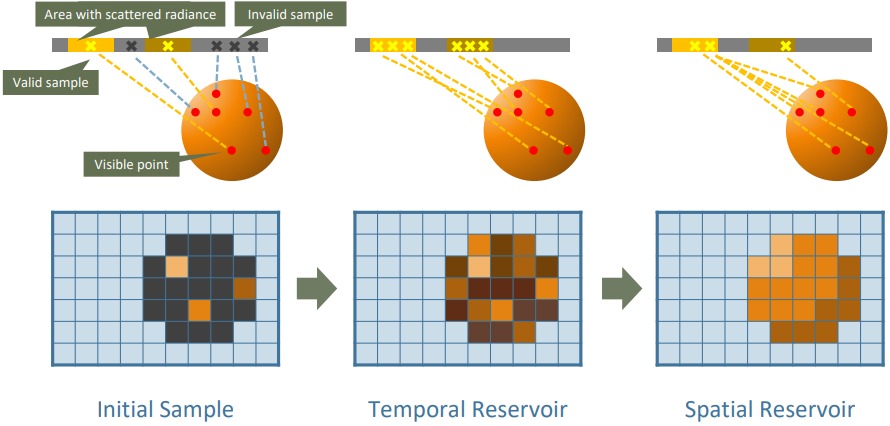
4.1. 표본 생성

알고리듬의 첫번째 단계는 각 가시점마다 새 표본점을 생성하는 것임. 각 가시점의 위치, 표면 법선을 포함한 G-버퍼를 입력으로 받음. 물론 광선 추적을 통한 V-버퍼도 가능.

픽셀 q와 이에 대응하는 가시점 x_v가 주어졌을 때, source PDF p_q(ω_i)에 따라 방향 ω_i을 뽑은 뒤, 이 방향으로 광선을 추적하여 표본점 x_s를 얻게 됨. source PDF는 균등 분포일 수도, 코사인 가중치 분포일 수도, 가시점의 BSDF에 기반한 분포일 수도 있음.

각 표본점에서는 이 표본점에서 가시점으로 나가는 radiance L_o(x_s, ω_o)를 구해야함. 이때 ω_o는 가시점으로의 단위 방향임. 이 radiance 값은 여러 가지로 구할 수 있지만, 이 논문에선 각 정점마다 몬테 카를로 방법 + 후사건 추정Next Event Estimation(NEE) + MIS를 사용함. 만약 직접광도 radiance 추정량에 포함시킨다면, 단일 튕김 전역 조명으로 간주하고 처리함. 즉, n 튕김 경로 추적은 곧 n + 1 튕김 전역 조명임.

알고리듬 2: 초기 표본

1:  for each 픽셀 q do
2:      G-buffer로부터 가시점의 위치 x_v와 법선 n_v 구하기
3:      Source PDF p_q를 활용하여 광선을 쏠 방향 omega_i 표집하기
4:      광선 추적하여 표본점의 위치 x_s와 법선 n_s 구하기
5:      x_s에서 나오는 radiance L_o 추정하기
6:      InitialSampleBuffer[q] ← Sample(x_v, n_v, x_s, n_s, L_o)

4.2. 재표집 및 Shading

따끈 따끈한 초기 표본을 얻은 다음엔 시공간 재사용을 적용함. 이때 사용하는 target 함수는 다음과 같음:

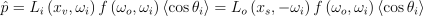
(9)

보면 알겠지만 BSDF, 코사인항 등을 포함하고 있음. 근데 걍 간단하게:

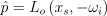
(10)

이렇게만 해도 잘 됨. 제일 최적인 함수는 아니어도, 공간 재사용할 땐 도움이 됨. 이게 어떤 특정 표본들을 유지시켜주는데, 이 표본들이 정작 자기를 생성한 픽셀 말고, 다른 픽셀들에 좀 도움이 됨.

초기 표본 생성한 다음엔 우선 시간 재사용을 적용함. 이 단계에서는 초기 표본 버퍼를 통해 무작위로 시간 저장소를 갱신하게 됨. 5번 식의 RIS 가중치를 구할 땐 source PDF를 방향을 뽑을 PDF로 활용하고 은 10번 식으로 두고 구하면 됨.

알고리듬 3: 시간 재사용

1:  for each 픽셀 q do
2:      S ← InitialSampleBuffer[q]
3:      R ← TemporalReservoirBuffer[q]
4:      w ← phat_q(S) / p_q(S)  // 5번, 9번, 10번 식
5:      R.Update(S, w)
6:      R.W ← R.w / (R.M * phat(R.z))   // 7번 식
7:      TemporalReservoirBuffer[q] ← R

시간 재사용 다음엔 공간 재사용임. 이웃 시간 저장소에서 표본을 가져와서 재표집을 한 다음, 결과를 따로 공간 저장소에 넣음.

참고로 공간 재사용을 할 땐 픽셀 간에 PDF가 다름. 이 논문의 경우 가시점의 위치와 표면 법선을 바탕으로 표집을 하기 때문에 이 차이점을 좀 처리를 해줘야함. 원본 ReSTIR 논문의 경우에는 각 픽셀의 지역적 기하적 특징을 고려하지 않고 빛을 직접적으로 표집했으니 이런 차이를 처리해줄 필요가 없었음. 다시 말해 픽셀 q의 표본을 픽셀 r에서 재사용 한다고 치면, 이 표본에서 사용한 입체각 PDF를 현재 픽셀의 입체각 space로 변환해줘야함. 이를 해주려면 이 변환의 야코비 행렬식으로 나눠줘야 함:

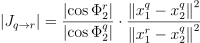
(11)

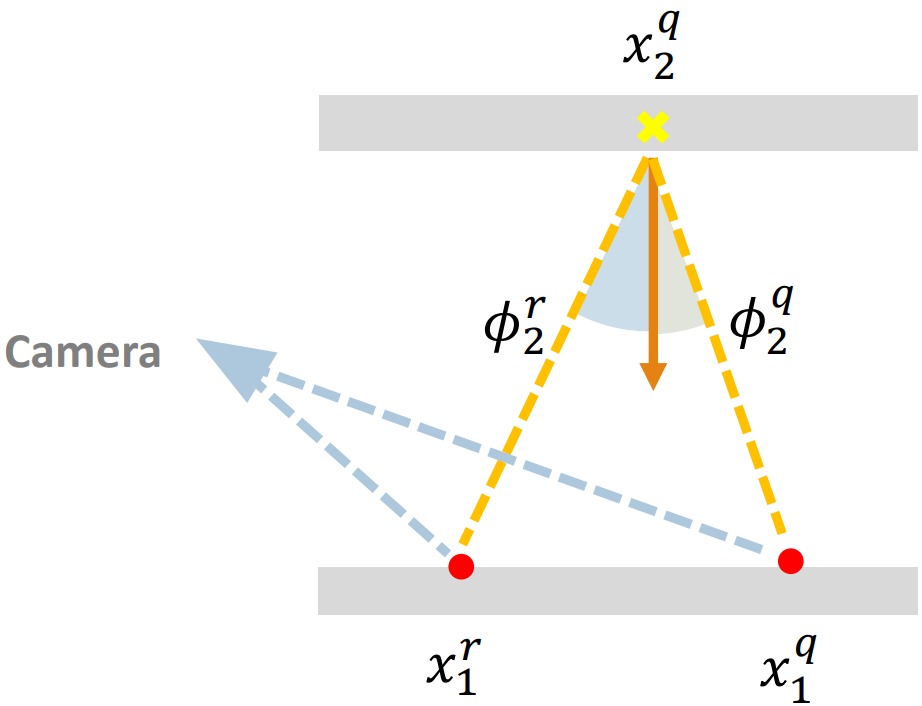
여기서 x₁^q와 x₂^q는 재사용 경로의 첫째와 둘째 정점, x₁^r은 가시점, Φ₂^q와 Φ₁^q는 각각 벡터 x₁^q - x₂^q와 x₁^r - x₂^q가 x₂^q에서의 법선과 이루는 각도를 의미함.

알고리듬 4: 공간 재사용

 1: for each 픽셀 q do
 2:     R_s ← SpatialReservoirBuffer[q]
 3:     Q ← q
 4:     for s = 1 to maxIterations do
 5:         무작위로 이웃 픽셀 q_n 선택
 6:         q와 q_n 간의 기하적 유사성 계산
 7:         if 유사성이 주어진 기준보다 낮다면 then
 8:             continue
 9:         R_n ← TemporalReservoirBuffer[q_n]
10:         q_n → q으로의 야코비 행렬식 계산    // 11번식
11:         phat'_q ← phat_q(R_n.z) / 야코비 행렬식
12:         if R_n의 표본점이 q의 x_v에서 보이지 않는다면 then
13:             phat'_q ← 0
14:         R_s.Merge(R_n, phat'_q)
15:         Q ← Q ∩ q_n
16:     Z ← 0
17:     for each q_n in Q do
18:         if phat_q_n(R_s.z) > 0 then
19:             Z ← Z + R_n.M   // 편향 처리
20:     R_s.W ← R_s.w / (Z * phat_q(R_s.z)) // 7번식
21:     SpatialReservoirBuffer[q] ← R_s

위의 알고리듬에서도 원본 ReSTIR 논문에서처럼 기하적 유사성 검사를 수행해서 표면 법선이 25도 이내, 정규화 깊이가 0.05 이내인지 확인해줌.

재사용 다 끝나면 가시점 x_v에서 간접광에 의한 최종 산란 radiance를 6번식의 RIS 추정량을 통해 구해줌. 이때 공간 저장소 W의 가중치가 f(y) 이외의 모든 요소를 의미하며, 이는 BSDF, 코사인항과 저장소의 표본의 outgoing radiance의 곱임.

4.3. 편향성

ReSTIR처럼 ReSTIR GI 알고리듬도 편향 버전이랑 무편향 버전의 알고리듬이 존재함.

ReSTIR의 경우 공간 재표집을 할 때 픽셀마다 서로 다른 PDF을 사용하다보니 직접광을 표집할 때 편향성이 발생함. 즉, 픽셀 간의 source PDF의 영역이 다르면 편향성이 발생함. 이건 가시성 광선을 추적해서 어떤 source 분포가 최종적으로 선택한 표본을 표집할 수 있는지를 확인하고, 이에 따라 결과에 가중치를 부여해주는 것으로 고칠 수 있음 (알고리듬 4의 18번에서 해주는 테스트가 바로 이거임). 광선 안 쓰고 하는 법도 있음. 픽셀 간 기하 유사성 검사를 해주면 됨.

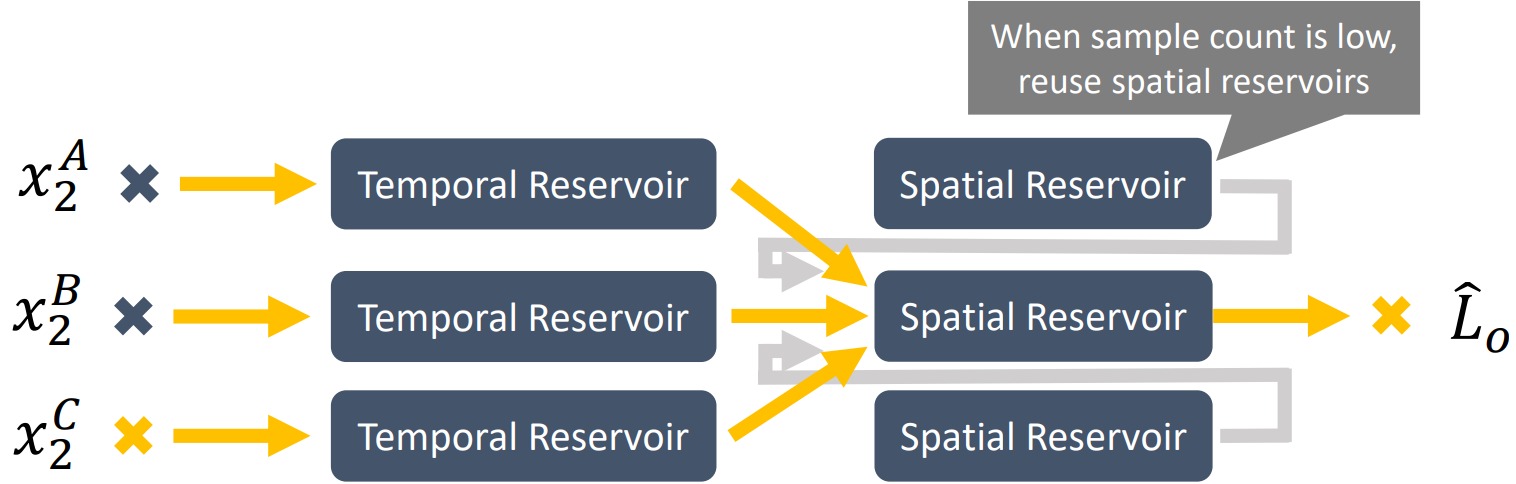
공간 재사용에서 편향성을 줄이는 다른 방법으로는 공간 저장소가 이웃 공간 저장소가 아니라, 이웃 시간 저장소에서만 처리하도록 하는 것임. 이러면 여러 단계의 편향된 표집을 재표집하면서 편향성이 누적되지 않을 것임. 물론 이렇게 되면 가려져 있다가 밖으로 나온 픽셀들은 충분히 많은 표본을 갖지 않을 것이므로 노이즈가 발생할 것임. 이럴 경우를 위해 적은 입력 표본 개수를 갖는 공간 저장소를 사용하여 근처 공간 저장소를 통해 수렴 속도를 개선하도록 함.

만약 source 분포가 각 픽셀의 지역적인 기하적 특성에 의존하게 된다면, 즉 BSDF 표집을 사용하게 되면 편향성이 발생함. 넓이를 기준으로 한 같은 분포라도 서로 다른 픽셀의 입체각에 따라 다른 모양을 갖게 됨. 이런 차이점을 고려 안 하고 이웃으로부터 표본을 재사용하게 되면 편향성이 발생함. 이건 11번식을 통해 해결할 수 있음. 어차피 연산 복잡도도 낮은데 안해줄 이유가 없는?듯.

장면의 내용물(조명, 기하 등)이 바뀌면 시간 재사용할 때 표본점에 저장된 outgoing radiance이 정확하지 않은 값이 될테니까 편향성이 발생함. 게다가 ReSTIR 특성상 밝은 표본을 저장소에 넣으려는 경향성이 있어서 더욱 문제가 커짐. 이러면 장면의 변동사항을 적용하는데 약간의 렉이 걸릴 수 있음. 이걸 처리하기 위해 A-SVGF 디노이징 필터에서 아이디어를 얻은 표본 검증 메커니즘을 사용함. 몇번째 프레임마다 광선을 다시 추적해서 모든 저장소 표본마다 outgoing radiance를 다시 계산해서 적당한 범위 내면 ㄱㅊ, 아니면 저장소를 비워줌(이 단계에서는 처음에 생성한 표본의 수만큼 표집해줘야함! 중요!). 표본 검증의 빈도는 장면이 얼마냐 동적이느냐에 따라 설정해주면 됨.

또다른 시간 재사용에 따른 편향성으로는 처음 표본점이 생성된 이후, 가시점과 표본점 사이에 어떤 가리고 있는 물체가 발생할 때임. 이건 표본 검증을 할 때 그림자 광선을 표본점에서 가시점으로 쏴줘서 처리하면 됨.

5. 구현

Unreal Engine 4과 Falcor에서 구현.

Unreal Engine의 경우:

• 초기 G-Buffer는 래스터화로 생성
• full screen-pass로 각 가시점에서 표본점 생성

Falcor의 경우:

• 광선 추적으로 G-Buffer 생성
• 이후 full-screen pass에서 시공간 재표집
  • 시간 재표집은 모션 벡터에 따라 직전 프레임에 reproject된 픽셀을 사용
  • temporal reprojection fail하면 공간 재표집하기 전에 시공간 저장소 둘 다 리셋함

효율성을 위해 표본점에서 산란 radiance의 방향의 다양성을 무시함. 대신 원래 가시점으로의 방향으로 산란된 radiance를 모든 방향에서 사용, 즉 람베르트 산란을 따라함. 즉, 표본점이 원래 자기를 생성했던 가시점이 아닌 곳이랑 연결되면 표본점의 BSDF가 완전 diffuse하지 않으면 오류가 발생할 수도 있음. 참고로 이렇게 단순화하는게 가시점의 BSDF가 람베르트이거나 이후 간접 경로의 정점들이 람베르트 산란일 필요는 없음

시공간 저장소를 두 개의 버퍼로 두어 공간 재표집할 때 경합 없이 다른 픽셀의 시간 버퍼를 접근할 수 있음. 이러면 간접광을 할 때 한 프레임 정도 렉이 발생하는데, 프레임율만 높으면 큰 문제가 안 됨.

off-chip 메모리의 저장소를 위해 Sample 구조체의 표면 법선은 4 바이트, outgoing radiance는 반정밀도 부동 소수점을 사용함. 각 저장소는 총 48 바이트가 필요함. 이러면 초기 저장소랑 시공간 저장소가 있으니 1080p에서는 G-Buffer를 제외하고는 총 475 MB를 사용함. 프레임마다 저장소에서 데이터 읽는데 대충 570 MB의 대역폭이 필요하고, 메모리에 저장소 갱신하는데 285 MB의 대역폭을 사용함.

실제로는 픽셀에서 매 프레임마다 긴 경로를 표집하면 성능 너무 먹으니까 오로지 25%의 픽셀에서만 다중 튕김 경로를 처리함. 이 25% 픽셀을 무작위로 고르면 낮은 스레드 일관성에 의해 성능이 별로 안 나옴. 그러므로 화면을 64 × 32 픽셀의 타일로 나누고 타일마다 러시안 룰렛을 적용하여 러시안 룰렛에서 탈락한 타일은 단일 튕김 간접광 경로로 렌더링, 즉 표본점에서 직접광만 처리하고, 통과한 타일은 다중 튕김 경로로 처리하지만, 러시안 룰렛의 확률에 따라 가중치를 부여함. 이를 통해 모든 경로의 기대값이 다중 튕김 경로인 것처럼 해줌. 실제로는 시공간 재표집의 확률적인 특성 덕분에 이런 타일 패턴을 잘 숨겨줌.

시간 저장소의 M 값은 30으로 제한하고, 공간 저장소는 500으로 제한하여 특정 표본에 갖혀서 M이 커져도 교체가 거의 안 일어나는 경우를 방지함.

공간 저장소 버퍼의 모든 출력 표본을 어떤 프레임 주기마다 검증함. 초기 표본 단계를 재사용하여 표본 검증을 해서 추가적인 성능 비용이 들지 않도록 함. 표본 검증 프레임 땐 초기 표본 단계에서는 표본 정보를 읽고, 똑같은 광선을 추적해 radiance 값을 검증함. 기본적으로 매 6번째 프레임마다 표본을 검증함.

공간 재표집 알고리듬에서 maxIterations 매개변수가 성능에 상당한 영향을 줌. 실제로 몇 개의 표본만 처리한 저장소는 노이즈가 높고 artifact가 발생하므로 maxIterations를 각 픽셀의 공간 저장소의 표본 개수에 따라 정해줌. 표본의 개수가 공간 저장소의 최대 M 값의 절반보다 적으면, maxIterations를 9로 두고, 그 이외의 경우엔 3으로 둠.

공간 재표집할 때 사용하는 탐색 반지름도 이미지 품질에 영향을 줌. 이웃의 범위를 넓게 설정하면 복잡한 장면에서는 잘 안 될 수도 있음. 여기서는 적응형 탐색 전략을 사용함. 이미지의 화질 10%를 초기 탐색 반지름으로 설정함. 공간 재사용할 때 만약 다른 픽셀의 표본을 재사용할 수 있으면 괜찮은데, 그게 아니라면 반지름을 절반으로 줄이고, 최소 하한선은 3 픽셀임.

6. 결과

(생략)

6.1. 한계점

ReSTIR GI의 비용이 실시간에 사용하기엔 좀 높긴 함. 보통 게임에서는 30 fps 이상의 성능이 나와야하는데, 이러면 전역 조명에는 2ms 정도 밖에 사용을 못 함. 이 경우엔 저장소 버퍼의 화질을 줄일 수도 있지만, 이러면 디테일한 법선 맵이 있을 땐 공간 재사용이 좀 불안정해짐.