몬테 카를로 적분법이란? (2022.10.13)

Home

몬테 카를로 적분법Monte Carlo integration이란 적분값을 직접 구하기 힘들 때, 무작위로 sample을 추출하여 적분값을 추정하는 방법임.

1. 배경 지식 / 확률 복습 시간

확률 변수 X란 어떤 한 랜덤 프로세스에 의해 선택된 값이다.

랜덤 프로세스란 동전 던지기, 주사위 던지기, 내일 비가 올 확률 등 어떤 결과값을 숫자에 매핑하는 프로세스이다.

한 번 직접 결과값과 숫자 매핑을 직접 해보도록 하자:

확률 변수 X란, 동전을 던졌을 때 앞면이 나오면 1이고, 뒷면이 나오면 0인 변수다.

여기서 랜덤 프로세스는 동전 던지기이고, 앞면과 뒷면이라는 결과값을 1과 0이라는 숫자에 매핑하는 것이다!

수학적으로는 보통 Y = f(X)로 작성한다.

또다른 예시로는 주사위 던지기가 있다.

확률 변수 X란, 주사위를 던졌을 때의 그 값이다.

이때 각 랜덤 프로세스의 한 실행을 시행event이라 부른다.

주사위의 경우 1, 2, 3, 4, 5, 6 중 하나의 값이 나오며 이 여섯 가지 경우의 수가 시행들인 것이다. 이때 각 시행 전부 1/6의 확률로 나오게 될 것이다.

그래픽스의 경우 어떤 한 지점으로 들어오는 모든 빛에 대해서 sampling을 하는 것이므로, 어떤 들어오는 빛 Φ_i가 존재할 때, 해당 시행이 발생할 확률 p_i는

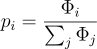
가 된다.

당연히 모든 시행의 확률을 다 더하면 1이 될 것이다.

누적분포함수cumulative distribution function(CDF)란 주어진 확률 변수가 특정 값보다 작거나 같은 확률을 나타내는 함수이다.

예시로 보자면, 주사위를 던졌을 때 2보다 작거나 같은 수가 나올 확률은 전체 여섯 가지 시행 중 두 가지 시행에 해당하므로, 1/6 + 1/6 = 1/3가 된다.

1.1. 연속 확률 변수

당연하겠지만, 렌더링에선 한 점에 대해 들어오는 빛은 무수히 많다. 주사위처럼 이산적으로 셀 수 있는 것이 아니다. 즉, 확률 변수가 연속적일 수 밖에 없다.

우리가 알아야할 매우 중요한 연속 확률 변수는 바로 표준 연속 균등 확률 변수canonical uniform random variable이다. 주로 ξ로 표기한다. 정규 균등 확률 변수는 말로 들으면 매우 어려워보이지만, 그냥 [0, 1) 범위에서 동일한 확률을 갖는 확률 변수이다.

위에서 a = 0, b = 1인 경우가 바로 표준 연속 균등 확률 변수의 확률을 의미하는 함수이다.
퍼블릭 도메인, 링크

이 함수가 중요한 이유는 소프트웨어에서 손쉽게 이 분포로부터 한 변수를 생성할 수 있기 때문이다. 또한, 어떤 임의의 분포에서 샘플을 생성한다고 할 때, 우선 표준 연속 균등 분포에서 샘플을 생성한 수, 적절한 변환을 주어 원하는 분포에서 샘플링한 것처럼 변환시킬 수 있기 때문이다.

연속 확률 변수의 예시를 들어보자도록 하자. 실수 범위 [0, 2]에서 어떤 임의의 값 x를 뽑을 확률이 값 2 - x에 비례한다고 가정하자. 이렇게 되면 x = 0일 확률은 x = 1일 확률의 두 배일 것이다.

위의 개념을 확장한 것이 바로 확률 밀도 함수probability density function(PDF)이다. 즉, 확률 변수가 어떤 값을 갖느냐에 대한 상대적인 확률을 의미한다. PDF p(x)는 해당 확률 변수의 CDF인 P(x)의 도함수이다.

균등 확률 변수의 경우 당연하겠지만 위의 그림에서처럼 p(x)는 상수이다.

PDF는 반드시 양수여야하며, 언제나 정의역에 대하여 적분할 경우 결과값이 1이다.

2. 기대값과 분산

어떤 함수 f의 기대값expected value E_p[f(x)]란 f(x)의 정의역에서 정의된 어떤 분포 p(x)에 대한 함수 f의 평균값이다.

말이 좀 복잡한데, 간단하게 얘기하자면:

만약 동전 던지기를 해서 앞면이 나오면 1, 뒷면이 나오면 0이라는 값을 갖는 확률 변수가 있다고 가정하자. 이 경우 한 번 동전 던지기를 했을 때 나올 확률 변수의 값의 기대값은 얼마인가? 당연히 1도 아니고, 0도 아닐 것이다. 둘이 반반이라는 확률로 나올테니, 대충 우리는 직감적으로 0.5라는 값을 찍게 된다.

반대로, 동전이 한 쪽 면만 무거워서 1/3의 확률로 앞면이 나오고, 2/3의 확률로 뒷면이 나온다면, 우리는 뒷면이 조금 더 나오는 것으로 좀 더 기대할 수 있다. 그렇다면 구체적인 기대값은 얼마가 될 것인가? 당연히 0과 1을 한 선상에 놓고 보면 우리는 0에 좀 더 가깝게 값을 주어야한다. 그렇다면 얼마나 더 가까워야할까? 대충 1은 1/3 만큼 나오고, 0이 2/3만큼 나오니까, 1과 0 사이를 1/3 : 2/3 의 비율로 나눠야하지 않을까? 즉, 우리는 기대값을 자연스럽게 0.66666… 라는 값으로 구하게 된다.

이를 통해 알 수 있는 결론은 두 가지다.

1. 기대값이라는 건 사실상 평균이구나
2. 각 확률 변수의 값과 그 값의 확률을 곱한 것을 전부 더한 것이 기대값이구나

이제 이 사실을 통해 좀 더 복잡한 경우를 구해보자:

한 교실에 롤을 하는 학생 100명을 모았다고 해보자. 이중 5명은 다이아, 10명은 플레, 20명은 골드, 25명은 실버, 20명은 브론즈, 10명은 아이언, 10명은 언랭이라고 해보자.

그럼 우리가 임의로 한 명을 뽑았을 때 대충 그 티어는 어디라고 “기대expected”할 수 있을까? 어떤 티어로 찍어야 최대한 많이 맞출 수 있을까? 보통 이럴 때 우리는 “평균”이라는 개념을 사용하게 된다.

언랭을 0, 브론즈를 1, 실버를 2, 골드를 3, 플레를 4, 다이아를 5라고 매핑을 해보자.

그러면 언랭일 확률은 10%, 브론즈일 확률은 20%, 실버일 확률은 25%, 골드일 확률은 20%, 플레일 확률은 10%, 다이아일 확률은 5%이다.

즉, 기대값 E = 0 * 0.1 + 1 * 0.2 + 2 * 0.25 + 3 * 0.2 + 4 * 0.1 + 5 * 0.05 = 0.1 + 0.2 + 0.5 + 0.6 + 0.4 + 0.25 = 2.05라는 값이 나온다.

기대값 E가 2.05이므로, 대충 이 교실에서 아무나 뽑았을 때 그 학생은 실버일 확률이 높을 것이다. 실제로 실버가 사람이 제일 많기도 하고, 실버를 중심으로 브실골에 학생이 많이 몰려있으니 틀린 추측은 아닐 것이다.

함수의 분산variance(V)이란 어떤 함수가 기대값으로부터의 기대 표준 편차이다. 즉, 다시 말하면 결과가 기대한 것보다 얼마나 벌어져있느냐에 대한 기대값이다.

식으로 표현하면 자연스레 V[f(x)] = E[(f(x) - E[f(x)])²]가 된다.

즉, 분산 값이 작으면 작을 수록 기대값에 대한 오차가 줄어들 것이라는 것은 직관적으로 알 수 있다.

2. 몬테 카를로 추정량

이제 드디어 몬테 카를로 추정량이라는 것을 배울 수 있다.

고등학교 수학 때 배웠던 것처럼, x, y 평면에 정의된 한 함수 f(x)를 x에 대한 범위 [a, b]에 대하여 적분하는 방법은 다음과 같이 표기가 가능하다:

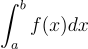
이때 위의 적분을 구하기 위해서 우리는 고등학교 수학 때 구분구적법(리만 합)이라는 것을 배웠다:

By 영어 위키백과의 Icedemon - 이 PNG 컴퓨터 그래픽스는 Gnuplot(으)로 제작되었습니다., 퍼블릭 도메인, 링크

이처럼 적분값을 추정하는 방법의 가장 대표적인 경우가 바로 구분구적법이다. 헌데 우리는 이 구분구적법을 확률 변수라는 안경으로 바라보려고 한다. 사실 우리는 이 함수의 적분값을 범위에 대해 균등하게 나눈 샘플을 갖고 넓이를 구한게 아닐까? 그럼 각 샘플 x_i마다 직사각형의 넓이를 구해서 더해준게 구분구적법이잖아? 그러면 우리가 N 개의 직사각형으로 적분을 추정하고 있다고 가정하면, 각 직사각형의 넓이는 곧

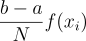
이 된다.

이걸 전부 더해주면 우리는 적분값을 추정할 수 있게 될 것이다:

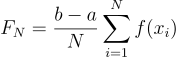
이때 이 값의 기대값은 과연 얼마일까?

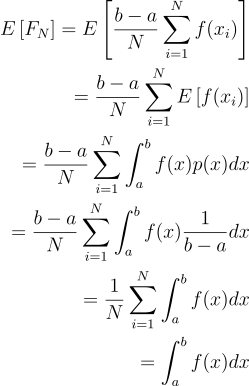
즉, 결국 적분값이 된다!!

근데 생각해보면 어떤 함수의 적분값을 언제나 연속 균등 확률 변수로 구하면 언제나 좋은 결과를 얻을 수는 없을 것이다. 범위를 많이 차지하는 극대점에서는 많이, 극소점에서는 적게 샘플링을 해주면 좀 더 좋은 결과를 낼 수 있는게 아닐까? 이처럼 각 함수별로 더욱 알맞는 확률 분포가 존재할 것이다. 그렇다면 우리는 위의 방법을 어떤 임의의 확률 밀도 함수 PDF에 대해서 일반화해줘야한다:

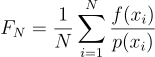
이것이 바로 몬테 카를로 추정량이다!

당연하겠지만, f(x)의 값이 0이 아닐 땐 p(x)는 반드시 0이 아니어야 한다.

변수가 여러 개로 늘어나도 동일하다. 변수 x, y, z에 대하여 적분을 해야한다고 가정해보자:

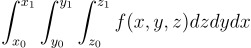
이 경우 확률 변수 X_i = (x_i, y_i, z_i)가 주어진 범위에서 연속 균등하게 분포되어있다면,

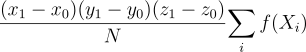
처럼 표현할 수 있을 것이다.

3. 확률 변수 표집

결국 위의 몬테 카를로 추정량을 구하려면 어떤 확률 분포에서 무작위로 표본을 뽑아야한다.

3.1. 역방법

역방법inversion method이란 하나 이상의 균등 확률 변수를 원하는 분포의 확률 변수로 매핑해주는 방법이다.

예를 들어 네 가지 경우의 수가 있다고 가정해보자. 각 경우의 수는 p₁부터 p₄까지의 확률을 갖는다.

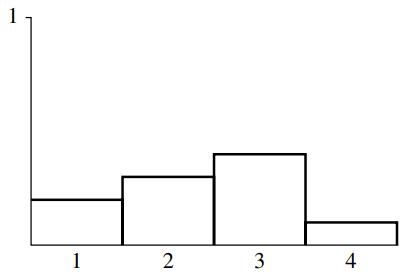
이 분포로부터 한 표본을 뽑으려면 우선 CDF P(x)를 구해야한다.

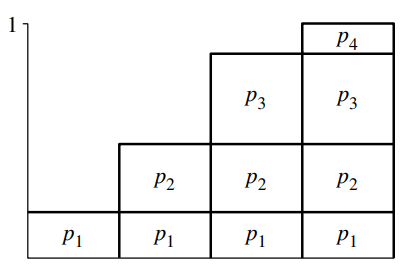
이제 간단하다. CDF P(x)의 결과값, 즉 치역인 [0, 1] 사이에서 연속 균등 확률 변수 값 ξ 하나를 뽑으면 된다.

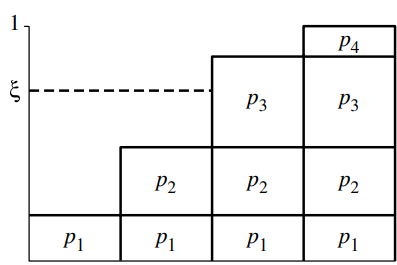
이러면 필연적으로 i번째 확률변수의 확률 p_i와 ξ 값이 서로 충돌하게 된다. 이런식으로 연속 균등 확률 변수 ξ_i에 대하여 p_i에 대응하는 확률 변수 X_i를 선택하게 되면, 자연스럽게 PDF에 알맞게 분포가 나올 것이다.

결국 CDF의 역함수를 구하여, 해당 함수의 입력 변수가 ξ일 때의 출력 변수가 곧 구하려는 확률 변수가 되는 것이다. 그래서 역방법inversion method이라고 부르는 것이다!!

좀 더 구체적으로 보자면:

1. CDF를 구한다:
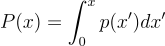
2. 역함수 P^-1(x)를 구한다
3. 균등 확률 변수 ξ를 구한다
4. X_i = P^-1(ξ)를 구한다

3.2. 리젝선 방법

어떤 함수 f(x)의 경우에는 적분이 불가능해 PDF를 구할 수 없거나, CDF의 역함수를 해석학적으로 구할 수 없는 경우가 있다. 이 경우에는 이런 방법 없이도 표본을 생성할 수 있는 방법인 리젝션 방법rejection method를 사용해야한다. 리젝션 방법은 사실상 그냥 과녁에 활 쏘는 방법이다.

예를 들어, 우리가 역방법으로는 처리할 수 없는 어떤 함수 f(x)로부터 표본을 뽑으려고 한다고 하자. 이때 f(x) < c p(x)를 만족하는 PDF p(x)가 어떤 상수 c에 대하여 존재하고, 우리가 p로부터 표본을 뽑는 방법을 알고 있다면:

무한 반복:
    p의 분포로부터 X 뽑기
    만약 ξ < f(X) / (c p(X))라면
        X 반환

사실상 계속해서 (X, ξ)라는 확률 변수 짝을 구하는건데, 점 (X, ξ c p(X))가 f(X)보다 아래에 있으면 OK, 아니라면 다시!를 외치는 방법이다.

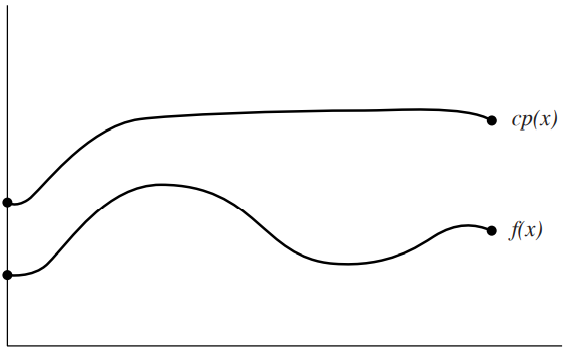
당연하겠지만, c p(x)가 f(x)에 대하여 좀 더 잘 감싸는 형태가 된다면 좀 더 효율적으로 위의 루프가 돌 것이다.

사실상 자주 사용하는 방법은 아니지만, 일단 알아두도록 하자.

4. 분포 간 변환

사실상 역방법도 표준 연속 균등 확률 변수를 변환시켜 다른 분포의 표본으로 만들어준 방법이다. 이를 좀 더 일반화해보도록 하자.

어떤 PDF p_x(x)의 확률 변수 X_i가 이미 주어졌을 때, Y_i = y(X_i)인 새로운 분포에 대한 확률 변수 Y_i가 있다고 해보자.

당연하겠지만 함수 y는 일대일 대응 변환이어야 한다. 일대일 대응 함수라는 것은 결국 y의 도함수의 값은 반드시 전부 0보다 크(y가 단조증가 함수)거나, 0보다 작을(y는 단조감소 함수) 것이다.

즉, 누적분포함수 Pr에 대하여 Pr{Y ≤ y(x)} = Pr{X ≤ x}라는 의미이므로,

P_y(y) = P_y(y(x)) = P_x(x)

라는 의미이다.

만약 y가 단조증가하는 함수(도함수가 0보다 큼)라면,

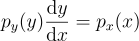
즉,

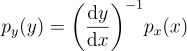
이걸 이제 일반화해주자. y가 단조감소인 경우까지 고려해주면 절대값을 씌워주면 될 것이다:

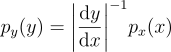
예를 들어 정의역 [0, 1]에 대해 p_x(x) = 2x이고, Y = sin x라고 가정하면, 확률 변수 Y에 대한 PDF는:

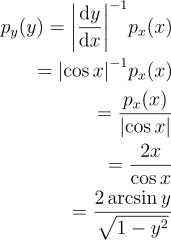
4.1. 다차원 변환

만약 n 차원이라면, 자연스럽게 야코비 행렬을 떠올리면 된다.

만약 n 차원 확률 변수 X에 대하여 PDF p_x(x)가 존재하고, Y = T(X)라고 가정하자. 이때 T는 전단사 함수이다. 이때 PDF는 다음과 같다:

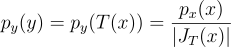
4.2. 극좌표계

x = r cos θ, y = r sin θ이다.

이때 어떤 분포 p(r, θ)에서 표본을 뽑는다면, 이에 대응하는 p(x, y)는 무엇인가?

야코비 행렬을 구해보면:

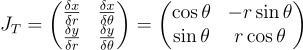
이때 행렬식은 r이므로, p(x, y) = p(r, θ) / r가 된다.

만약 반대로 데카르트 좌표계를 극좌표계로 바꾼다면:

p(r, θ) = r p(x, y)

로 된다.

5.3. 구면좌표계

구면좌표계의 경우:

x = r sin θ cos φ y = r sin θ sin φ z = r cos θ

이고, 이에 대응하는 야코비 행렬의 행렬식은 r²sin θ이므로,

p(r, θ, φ) = r²sin θp(x, y, z)

이다.

이를 solid angle ω에 대한 식으로 바꾸려면

dω = sin θ dθ dφ

이므로,

p(θ, φ)dθ dφ = p(ω)dω p(θ, φ) = sinθp(ω)

가 된다.

5. 다차원 변환을 통한 이차원 표집

우리가 표본 (X, Y)를 뽑을 이차원 joint 확률 밀도 함수 p(x, y)가 주어졌다고 하자. 만약 두 확률 변수가 서로 독립적이라면 이 둘의 곱으로 p(x, y) = p_x(x)p_y(y) 표현해주면 그만이다.

하지만 실질적으로 그런 경우는 거의 없다.

어떤 이차원 확률 밀도 함수가 주어졌을 때, 주변 확률 밀도 함수marginal density function p(x)는 차원 중 하나를 “적분”하여 얻을 수 있다:

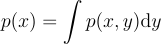
사실상 어떻게 보면 X에 대한 확률 밀도 함수인 것처럼 해석할 수 있게 된다. 정확하게 표현하자면, 이건 모든 가능한 y 값에 대한 평균 밀도가 된다.

조건부 확률 밀도 함수conditional density function p(y

x)는 특정 x가 선택 됐을 때 y에 대한 확률 밀도 함수다:

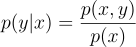
joint 분포로부터의 이차원 표집의 기본은 우선 주변 확률 밀도 함수를 구해서 한 변수를 고정시키고, 이 함수로부터 통상적은 일차원 기법으로 표본을 구하는 것이다. 이 표본을 구한 다음엔, 조건부 확률 밀도 함수를 활용하여 표본을 구하는데, 이번에도 통상적인 일차원 기법으로 표본을 구하게 된다.

5.1. 반구 균등 표집하기

예를 들어, 어떤 한 반구에서 solid angle에 대하여 균등하게 한 방향을 골라보도록 하자. 균등하다는 것은 확률 밀도 함수가 c라는 상수를 갖게 된다는 것이다. 즉, c = 1/(2π)이다.

결국 PDF는 p(ω) = 1/(2π)이며, 이를 구면좌표계로 변환하면 p(θ, φ) = sin θ / (2π)가 된다. 즉, 이 경우엔 두 변수 θ와 φ는 분리가 가능하다는 뜻이다! 어쨋든 계속해서 주변부와 조건부 확률 밀도 함수로 계속해서 구해보도록 하자.

우선 θ에 대하여 표본을 뽑아보도록 하자. θ에 대한 주변부 확률 밀도 함수 p(θ)를 우선 구해보자:

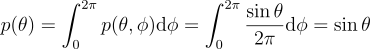
이제 φ에 대한 조건부 확률을 구해보도록 하자:

어라? φ는 보니까 균등 확률을 갖고 있다. 직관적으로 이해해보자면, 이러면 반구의 대칭성이 설명이 된다. 자 이제 일차원 기법으로 각 PDF를 순서대로 표집해보자.

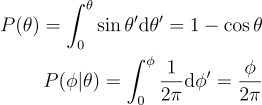
이제 역방법을 적용해보자. 이때 ξ를 1 - ξ로 대체해서 사용해보자 (어차피 균등해서 상관이 없다!).

θ = cos^-1ζ₁
φ = 2πζ₂

이걸 데카르트 좌표로 다시 변환하면:

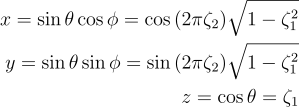
5.2. 단위 원판 표집하기

반구랑 비슷해보여도, 직관적으로 풀면 십중팔구 틀리기에 조금 생각을 해봐야하는 경우이다. 가장 대표적인 실수가 바로 r = ζ₁, θ = 2πζ₂로 두고 푸는 경우이다. 사실 생각해보면, 이럴 경우 원점과 가까운 표본이 더 자주 나오게 될 것이다.

즉, 넓이에 대하여 균등하게 표집을 해야 하므로, 우선 p(x, y)가 상수이고, 그 값이 1/π라는 것은 명백하다 (1 / 단위 원판의 넓이 (θ)). 이를 극좌표계로 치환하면 p(r, θ) = r/θ가 된다. 이제 위와 같이 주변부/조건부 콤보를 먹여보자.

p(r) = 2r
p(θ | r) = 1/(2π)

반구에서와 마찬가지로, 원도 대칭이므로 조건부가 균등하다는 것을 알 수 있다. 이제 이걸 적분하여 P(r)을 구하고, 그 역함수를 구하고, 이를 θ에 대한 P(θ)을 구하고, 그 역함수를 구하면 그 결과를 알 수 있게 된다:

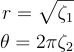
5.3. 코사인 가중치 반구 표집

사실상 반구에서 균등하게 표집하는 것보단 코사인 가중치가 붙은 반구에 표집을 하는게 좀 더 자주 발생할 것이다.

즉, p(ω) ∝ cos θ 라는 것인데, 이를 구면좌표계로 변환하여 얼마나 비례하는지 구해보도록 하자:

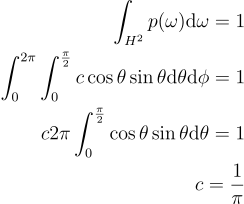
즉,

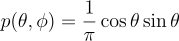
가 된다.

위에서 했던 방법과 마찬가지로 주변부 / 조건부 콤보를 써줘도 되지만, 여기선 맬리 방법Malley’s method을 사용하도록 하자. 맬리 방법의 경우 단위 원판에서 한 점을 균등하게 뽑은 다음, 원판 위에 해당 점을 투영시켜 얻은 점의 방향을 뽑는 것이다. 이때 얻게 되는 분포는 곧 코사인 분포라는 것이다.

6. 중요도 표집

우리는 왜 몬테 카를로 방법에서 분산을 줄여아할까? 이는 확률 변수에 대한 추정치의 정밀도를 높여야 하기 때문이다. 대표적인 방법 중 하나가 stratified sampling과 중요도 표집importance sampling이 있다.

IS의 기본적인 개념은 몬테 카를로 추정량

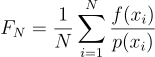
에서 표본들이 함수 f(x)랑 비슷한 분포 p(x)에서 나올 수록 더욱 빠르게 수렴한다는 점에서 시작한다. 즉, 피적분 함수의 값이 상대적으로 높은 곳에 좀 더 집중할 수록 더 효율적으로, 정확하게 추정을 할 수 있다는 것이다.

예를 들어 렌더링 방정식을 추정한다고 할 때, 표면 법선과 거의 수직인 방향의 표본을 하나 뽑는다고 가정해보자. 이러면 코사인 항이 거의 0이 되니까 BSDF 구하고, 광선 쏴서 들어오는 radiance 구하고… 이거 다 헛고생 되는 것이다. 즉, 방향이 좀 더 피적분 함수의 여러 항들(BSDF, 들어오는 조명 분포 등)이랑 비슷한 분포로 뽑혔다면 좀 더 효율적으로 추정할 수 있을 것이다.

피적분 함수와 유사하게 생긴 확률 분포에서 확률 변수를 뽑기만 한다면 일단 분산은 줄어든다.

그래서 그런 확률 분포가 도대체 뭐냐? 생각보다 구하기가 어렵지 않다. 허나 피적분 함수가 대부분의 경우 여러 함수의 곱으로 되어있어 이를 전부 만족하는 PDF를 구하는 건 힘들지만, 그 중 하나라도 잘 맞는 PDF를 구하기만 해도 충분히 유의미하다.

IS는 실무에서 가장 많이 사용하는 변수 줄이기 기법 중 하나이다. 왜냐면 가장 적용하기도 쉽고, 좋은 분포를 사용하면 매우 효과적이기 때문이다.

6.1. 다중 중요도 표집

결국 렌더링 방정식의 피적분 함수에는 BSDF 항도 있고, 코사인 항도 있고, 들어오는 radiance에 대한 항도 있기 때문에, 얘네를 전부 만족하는 PDF는 찾기도 어려울 뿐더러, 이중 하나만 만족하는 걸 썻다간 결과가 잘 안 나올 수도 있다.

이걸 해결하려는 것이 바로 다중 중요도 표집multiple importance sampling(MIS)이다. 적분을 추정할 때, 여러 분포로부터 표본을 뽑고, 이 중 최소한 하나는(그게 어떤 표본인지 모른다 하더라도) 피적분 함수에 잘 알맞겠거니하는 것이다. MIS에서는 각 분포에 대한 표본마다 가중치를 부여하여 표집 분포와 적분값이 잘 안 맞아서 발생할 수 있는 큰 분산을 없애주는 방법을 제공한다.

만약 ∫f(x)g(x)dx를 추정하기 위해 두 표집 분포 p_f와 p_g를 사용한다고 가정하면, MIS에 의한 추정량은 다음과 같다:

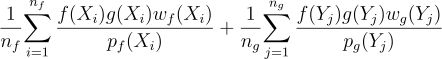
n_f는 p_f 분포에서 뽑은 표본의 수, n_g는 p_g에서 뽑은 표본의 수고, w_f이랑 w_g는 이 추정량의 기대값이 f(x)g(x)의 적분값과 같아지도록 만드는 특수한 가중치 함수이다.

가중치 함수는 표본 X_i나 Y_j가 생성될 수 있는 모든 방법을 고려하는 것이다. 특정 방법을 고려하는 것이 아니다! 대표적인 좋은 가중치 함수로는 균형 휴리스틱balance heuristic이 있다:

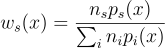
실무에서는 보통 제곱 휴리스틱power heuristic을 사용하여 더욱 분산을 줄이곤 한다. 지수 β에 대하여 표현한다:

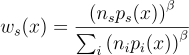
Veach에 의하면 경험적으로 β = 2일 때 제일 잘 된다고 한다.

7. 실험

f(x) = cos(π x / 2) + 2 이고, p가 항등 분포일 때:

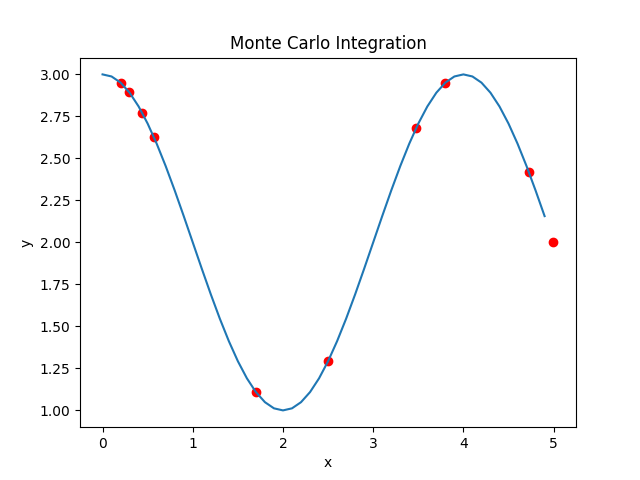
Integral: 10.6366
Uniform Distribution: 11.841182631234615

Latex

p_{i} = \frac{\Phi_{i}}{\sum_{j}{\Phi_{j}}}

\frac{b - a}{N}f{\left(x_{i} \right )}

F_{N} = \frac{b - a}{N}\sum^{N}_{i=1}{f{\left(x_{i} \right )}}

E \left [ F_{N} \right ]  = E\left[ \frac{b - a}{N}\sum^{N}_{i=1}{f{\left(x_{i} \right )}} \right ]\\
= \frac{b - a}{N}\sum^{N}_{i=1}{E\left[f{\left(x_{i} \right )}\right ]} \\
= \frac{b - a}{N}\sum^{N}_{i=1}{\int^{b}_{a}{f{\left(x \right )}p{\left(x \right )}dx}} \\
= \frac{b - a}{N}\sum^{N}_{i=1}{\int^{b}_{a}{f{\left(x \right )}\frac{1}{b - a}dx}} \\
= \frac{1}{N}\sum^{N}_{i=1}{\int^{b}_{a}{f{\left(x \right )}dx}} \\
= \int^{b}_{a}{f{\left(x \right )}dx}

F_{N} = \frac{1}{N}\sum^{N}_{i=1}{\frac{f{\left(x_{i} \right )}}{p{\left(x_{i} \right )}}}

\int^{x_{1}}_{x_{0}}{\int^{y_{1}}_{y_{0}}{\int^{z_{1}}_{z_{0}}{f{\left(x, y, z \right )}}dz}dy}dx

{
    \frac
    {
        {\left(x_{1} - x_{0} \right )}
        {\left(y_{1} - y_{0} \right )}
        {\left(z_{1} - z_{0} \right )}
    }
    {N}
}
{
    \sum_{i}
    {
        f
        {
            \left(X_{i} \right )
        }
    }
}

P{\left(x \right )} = \int^{x}_{0}{p{\left(x' \right )}}dx'

p_{y}{\left(y \right )}{\frac{\textrm{d}y}{\textrm{d}x}} = p_{x}{\left(x \right )}

p_{y}{\left(y \right )} = {\left(\frac{\textrm{d}y}{\textrm{d}x} \right )}^{-1}p_{x}{\left(x \right )}

p_{y}{\left(y \right )} = {\left|\frac{\textrm{d}y}{\textrm{d}x} \right |}^{-1}p_{x}{\left(x \right )}

p_{y}{\left(y \right )} = {\left|\frac{\textrm{d}y}{\textrm{d}x} \right |}^{-1}p_{x}{\left(x \right )}\\
= {\left|\cos{x} \right |}^{-1}p_{x}{\left(x \right )}\\
= \frac{p_{x}{\left(x \right )}}{\left|\cos{x} \right |}\\
= \frac{2x}{\cos{x}}\\
= \frac{2 \arcsin{y}}{\sqrt{1 - y^{2}}}

p_{y}{\left(y \right )} = p_{y}{\left(T{\left(x \right )} \right )} = \frac{p_{x}{\left(x \right )}}{\left | J_{T}{\left(x \right )} \right |}

J_{T} = \begin{pmatrix}
\frac{\delta x}{\delta r} & \frac{\delta x}{\delta \theta}\\ 
\frac{\delta y}{\delta r} & \frac{\delta y}{\delta \theta}
\end{pmatrix}
= \begin{pmatrix}
\cos{\theta} & -r\sin{\theta}\\ 
\sin{\theta} & r\cos{\theta}
\end{pmatrix}

p{\left(x \right )} = \int{p{\left(x, y \right )}}\textrm{d}y

p{\left(y | x \right )} = \frac{p{\left(x, y \right )}}{p{\left(x \right )}}

p{\left(\theta \right )} = \int^{2\pi}_{0}{p{\left(\theta, \phi \right )}\textrm{d}\phi} = \int^{2\pi}_{0}{\frac{\sin{\theta}}{2\pi}\textrm{d}\phi}=\sin{\theta}

p{\left(\phi | \theta\right)} = \frac{p{\left(\theta, \phi \right )}}{p{\left(\theta \right )}}=\frac{1}{2\pi}

P{\left(\theta \right )} = \int^{\theta}_{0}{\sin{\theta'}}\textrm{d}\theta' = 1 - \cos{\theta}\\
P{\left(\phi | \theta\right )} = \int^{\phi}_{0}{\frac{1}{2\pi}}\textrm{d}\phi' = \frac{\phi}{2\pi}

x = \sin {\theta} \cos{\phi} = \cos{\left(2\pi\zeta_{2} \right )}\sqrt{1 - \zeta^{2}_{1}}\\
y = \sin {\theta} \sin{\phi} = \sin{\left(2\pi\zeta_{2} \right )}\sqrt{1 - \zeta^{2}_{1}}\\
z = \cos{\theta} = \zeta_{1}

\int_{H^{2}}{p{\left(\omega \right )}}\textrm{d}\omega = 1\\
\int^{2\pi}_{0}{\int^{\frac{\pi}{2}}_{0}{c \cos{\theta}\sin{\theta}}\textrm{d}\theta}\textrm{d}\phi = 1\\
c 2\pi\int^{\frac{\pi}{2}}_{0}{\cos{\theta}\sin{\theta}}\textrm{d}\theta = 1\\
c = \frac{1}{\pi}

p{\left(\theta, \phi \right )} = \frac{1}{\pi}\cos{\theta}\sin{\theta}

r = \sqrt{\zeta_{1}}\\
\theta = 2\pi\zeta_{2}

\epsilon {\left [ F \right ]} = \frac{1}{V{\left[F \right ]}T{\left[F \right ]}}

\frac{1}{n_{f}}{\sum^{n_{f}}_{i=1}{\frac{f{\left(X_i \right )}g{\left(X_i \right )}w_{f}{\left(X_i\right)}}{p_{f}{\left(X_i \right )}}}} + \frac{1}{n_{g}}{\sum^{n_{g}}_{j=1}{\frac{f{\left(Y_j \right )}g{\left(Y_j \right )}w_{g}{\left(Y_j\right)}}{p_{g}{\left(Y_j \right )}}}}

w_{s}{\left(x \right )} = \frac{n_{s}p_{s}{\left(x \right )}}{\sum_{i}{n_{i}p_{i}{\left(x \right )}}}

w_{s}{\left(x \right )} = \frac{\left( n_{s}p_{s}{\left(x \right )}\right )^{\beta}}{\sum_{i}{\left(n_{i}p_{i}{\left(x \right )} \right )^{\beta}}}