전역 조명을 위한 중요도 재표집 (2022.10.14)

Eurographics 렌더링 심포지엄 (2005)
Kavita Bala, Philip Dutré (편집자)

Justin F. Talbot, Brigham Young University
David Cline, Brigham Young University
Parris Egbert, Brigham Young University

초록

중요도 재표집을 몬테 카를로 적분법의 분산 줄이는 방법으로 사용할 것이다. 중요도 재표집이란 중요도 표집을 할 때 좀 더 동등하게 가중치를 부여한 표본을 뽑는데 사용될 수 있는 표본 생성 방법이다. 이러면 분산이 10~70% 정도로 상당히 줄어들게 된다.

1. 도입

보통 전역 조명은 카지야의 렌더링 방정식을 사용한다. 근데 이 방정식의 적분항은 해석학적으로 풀 수가 없어서 몬테 카를로 적분법으로 그 값을 근사하게 된다. 근데 이게 확률론적인 방법이다 보니까 렌더링한 이미지에 분산에 따른 노이즈가 발생한다. 이걸 처리하려고 여러 분산 줄이기 방법을 사용하는데, 가장 대표적인 방법 중 하나가 중요도 표집이다.

중요도 재표집은 CDF 역방법, 리젝션 방법, 메트로폴리스 표집 등과는 달리 원하는 PDF에 근사하여 분포된 표본을 생성하게 된다. 즉, 무편향성을 유지하려면 추가적인 처리가 필요하다. 중요도 재표집을 통해 중요도 표집에 필요한 표본을 생성하게 되면 재표집한 중요도 표집Resampled Importance Sampling(RIS)이라는 분산 줄이기 기법이 등장한다.

2. 배경

CDF 역방법
리젝션 표집
메트로폴리스 표집
중요도 재표집

이 논문에서 보이려는 것은 전역 조명에서의 중요도 표집을 일반화하는 것이다. Veach가 개발한 MIS의 경우 잘 배치한 가중치를 통해 여러 분포에서 표집이 가능케 된다.

3. 중요도 재표집

중요도 재표집은 컴퓨팅 통계학 분야에서 복잡한 분포로부터 표본을 생성해낼 때 일반적으로 사용하는 방법이다.

Rubin에 의해 1987년에 처음 등장한 개념이다.

우리가 어떤 PDF g로부터 표본을 생성하고 싶은데, g가 해석학적으로 닫힌 구조가 아니거나 적분하거나 역함수를 구하기에 매우 복잡해서 직접적으로(CDF 역방법 등) 처리하기가 불가능하다고 하자. 이럴 경우, 어떤 source 분포 p로부터 여러 표본들을 뽑은 다음, 각 표본마다 적절하게 가중치를 부여한 다음, 이 가중치에 비례한 확률로 한 표본을 재표집resample하면 된다.

중요도 재표집

source 분포 p로부터 M 개(M ≥ 1)의 표본 X = <X₁, … , X_M> 생성

각 표본의 가중치 w_j를 계산

가중치 <w₁, …, w_M>에 비례한 확률로 X로부터 한 표본 Y를 뽑음

이때 가중치를 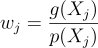Weight 라는 함수로 두고 Y라는 표본을 뽑는다면, 이 Y는 g에 근사한 분포를 띨 것이다. 간단히 말하면 source 분포 p에서 표본을 뽑고, 여기서 한 번 “필터링”을 거쳐서 새로 Y를 뽑는데, 이때 Y가 g에 근사하여 분포하도록 필터링을 해주는 것이다.

이때 M의 값은 일종의 분포 보간 변수로 생각할 수 있다. M = 1이라는 것은 사실상 Y가 p에 대한 분포를 가진다는 뜻이고, M → ∞이면 Y의 분포가 g에 다가갈 것이다. 이때 M의 개수는 유한하므로 M 개를 통한 근사에 의해 발생하는 편향을 줄이려면 충분히 큰 M 값을 사용해야한다.

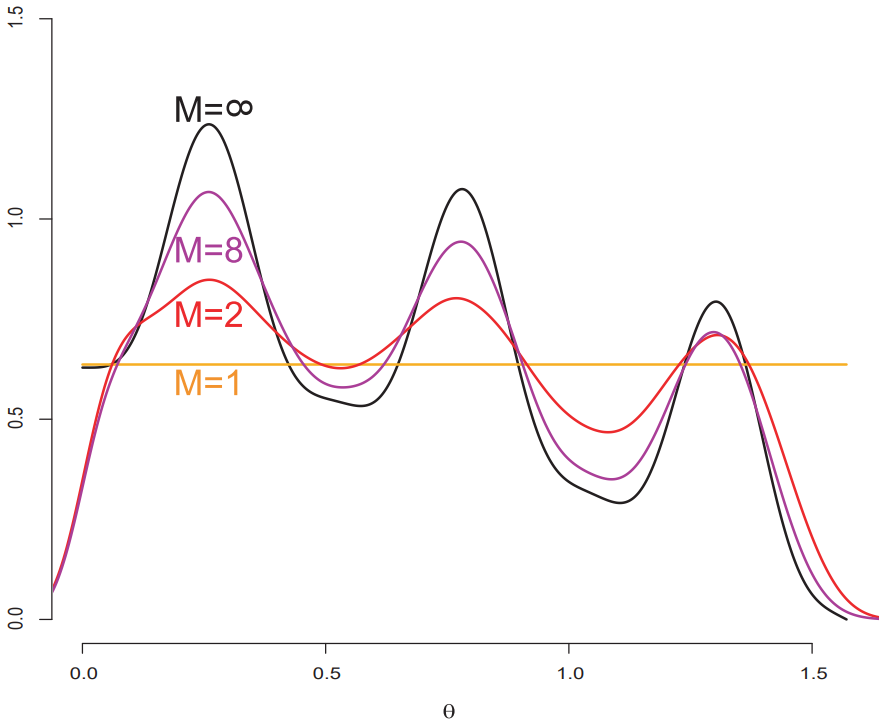
위의 그림의 경우 여러 M 값들에 대해 p가 항등 분포이고, g ∝ cos(θ) + sin⁴(6θ)일 때 Y의 분포를 나타낸 그림이다.

4. RIS

중요도 재표집과 중요도 표집을 합쳐서 나온 분산 줄이기 기법이 바로 재표집된 중요도 표집Resampled Importance Sampling(RIS)이다.

예를 들어 어떤 함수 f(x)의 적분값 I를 구하려고 한다고 가정해보자:

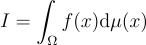
IntegralIOfFunctionF

이때 우리에겐 당장 표집을 할 수 있으나 f를 잘 근사하지는 못하는 source PDF p와 f를 잘 근사하지만 정규화가 되어있지 않거나 표집하기 어려운 sampling PDF g, 두 PDF가 있다고 가정하자. 원래 중요도 표집의 경우엔 p 하나 밖에 못 쓰지만, 이걸 일반화하여 g를 추가하여 추정을 더 잘 할 수 있도록 할 수 있다. RIS는 g에 근사하여 표본을 뽑는 중요도 재표집을 사용하여 g를 무편향적으로 사용할 수 있다.

중요도 재표집 과정에서 표본 집합 X로부터 얻은 Y가 주어졌다면, RIS 추정량을 일종의 가중치 중요도 표집의 형태로 정리할 수 있다:

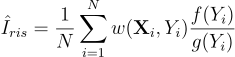
RisInWeightedImportanceSamplingForm

이때 가중치 함수 w는 g가 정규화 되어있지 않다는 점, 그리고 Y가 g에만 근사한다는 점을 고려하여 선택해야 한다. 이에 적합한 w는 놀랍게도 매우 간단한데, 그냥 재표집 단계에서 얻은 가중치들의 평균이다:

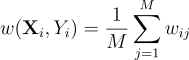
WeightingFunctionW

위의 두 방정식을 합치면 RIS 추정량을 얻게 된다:

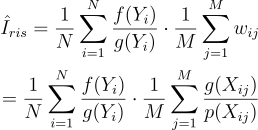
RisEstimator

M = 1이 되면 그냥 일반 중요도 표집이 될 것이다.

RIS 추정량이 무편향이려면 두 가지 조건을 만족해야한다:

g와 p는 f가 0이 아닐 때 반드시 양수여야 한다.
M과 N은 반드시 양수여야 한다.

Latex

Weight

w_{j} = \frac{g{\left(X_{j} \right )}}{p{\left(X_{j} \right )}}

IntegralIOfFunctionF

I = \int_{\Omega}{f{\left(x \right )}\textrm{d}\mu{\left(x \right )}}

RisInWeightedImportanceSamplingForm

\hat{I}_{ris} = \frac{1}{N}\sum^{N}_{i=1}{w{\left(\textbf{X}_{i}, Y_{i} \right )}\frac{f{\left(Y_{i} \right )}}{g{\left(Y_{i} \right )}}}

WeightingFunctionW

w{\left(\textbf{X}_{i}, Y_{i} \right )} = \frac{1}{M}\sum^{M}_{j=1}{w_{ij}}

RisEstimator

\hat{I}_{ris} = \frac{1}{N}\sum^{N}_{i=1}{\frac{f{\left(Y_{i} \right )}}{g{\left(Y_{i} \right )}}\cdot {\frac{1}{M}\sum^{M}_{j=1}{w_{ij}}}}\\
= \frac{1}{N}\sum^{N}_{i=1}{\frac{f{\left(Y_{i} \right )}}{g{\left(Y_{i} \right )}}\cdot {\frac{1}{M}\sum^{M}_{j=1}{\frac{g{\left(X_{ij} \right )}}{p{\left(X_{ij} \right )}}}}}\\