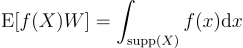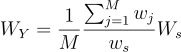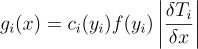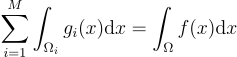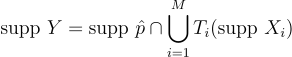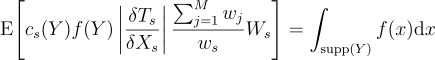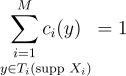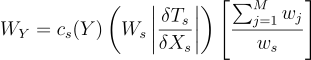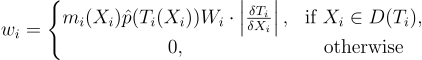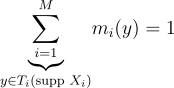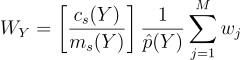일반 재표집 중요도 표집: ReSTIR의 근간 (2022.10.22)
- Daqi Lin, University of Utah.
- Markus Kettunen, NVIDIA.
- Benedikt Bitterli, NVIDIA.
- Jacop Pantaleoni, NVIDIA.
- Cem Yuksel, University of Utah.
- Chris Wyman, NVIDIA
초록
장면들이 너무 복잡해지니깐 실시간으로 광선 추적 / 경로 표집할 때 적은 표본으로 최고의 퀄리티를 뽑아야하는 기술이 더욱 중요해짐… 최근엔 재표집resampling 기반의 RIS로 최대한 뭔가를 해보려고 했는데, 그 중 하나가 시공간으로 복잡한 광전달을 픽셀 당 겨우 몇 개의 표본으로 표집하려는 거였음(ReSTIR). 근데 이게 여러 가정을 하는데, 대표적인게 표본 독립성임. 근데 표본을 재사용하면 상관관계가 발생함. 그러니까 ReSTIR식 반복은 RIS가 이론적으로 제공하는 수렴 보장성을 잃게됨.
그렇기에 이론을 확장한 일반 재표집 중요도 표집(GRIS)을 소개함. 이를 통해 상관관계가 있는, PDF도 모르고 여러 영역에서 나온 표본들에 대해 RIS를 적용할 수 있도록 해줌. 이를 통해 이론적인 배경을 탄탄하게 해서 ReSTIR 기반 표집에서 분산의 유계와 수렴 조건을 제시함. 또한 좀 더 실용적인 알고리듬 설계와 복잡한 shift 매핑을 통해 고급진 픽셀 간 재사용을 가능케 해줌.
여기선 복잡한 장면에서 interactive하게 돌아가는 ReSTIR PT라는 경로 추적 표집기를 소개함. 이 표집기는 다중 튕김 난/정반사 빛을 표집하면서도 픽셀 당 딱 하나의 경로만을 사용함.
1. 도입
요즘 렌더링의 핵심은 몬테 카를로 알고리듬임. 요즘 RTX 덕분에 실시간에 쓸 수 있음. 근데 게임에서 쓰기엔 비용이 좀 빡셈. 최대 픽셀 당 경로 하나 정도?
결국 표본이 적단 소리인데, 이때 분산을 줄이려고 쓴 방법이 중요도 표집임. 근데 빛이 복잡해지면 좋은 표본을 뽑기가 좀 빡세, 아니 사실상 불가능해짐.
그래서 RIS에 기반한 여러 알고리듬들이 나온 것임. 대충 후보를 뽑아 놓고, 얘네들 중에서 다시 또 뽑아서(재표집) 이상적인 분포에 다가가겠다는 소리임. 이상적으로는 충분히 재사용을 하면 “완벽한” 중요도 분포로 수렴을 할 것임. 이걸 저장소 기반으로 시공간 중요도 재표집을 한 ReSTIR 알고리듬을 직접광, 전역 조명, 부피 산란 등에 적용했음. ReSTIR는 스트리밍 알고리듬으로 GPU의 평행성을 사용해서 오류를 줄임.
근데 이런 확률 분포의 수렴을 제대로 다룬 적이 없음. 원본 ReSTIR 논문에선 이 확률 분포가 무편향적이라는 건 보이긴 했는데 모든 상황에서 수렴한다는 점을 증명하지는 않았음.
사실상 제일 핵심은 ReSTIR가 엄청 중요한 부분을 무시한다는 점임: RIS는 독립 항등 분포independent and identically distributed(i.i.d.) 표본을 가정함. 이때 이 표본들은 주로 하나의 source 분포에서 나옴. 재사용을 하게 되면 이 독립성을 위반하게 되고, 하나의 분포에서 나왔다는 점을 무시함. 이러면 수렴이 느려지거나 오히려 벗어나게 됨. 기존 연구에서는 경험적으로 봐씅ㄹ 때 충분히 상관관계가 작으면 수렴에 영향을 주지 않는다고는 했지만, 그래서 상관관계를 줄이는 노력(예를 들어 재사용할 공간 이웃을 확률적으로 뽑기 등)이 실제로 얼마나 수렴을 부장하는지에 대한 부분은 명확하지 않음. 복잡한 광원을 재표집할 땐 이론적 이해 없이는 충분히 상관관계를 줄이는게 불가능할 수도 있음.
이 논문에서는 일반 재표집된 중요도 표집generalized resampled importance sampling (GRIS)이라는 i.i.d. 가정을 처리하면서 ReSTIR와 같이 복잡한 표집기에서의 수렴을 이해하고, 설계하고, 논의하는데 도움이 되는 새로운 이론적 토대를 소개함. GRIS를 통해 서로 다른 영역에서 왔을 수도 있어 하나의 적분으로 추정할 수 있도록 매핑한, 상관관계가 있는 후보 표본을 합쳐서 재표집할 수 있게 해줌.
RIS나 ReSTIR는 GRIS의 한 특수한 경우임.
Contributions:
- Shift 매핑을 통해 다른 픽셀의 경로에 대한 RIS 도출
- 무편향성과 수렴에 대한 조건 제시
- 수렴 제한사항을 만족하면서 분산을 최소화하는 MIS 가중치 도출
- 기존 ReSTIR 설계의 여러 선택들(M-캐핑 등)이 수렴을 보장하는데 얼마나 핵심인지를 알려줌.
- 제대로 shift 매핑을 하면 시공간적으로 경로 재사용할 때 노이즈를 제어할 수 있음을 보임
- BSDF 로브에 특정되도록 연결하여 성능과 퀄리티를 높인 shift 매핑 설계
- GRIS 이론을 통해 경로를 재사용할 수 있는 ReSTIR PT 도출
특히 함수 f를 적분할 때 수렴을 보장하려면 반드시:
- 표본 재사용 때 올바른 MIS 가중치를 사용해야 함
- f/
 이 엄청 커지지 않도록 하는 target 함수
이 엄청 커지지 않도록 하는 target 함수  를 선택해야 함
를 선택해야 함 - 표본의 재표집 가중치 wi이 Var[∑wi] → 0이 되도록 제어함
- f의 영역에 충분히 많은 표본 수가 있도록 보장함
- 특히, 충분한 “표준canonical” 표본이 있도록 함
- 시간 재사용할 때 합리적인 M-캡을 통해 프레임 간의 상관관계에 제한을 두어야 함
새로운 이론과 shift 매핑을 통해 표본을 좀 더 효율적으로 재사용하여 더 강력하면서 무편향적인 광전달 알고리듬을 만들어 복잡한 조명 환경을 처리하면서도 효율적인 GPU 병렬화와 실시간에 적합하도록 함.
1.1. 논문 로드맵
- 2절: GRIS의 핵심 배경(+상당히 유사한 재표집/표집 재사용 알고리듬)을 다룸.
- 3절: RIS 이론의 연구 현황 리뷰 및 확장 필요성을 다룸.
- 4절: 다중 입력 영역 Ωi를 목표 영역 Ω로, 마치 기울기 영역 렌더링에서처럼 shift 맵 Ti: Ωi → Ω를 활용하여 재표집해주어 RIS를 일반화해줌. 영역 Ω에서 임의의 함수 f가 GRIS로 무편향하게 적분하는 조건을 제시하고, 출력 표본 분포가 특정 목표 재표집 PDF
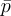
- 5절: 적분 오류가 곧 RIS 정규화 facor의 분산과 직접적으로 유관함을 보임. 이 분산이 사라지면 GRIS는 0 분산 적분이 됨. 이건 현재, 표준canonical 픽셀(이웃 뿐만 아니라)로부터 추가적인 표본을 받고, 강력한 재표집 MIS 가중치를 통해 도달할 수 있음.
- 6절: ReSTIR가 GRIS 수렴 제한사항을 만족하도록하면, 이게 비마르코프 연쇄가 되어 픽셀 당 단일 표본일 때 평생 경로 공간을 탐색하게 됨. 정적인 장면에서는 프레임을 평균하면 수렴하고, 실시간 사용은 각 프레임의 연쇄의 단일 상태를 주게 됨. averaging frames converges, and real-time usage gives a single state of the chain each frame.
- 7절: 픽셀 간 경로 재사용을 위한 shift 매핑을 설계하고, 효율성을 개선하기 위한 몇 가지 새로운 shift 수정사항을 제시함.
- 8절: ReSTIR PT 구현을 다룸.
- 9절: 결과 및 실험 검증을 보임.
2. 배경
요즘 그래픽스 연구의 핵심은 표집, 중요도 표집, 표본 재사용임.
표 1: 표기법 정리
| 변수 | 내용 |
|---|---|
| x, y | 함수의 일반적인 입력 |
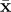 , xi , xi |
경로와 경로 위의 한 점 |
| Ωi | 표본이 그려진 영역 |
| Ω | 함수 f의 적분 영역 |
| Xi | RIS의 입력 표본. 보통 수열임 (Xi)i=1M |
| Y | RIS로 선택한 표본 Y. (가장 단순한 경우 Y = Xs, 일반적인 경우 Y = Ts(Xs)) |
| M, N | RIS의 입력 표본 수와 출력 표본 수 |
| pX(·) | 어떤 위치의 확률 변수 X의 확률 밀도 |
| p(·) | 확률 변수가 명확한 경우에서 위를 간단하게 표기한 것 |
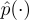 |
정규화하지 않은 목표 분포 (목표: Y ∝  가 되도록 하기) 가 되도록 하기) |
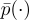 |
정규화 목표 PDF (즉, 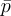 = =  / || / || ||) ||) |
| f(·) | 적분할 함수 (예시. path contribution 함수) |
| gi(·) | Ω의 영역에서 f를 적분할 때 Xi ∈ Ωi가 기여하는 정도를 의미하는 contribution function |
| Wi | 무편향 contribution 가중치; PDF의 역수를 추정함 |
| wi | 재표집 가중치; RIS는 wi/∑wj에 따라 한 Xi를 선택함 |
| ci | contribution MIS 가중치; 기존 연구들의 MIS 가중치 |
| mi | 이 논문의 새로운 재표집 MIS 가중치 |
| Ti(·) | shift 매핑; 표본을 영역 Ωi에서 Ω으로 매핑해줌 |
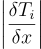 |
매핑 Ti의 야코비 행렬식 |
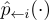 |
“i에서 온  ”. ”.  가 Ωi로의 shift 맵을 포함하도록 일반화함 가 Ωi로의 shift 맵을 포함하도록 일반화함 |
| C | 수렴 증명할 때 유계로 쓰일 여러 상수들 |
| R, |R| | 표준canonical 표본과 그 숫자 |
2.1. 재표집 알고리듬
이 논문은 sampling importance resampling(SIR)에 기반한 재표집 방법을 일반화함. SIR은 독립항등표본의 한 집합 (Xi)i=1M에서 재표집 가중치 wi =  (Xi)/p(Xi)에 비례하여 한 번 더 표집을 한, 좀 더 잘 분포된 표본 (Yi)i=1N을 얻는 과정임. 이때
(Xi)/p(Xi)에 비례하여 한 번 더 표집을 한, 좀 더 잘 분포된 표본 (Yi)i=1N을 얻는 과정임. 이때  (x)은 원하는 (아마 정규화되있지 않은) 목표 분포임. M이 커질 수록 표본 Yi의 분포는
(x)은 원하는 (아마 정규화되있지 않은) 목표 분포임. M이 커질 수록 표본 Yi의 분포는 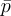 =
=  / ||
/ || ||에 수렴함.
||에 수렴함.
RIS
몬테 카를로 방법에서 SIR을 썻을 때 좀 더 제대로 정규화를 해주는 방법을 제시함.
저장소 표집RS
단일 패스 스트림에서 입력 집합 (Xi)i=1M가 들어왔을 때 무작위로 한 표본을 뽑음. 저장소는 선택한 표본, 현재 스트림의 길이 M, 가중치 wi의 총합을 저장함. 새롭게 스트림에 Xi가 들어오면, 선택한 표본을 확률 wi / ∑j≤iwj에 따라 교체함.
ReSTIR
연쇄된 저장소 재표집으로 픽셀과 프레임 간의 표본을 공유함.
Shift 매핑
ReSTIR이나 RIS도 마찬가지지만, 경로의 표본은 반드시 같은(공유된) 영역에서 와야 함. 그렇기에 서로 다른 영역에서 적분하는 경우를 처리해야함. 이 경우 서로 다른 영역에서의 경로를 매핑해줘야하는 shift 매핑 방법으로 해결함.
3. RIS 리뷰
| RIS 알고리듬 | Talbot et al. 2005 항등 분포 표본 |
Talbot 2005 서로 다르게 분포된 표본 |
GRIS 상관관계 & 서로 다른 source 영역 |
|---|---|---|---|
| (1) M 개의 후보 표본 (X1, …, XM) 생성 | 같은 영역에서 표집: 같은 PDF p, Xi ∈ Ω | 같은 영역에서의 표본: 다른 PDF p, Xi ∈ Ω | 임의의 영역에서의 표본: 다루기 힘든intractable PDF pi도 ㄱㅊ, Xi ∈ Ωi |
| (2) 무편향 contribution 가중치 Wi 구하기 | Wi = 1/p(Xi) | Wi = 1/pi(Xi) | Wi는 반드시 1/pi(Xi)를 무편향적이게 추정해야함 |
| (3) 재표집 가중치 wi 구하기 | 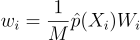 |
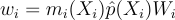 |
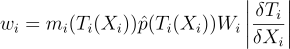 |
| (4) wi에 비례하여 s를 선택하여 영역 Ω에 있는 출력 Y 선택 | 단순히 Y = Xs | 단순히 Y = Xs | Ωi에서 Ω로 매핑된 출력 표본 Y = Ts(Xs) |
3.1. 항등 분포 표본
기본적인 RIS에서는 어떤 영역 Ω로부터 이미 알고 있는 PDF p에서 뽑은 연속된 표본 (Xi)i=1M이 독립항등분포(i.i.d.)를 이루는 경우를 입력으로 받음. 어쨋든 목표는 이 연속된 표본에서 어떤 확률에 따라 Y를 뽑는데, 이 확률이 이루는 분포, 즉 PDF pY가 영역 Ω에서 f를 적분할 때 좀 더 나은 중요도 표집기가 되도록 해주는 것임.
좀 더 구체적으로 설명하자면, 음수가 아닌 목표 함수  를 정의하고, Y를 뽑을 때, 입력 표본의 개수 M이 증가할 수록 구해진 PDF pY가 정규화된
를 정의하고, Y를 뽑을 때, 입력 표본의 개수 M이 증가할 수록 구해진 PDF pY가 정규화된  를 좀 더 잘 근사하도록 해주는 것임. 즉, pY가
를 좀 더 잘 근사하도록 해주는 것임. 즉, pY가 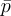 =
=  / ||
/ || ||를 근사하는 것임.
||를 근사하는 것임.
알고리듬적으로 보자면 입력 표본 Xi에서 한 표본 Y = Xs를 확률 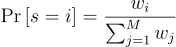 에 따라서 뽑는 것임. 이때 wi는 재표집 가중치임. 이전 연구에서는 wi를
에 따라서 뽑는 것임. 이때 wi는 재표집 가중치임. 이전 연구에서는 wi를  (Xi)/p(Xi)로 두었었음. 여기서 가중치는 상대적인 값임. 즉, 가중치에 어떤 값을 곱하더라도 선택할 확률에는 영향이 없을 것이라는 뜻임:
(Xi)/p(Xi)로 두었었음. 여기서 가중치는 상대적인 값임. 즉, 가중치에 어떤 값을 곱하더라도 선택할 확률에는 영향이 없을 것이라는 뜻임:
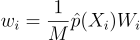
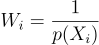
(1)
즉, 위와 같이 표기적 일관성을 위해 표기할 수 있음. 선택한 표본 Y의 PDF 자체는 다루기 힘들더라도, 그 Y의 무편향 contribution 가중치
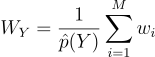
(2)
를 1/pY(Y) 대신 사용할 수 있을 것임. f > 0일 때 pY > 0일 것이라 가정한다면, 즉 f ⊂ supp Y일 때,
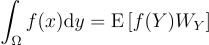
(3)
적절한 조건 하에서는 pY가 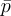 에 수렴하며, 몬테 카를로 분산 Var[f(Y)WY]는 점근적으로 Y가 정확하게
에 수렴하며, 몬테 카를로 분산 Var[f(Y)WY]는 점근적으로 Y가 정확하게 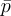 의 분포를 가질 때의 분산에 근사함.
의 분포를 가질 때의 분산에 근사함. 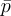 를 f에 비례하도록 선택해야 추정량 f(Y)WY가 점근적으로 분산이 0이 됨을 보장할 수 있음.
를 f에 비례하도록 선택해야 추정량 f(Y)WY가 점근적으로 분산이 0이 됨을 보장할 수 있음.
3.2. 서로 다르게 분포된 표본
만약 표본 Xi가 서로 다른 PDF pi를 갖는다면, 더 복잡해짐. 이러면 재표집 MISresampling MIS라는게 필요해져서 가중치 mi라는 것을 도입하게 됨. 가중치 mi는 mi ≥ 0이며,  의 지지집합support에 있는 모든 x에 대해서
의 지지집합support에 있는 모든 x에 대해서
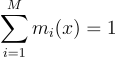
(4)
를 만족함. Talbot은 Veach의 균형 휴리스틱과 유사한 가중치를 제시했음:
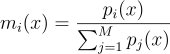
(5)
알고리듬적으로 보면 wi의 1/M 항을 이 MIS 가중치로 변화해주면 됨:
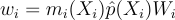
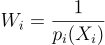
(6)
이때 최소한 한 PDF pi가 각 x ∈ supp  를 커버한다고 하면, 3번 식은 이 새로운 wi를 바탕으로 2번 식의 WY를 갖게 됨. 수렴 조건은 3.1절보다는 더 필요하지만 어쨋든 도달 가능함.
를 커버한다고 하면, 3번 식은 이 새로운 wi를 바탕으로 2번 식의 WY를 갖게 됨. 수렴 조건은 3.1절보다는 더 필요하지만 어쨋든 도달 가능함.
3.3. 왜 재표집을 일반화해야 하는가?
초기에 RIS 쓸 때는 대충 BSDF 중요도 표집할 때나 써서 f에 값싸게 근사하는  를 구해서 여러 값싼 후보들을 생성해서 수렴의 속도를 가속화시키곤 했음.
를 구해서 여러 값싼 후보들을 생성해서 수렴의 속도를 가속화시키곤 했음.
ReSTIR는 픽셀 간의 표본을 재사용해서 여러 적분을 동시다발적으로 추정하는 비용을 줄였음. 이런 목표 아래에선 기존 표본을 재사용하는게 새 표본 만드는 것보다 더 싸다면  가 f보다 간단할 필요가 없음. 게다가 재사용한 표본의 PDF가 목표 피적분함수를 더 잘 근사하면 효율성도 얻음. RIS를 반복적으로 사용하기에
가 f보다 간단할 필요가 없음. 게다가 재사용한 표본의 PDF가 목표 피적분함수를 더 잘 근사하면 효율성도 얻음. RIS를 반복적으로 사용하기에  = f을 써도, 특히 경로가 복잡할 수록 나름 합리적인 선택임.
= f을 써도, 특히 경로가 복잡할 수록 나름 합리적인 선택임.
Talbot의 RIS 이론은 공유된 영역 Ω에서 독립적인 표본 Xi를 가정하는데, ReSTIR는 이 가정을 확대해버렸기 때문에 수렴을 한다는 이론적인 보장이 하나도 없음. 사실 알고리듬 자체에도 뭔가 문제가 안 될 것처럼 보이는 수정사항들을 주었는데, 이 때문에 상관관계에 있는 재사용이 잘못된 결과로의 수렴을 야기할 수도 있음.
4. 일반 RIS
이 논문의 일반 RIS(GRIS)는 서로 다른 영역의 표본을 매핑할 수 있게 해주고, 무편향성과 수렴 조건들이 무엇인지 명시해줌.
전통적인 RIS에서는 한 영역에서 독립된 표본을 뽑았다면, 이 논문에서는 서로 다른 영역 Ωi에서 온, 서로 상관관계가 있을 수도 있는 입력 (Xi)i=1M도 가능함. GRIS는 여기서 표본 Xs를 선택하고, 이걸 shift 매핑 Y = Ts(Xs)을 통해 f의 영역 Ω로 매핑해줌. 이러면 Y의 PDF는 목표 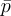 (즉, 정규화된
(즉, 정규화된  )에 다가감.
)에 다가감.
4.1. 개요
결국 입력 표본 Xi가 서로 다른 영역 Ωi에서 올 것이고, 서로 독립적이지 않을 수도 있으며, 적분할 때 1/pi(Xi)을 대체할 무편향 contribution 가중치 Wi ∈ R와 짝을 짓게 될 것임. 이러면 전에 재표집한 입력이 가능해짐. 재표집한 입력 Xi의 PDF pi가 쉽게 다룰 수 있는 함수가 아니더라도, 그 가중치 Wi는 쉽게 다룰 수 있음(2번 식).
영역 Ω에 대해서 f를 적분하도록 표본을 재사용하려면 우선 표본 Xs ∈ Ωs들을 shift 매핑 Ts: Ωs → Ω으로 Ω로 매핑해줘야함. 이러면 PDF를 PDF 변환 규칙에 따라 수정해주기에 shift 맵의 야코비 행렬식 |δTi/δx|를 구해야함.
알고리듬적으로 보자면 이러면 RIS의 여러 측면이 수정됨. 우선 표본을 공통된 영역 Ω로 변환 시켜 줘야하니 재표집 가중치에는 shift 맵 Ti와 그 행렬식이 추가 되어야 함:
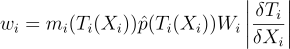
(7)
여기서 pi가 굳이 다루기 쉬울 필요는 없음. 그냥 Wi = 1/pi(Xi) 쓰면 됨. 물론, 수치적 contribution 가중치 Wi를 써도 됨. 이때 이 수치적 contribution 가중치는 예를 들면 직전 RIS 단계에서 가져올 수도 있음(2번 식). 이제 선택한 표본을 적분할 때(혹은 더 재표집할 때) 쓰기 전에 반드시 적절한 영역으로 shift를 해줘야 하므로, 출력 표본은 Y = Ts(Xs)가 됨.
출력 Y의 무편향 contribution 가중치 WY는 2번 식으로 얻을 수 있음. 이때 제약 조건은 다음과 같음: Var[f(Y)WY]가 Var[f(Y)/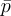 (Y)]에 점근한다고 보장할 수 있을 때, pY가
(Y)]에 점근한다고 보장할 수 있을 때, pY가 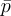 에 수렴해야 함. 이러면
에 수렴해야 함. 이러면  ∝ f일 때 한 개의 Y에 대해서 분산이 0인 적분으로 점근할 수 있음.
∝ f일 때 한 개의 Y에 대해서 분산이 0인 적분으로 점근할 수 있음.
4.2. GRIS를 통한 무편향 적분
우선 영역 Ω에 대해서 함수 f에 대한 무편향 적분을 도출할 것임. 이때 임의의 재표집 가중치 wi를 사용한다고 가정할 것임.
다음과 같이 무편향 contribution 가중치 Wi을 정의할 수 있음:
정의 4.1.
확률 변수 X ∈ Ω에 대한 무편향 contribution 가중치 W ∈ R는 모든 적분 가능한 함수 f : Ω → R에 대하여 아래를 만족하는 임의의 실수 확률 변수 W이다:
(8)
f(X)W은 몬테 카를로 적분의 f(X)/p(X)를 일반화한 것임. 만약 p가 다루기 쉬운 값이라면 W = 1/p(X)를 쓰면 됨. 만약 다루기 쉽지 않다면 RIS로 X를 뽑듯이 가중치를 갖고 무편향 적분을 해줄 수 있음. 적분은 자연스레 p > 0인 곳으로 한정됨. 즉, supp(X)임.
무편향 contribution 가중치는 자연스럽게 주변부 PDF의 역수를 대체하게 됨. 사실, 이 주변부 PDF 역수를 무편향하게 추정하게 됨.
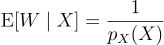
(9)
우연이 아니라, 걍 같은 거임. 주변부 PDF의 역수의 모든 무편향 추정량(9번 식)은 무편향 contribution 가중치(8번 식)이 되며, 그 반대도 성립함.
RIS에서는 wi에 비례하여 Xi를 재표집해주었음. 이렇게 선택한 표본 Xs이 f의 적분의 무편향 추정량을 가져다 주도록 하는 contribution을 표현해주어야 함. 이러려면 우선 각 표본 Xi에 자신의 contribution을 의미하는, 대응하는 기여도 함수contribution function gi : Ωi → R를 지정해주고, s = i번 인덱스를 갖는 표본을 선택했을 때 이 함수의 값을 구해줘야 함.
우선 gs(Xs)Ws를 RIS로 s번 인덱스를 선택할 확률로 나눈 것의 기대값을 확인해봄. i번 인덱스를 선택할 PMF(확률질량함수)는 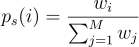 가 됨. 이때 몇 가지만 주의하면:
가 됨. 이때 몇 가지만 주의하면:
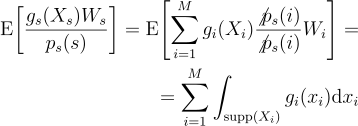
(10)
첫단계에서는 기대값을 가능한 경우들의 합으로 확장을 한 것이고, 두번째 단계에서는 무편향 기여 가중치의 정의를 활용하여 기대값의 합을 적분의 합으로 변환시켜준 것임. RIS는 자연스레 확률 변수의 PDF 값이 0인 영역은 무시할 것이므로 적분을 Xi의 지지집합으로 제한해줌. 이 결과에 따라 남은 적분의 합을 원하는 f의 적분으로 변환해줄 수 있음. 이를 위해선 gi를 잘 선택해주면 됨.
우항이 f의 적분으로 되도록 gi를 고르게 되면 선택 표본 Y = Xs의 무편향 기여도를 구할 수 있게 됨. Xi가 전부 같은 영역 Ω와 같은 지지집합 S에서 왔으며, 이 S에서 모든 wi가 양수라는 특수한 경우에서는 모든 i에 대하여 gi = (1/M) f으로 두어 기본 RIS를 구할 수 있음:
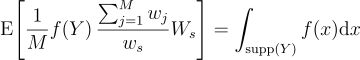
(11)
8번 식과 비교해보면 이 특수한 경우에서의 기대값은 E[f(Y)WY]을 띠는데, 이때
(12)
으로 두었을 것임. 즉, WY는 Y의 무편향 기여도 가중치가 됨. 즉, E[f(Y)WY]는 Y의 지지집합에 대하여 임의의 함수 f를 적분한 값임.
Degenerate의 경우
만약 모든 wi가 0이라면 아무런 표본도 선택할 수 없으며, 기여도는 0이 됨. 직관적으로 보면 기여도가 0인 null 표본 Y∅를 표집 및 적분 영역 밖에서 갖고 온다고 생각할 수 있음(즉,  (Y∅) = f(Y∅) = 0). WY∅의 값은 이러면 의미가 없어지므로 0으로 둘 수 있음.
(Y∅) = f(Y∅) = 0). WY∅의 값은 이러면 의미가 없어지므로 0으로 둘 수 있음.
4.3. Shift 매핑
GRIS에서는 표본 Xi가 임의의 영역 Ωi에서 올 수도 있으므로 이 표본 Xi ∈ Ωi에 대하여 함수 f : Ω → R을 적분하려면 10번 식의 우항을 함수 f의 적분으로 변환해줘야 함. 이러면 Xi를 Ωi에서 Ω로 매핑해주어 결과에서 f를 쓸 수 있게 해주도록 gi를 골라줘야함.
Ωi에서 Ω로 매핑해준다는 것은 적분 변수가 변한다는 것을 의미하므로 반드시 전단사 함수여야함. 복잡한 영역 간의 매핑은 구하기 어려우므로 Ωi의 부분집합을, Ω 안에 있는 Ωi의 부분집합의 이미지로의 전단사 함수를 사용함. 기존 연구에 따르면 이런 전단사 함수를 shift 매핑shift mapping Ti라 부르며, 각 영역 Ωi당 하나가 존재함.
정의 4.2.
영역 Ωi에서 Ω로의 shift 매핑 Ti는 부분집합 D(Ti) ⊂ Ωi에서 부분집합의 이미지 I(Ti) ⊂ Ω로의 전단사 함수임.
직관적으로 보면 다음과 같은 기여도 함수를 골라야할 것임:
(13)
여기서 yi는 Ti(x)를 의미하고, ci : Ω → R은 기여도 MIS 가중치로, y ∈ Ω일 때 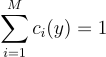 의 임의의 분할을 의미하고,
의 임의의 분할을 의미하고, 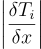 는 x ↦ yi의 야코비 행렬식을 의미함. 원칙상으로 보면
는 x ↦ yi의 야코비 행렬식을 의미함. 원칙상으로 보면
(14)
가 되지만, 세부사항을 놓치면 안됨. 예를 들어 13번 식은 x ∉ D(Ti)에 대해서 정의 되어있지 않기 때문임. 이 경우 x ∉ D(Ti)일 때 gi(x) = 0으로 정의하고, 기여도 MIS를 갱신하여 이를 보상해줌.
여기서 가중치 wi를 목표 함수  와 유관한 임의의 음수가 아닌 확률 변수로 가정함: wi > 0 iff Xi ∈ D(Ti) 이고
와 유관한 임의의 음수가 아닌 확률 변수로 가정함: wi > 0 iff Xi ∈ D(Ti) 이고  (Yi) > 0. 그러므로 Yi = Ti(Xi)가 존재하고
(Yi) > 0. 그러므로 Yi = Ti(Xi)가 존재하고  의 지지집합에 있을 때 필수적으로 wi > 0이어야 함. 아닐 경우 Xi를 고르는 경우를 방지하기 위해 wi = 0으로 둠. 나중엔 이 조건을 조금 완화시켜줄 것임.
의 지지집합에 있을 때 필수적으로 wi > 0이어야 함. 아닐 경우 Xi를 고르는 경우를 방지하기 위해 wi = 0으로 둠. 나중엔 이 조건을 조금 완화시켜줄 것임.
이 가정 하에 보면 각 가능한 Y는 반드시 supp  에 있어야 하며, 양의 PDF를 갖는 하나 이상의 Xi(즉, Xi ∈ supp Xi)에 의해 Y = Ti(Xi)으로 표집 가능해야 하며, 그 반대의 경우도 성립해야함. 수학적으로 표현하자면:
에 있어야 하며, 양의 PDF를 갖는 하나 이상의 Xi(즉, Xi ∈ supp Xi)에 의해 Y = Ti(Xi)으로 표집 가능해야 하며, 그 반대의 경우도 성립해야함. 수학적으로 표현하자면:
(15)
즉, supp Y ⊂ supp  이라는 의미이기도 함. 나중에 supp
이라는 의미이기도 함. 나중에 supp  ⊂ supp Y라고 가정을 할텐데, 이 경우 supp Y = supp
⊂ supp Y라고 가정을 할텐데, 이 경우 supp Y = supp  임을 의미함.
임을 의미함.
10번 식의 좌항에 위의 gi를 x ∉ D(Ti)일 경우 gi(x) = 0라는 조건을 추가하여 넣어주면, 다음과 같은 등식을 얻을 수 있음:
(16)
여기서 Ws는 Xs의 무편향 기여도 가중치임.
이걸 만족하기 위해서는 모든 y ∈ supp Y에 대해서 기여도 MIS 가중치 ci는 다음 조건을 만족해야 함:
(17)
이를 해석하자면, 여러 Ωi에서 왔을 수도 있는 모든 실현 가능한 y는 반드시 총 한 번만 처리가 되어야 함이라는 뜻임. 위의 시그마 연산은 오로지 y가 PDF가 0이 아닐 때 y = Ti(xi)가 될 수 있는 경우에 대해서 영역 Ωi에 대해서만 처리하겠다는 것임. 원칙상 음수값인 ci도 작동은 하겠지만, 나중에 다루겠지만 ci ≥ 0이어야만 GRIS를 여러 단계로 연쇄할 수 있음.
16번 식의 기대값은 영역 Ω에 대해서 적분 가능한 임의의 함수 f E[f(Y)WY]의 형태를 띠고, 우항은 8번 식의 무편향 기여도 가중치의 정의에 따라 f가 Y의 지지집합에 대해서 적분을 하는 것임. 그러므로:
(18)
WY가 1/pY(Y)의 무편향적인 추정량일 때, f(Y)WY는 Y의 지지집합에 대하여 f를 적분한 값을 무편향적으로 추정함.
즉, 이를 통해 언제 GRIS가 임의의 함수 f를 적분할 수 있는지를 알 수 있음: 확률 변수 Xi의 지지집합(Ti로 Ω로 매핑한 것)이 f의 지지집합을 같이 커버할 때임.
이 조건은 하나의 표집 영역을, 예를 들어 Ω1을 f의 영역으로 고르고 항등 shift T1(x) = x을 Ω1에 적용하고, 피적분함수 f를 위해 설계한 중요도 표집기에서 X1을 생성하면 자연스럽게 만족이 됨(즉, f(x1) > 0일 때마다 p(x1) > 0가 되도록). 이런 표본을 표준canonical이라고 부름. pX1가 뭔지 알고 있으니 무편향 기여도 가중치 W1 = 1/pX1(X1)을 쓰면 됨.
나중에 보이겠지만, ReSTIR 표집기들은 귀납적으로 이 사실에 기반하여 생성할 수 있음.
제한 조건 완화하기
Yi = Ti(Xi)에 대해서  (Yi) > 0일 때 wi > 0이어야 한다는 조건은 ci(Yi) = 0이거나 Wi일 때, 즉 기대값이 변하지 않을 때 wi = 0가 될 수 있도록 해주어 완화시킬 수 있음. 17번 식의 유효성이 supp
(Yi) > 0일 때 wi > 0이어야 한다는 조건은 ci(Yi) = 0이거나 Wi일 때, 즉 기대값이 변하지 않을 때 wi = 0가 될 수 있도록 해주어 완화시킬 수 있음. 17번 식의 유효성이 supp  ∩ ∪iTi(supp Xi)에서 반드시 명시적으로 보장되어야 15번 식이 가능해짐.
∩ ∪iTi(supp Xi)에서 반드시 명시적으로 보장되어야 15번 식이 가능해짐.
4.4. 점근 완전 중요도 표집
GRIS의 목표는 Talbot의 RIS처럼 원하는 분포를 따르는 표본을 표집하는 것임. 출력 표본 Y의 주변부 확률 분포 pY가 입력 표본 수가 무한대로 발산할 때 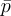 에 수렴해야함.
에 수렴해야함.
이는 다음 재표집 가중치를 사용할 경우 만족함:
(19)
위에서 mi는 재표집 MIS 가중치이고 Wi는 무편향 기여도 가중치임. wi를 정규화한 것이 재표집 확률이어야 하므로 wi는 반드시 음수가 아니어야 함. 즉, 그러므로 mi와 Wi도 음수가 아니어야 하며, 앞으로는 그렇다고 가정하겠음.
 의 지지집합 밖에서는
의 지지집합 밖에서는  = 0이므로 가중치 wi는 0일 것임. mi의 조건도 ci이랑 비슷함. supp Y의 모든 y에 대해서:
= 0이므로 가중치 wi는 0일 것임. mi의 조건도 ci이랑 비슷함. supp Y의 모든 y에 대해서:
(20)
게다가 mi ≥ 0이어야 함. 여기서 합은 오로지 양의 PDF를 생성하는 y를 생성하는 인덱스들만 고려함. 무편향 적분에서는 mi가 ci에 의해 생성된 합의 일부분을 무효화하지 않도록 ci(y) ≠ 0일 때 mi(y) > 0이어야 함.
19번 식의 wi를 18번 식에 대입하게 되면 새 표본 Y에 대한 무편향 기여도 가중치를 얻을 수 있게 됨:
(21)
ci(y) ≠ 0일 때 mi(y) > 0이어야 한다는 조건에 의해 자연스레 0에 의한 나눗셈 문제를 해결할 수 있음. 이제 mi = ci가 되도록 선택하는 것이 가장 이상적임을 증명하여 다음 조건을 만족하도록 함.
Latex
TalbotResamplingWeightWi
w_{i} = m_{i}{\left(X_{i} \right )}\hat{p}{\left(X_{i} \right )}W_{i}
ResamplingWeightWi
w_{i} = m_{i}{\left(T_{i}{\left(X_{i} \right )} \right )}\hat{p}{\left(T_{i}{\left(X_{i} \right )} \right )}W_{i}\left | \frac{\delta{T_{i}}}{\delta{X_{i}}} \right |
TalbotEtAlUnbiasedContributionWeightWi
W_{i} = \frac{1}{p{\left(X_{i} \right )}}
UnbiasedContributionWeightOfSelectedSampleY
W_{Y} = \frac{1}{\hat{p}{\left(Y \right )}}\sum_{i=1}^{M}{w_{i}}
ExpectedValueOfIntegralF
\int_{\Omega}{f{\left(x \right )}}\textrm{d}y = \textrm{E}\left [ f{\left(Y \right )} W_{Y}\right ]
ResamplingMisWeightsSum
\sum_{i=1}^{M}{m_{i}{\left(x \right )}} = 1
TalbotResamplingMisWeightMi
m_{i}{\left(x \right )} = \frac{p_{i}{\left(x \right )}}{\sum_{j=1}^{M}{p_{j}{\left(x \right )}}}
UnbiasedContributionWeightCondition
\textrm{E}{\left[f{\left(X \right )}W \right ]} = \int_{\textrm{supp}{\left(X \right )}}{f{\left(x \right )}}\textrm{d}x
ReciprocalOfTheMarginalPdf
\textrm{E}{\left[W \mid X \right ]} = \frac{1}{p_{X}{\left(X \right )}}
SelectionPmf
p_{s}{\left(i \right )} = \frac{w_{i}}{\sum_{j=1}^{M}{w_{j}}}
ExpectationOfGsWsDividedByTheRisSelectionProbabilityOfIndexS
\textrm{E}{\left[\frac{g_{s}{\left(X_{s} \right )}W_{s}}{p_{s}{\left(s \right )}} \right ]} = \textrm{E}{\left[\sum_{i=1}^{M}g_{i}{\left(X_{i}\right)}\frac{\not{p_{s}{\left(i \right )}}}{\not{p_{s}{\left(i \right )}}}W_{i} \right ]} = \\
= \sum_{i=1}^{M}{\int_{\textrm{supp}{\left(X_{i} \right )}}{g_{i}{\left(x_{i} \right )}}\textrm{d}x_{i}}
BasicRisRecovery
\textrm{E}{\left[ \frac{1}{M}f{\left(Y \right )\frac{\sum_{j=1}^{M}{w_{j}}}{w_{s}}W_{s}} \right ]}
= \int_{\textrm{supp}{\left(Y \right )}}{f{\left(x \right )}}\textrm{d}x
UnbiasedContributionWeightForBasicRis
W_{Y} = \frac{1}{M}\frac{\sum_{j=1}^{M}{w_{j}}}{w_{s}}W_{s}
IntuitiveShiftMappingContributionFunction
g_{i}{\left(x \right )} = c_{i}{\left(y_{i} \right )}f{\left(y_{i} \right )}\left | \frac{\delta{T_{i}}}{\delta{x}} \right |
Unity
\sum_{i=1}^{M}{c_{i}{\left(y \right )}} = 1
InPrinciple
\sum_{i=1}^{M}{\int_{\Omega_{i}}{g_{i}{\left(x \right )}\textrm{d}x}} = \int_{\Omega}{f{\left(x \right )}}\textrm{d}x
ShiftMappingAssumptions
\textrm{supp }{Y} = \textrm{supp }{\hat{p}} \cap \bigcup_{i=1}^{M}{T_{i}{\left(\textrm{supp }{X_{i}} \right )}}
ShiftMappingEquality
\textrm{E}{\left[c_{s}{\left(Y \right )}f{\left(Y \right )}\left | \frac{\delta{T_{s}}}{\delta{X_{s}}} \right |\frac{\sum_{j=1}^{M}{w_{j}}}{w_{s}}W_{s} \right ]}
= \int_{\textrm{supp}{\left(Y \right )}}{f{\left(x \right )}}\textrm{d}x
ConstraintOfContributionMisWeightsCi
\underset{y \in T_{i}{\left(\textrm{supp }{X_{i}} \right )}}{\sum_{i=1}^{M}{c_{i}{\left(y \right )}}} = 1
UnbiasedContributionWeightWy
W_{Y} = c_{s}{\left(Y\right)}\left(W_{s}\left | \frac{\delta{T_{s}}}{\delta{X_{s}}} \right |\right)\left [ \frac{\sum_{j=1}^{M}{w_{j}}}{w_{s}} \right ]
ResamplingWeights
w_{i} = \left\{\begin{matrix}
m_{i}{\left(X_{i} \right )}\hat{p}{\left(T_{i}{\left(X_{i} \right )} \right )}W_{i}\cdot\left | \frac{\delta{T_{i}}}{\delta{X_{i}}} \right |, & \textrm{if } X_{i} \in D{\left(T_{i} \right )},\\ 0, & \textrm{otherwise}
\end{matrix}\right.
RequirementsForMi
\underset{y \in T_{i}{\left(\textrm{supp }{X_{i}} \right )}}{\underbrace{\sum_{i=1}^{M}}}{m_{i}{\left(y \right )}} = 1
UnbiasedContributionWeight
W_{Y} = \left [ \frac{c_{s}{\left(Y\right)}}{m_{s}{\left(Y \right )}} \right ] \frac{1}{\hat{p}{\left(Y \right )}}\sum_{j=1}^{M}{w_{j}}