실무에서의 ReSTIR (2022.09.17)

Home

공부 노트

논문들

2020년에 SIGGRAPH에 나온 Spatiotemporal reservoir resampling for real-time ray tracing with dynamic direct lighting 논문으로부터 ReSTIR 붐이 시작되었는데, 해당 기술을 적용한 여러 논문을 읽고 정리해본 노트다.

참고한 논문들:

초록

공통적인 문제:

도입

배경지식

렌더링 방정식

어떤 점 y에서 직접광에 의해 ω 방향으로 반사되는 radiance L은 광원의 표면 A에 대한 적분식으로 다음과 같이 구할 수 있음:

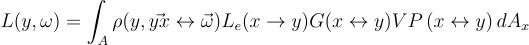
RenderingEquation

여기서 ρ는 BSDF, Le는 광원이 내뿜는 radiance, V는 x와 y 사이의 상호 가시성, G는 역 제곱 거리와 코사인 항을 갖는 기하적 요소.

Importance Sampling (IS)

이때 위의 식을 x에 대해 간략하게 표현한다면:

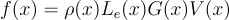
ImportanceSamplingFx

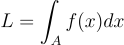
ImportanceSamplingL

이걸 몬테 카를로 Importance Sampling(IS)를 통해 source 확률밀도함수 p(xi)에서 N 개의 샘플 xi 고르면 적분식을 estimate 할 수 있게 됨:

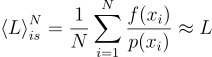
ImportanceSamplingMonteCarloIntegration

이때 f(x)가 0이 아닐 때 p(x)가 양수이기만 하면 무편향성을 띰. 또한 이상적으로는 p(x)가 f(x)와 상관관계가 있으면 분산이 낮아짐.

다중 Importance Sampling (MIS)

실제로는 f(x)에 비례하여 샘플링하는 건 불가능. 특히나 V(x) 항 때문에 더더욱 문제임. 근데 적분식의 강 항(BSDF, Le 등)에 대하여 샘플링하는 건 ㄱㅊ임.

즉, M 개의 샘플링 방법 ps이 존재할 때, 각 s번째 샘플링 방법마다 Ns 개의 샘플을 뽑고, 이들을 하나로 합쳐서 하나의 가중치가 부여된 estimator로 만들어 줄 수 있음. 이것이 바로 MIS:

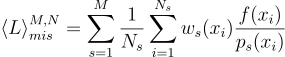
MultipleImportanceSamplingMonteCarloIntegration

이때 가중치 ws 들의 합이 1만 이루기만 하면 MIS는 무편향성을 가짐. 대표적인 가중치 함수로는 balance heuristic 함수를 쓺:

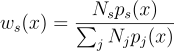
MultipleImportanceSamplingBalanceHeuristic

Resampled Importance Sampling (RIS)

MIS가 각 항의 선형 결합으로부터 샘플링을 했다면, RIS는 이 항들의 곱에 근사approximately하게 비례하여 샘플링을 해주는 것임.

근데 애초에 IS를 이유는, 당연히 아래의 식과 같이 완벽한 source PDF를 구할 수 있다면 아무런 문제가 되지 않을 것임:

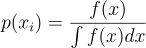
ResampledImportanceSamplingOptimalSourcePdf

근데 애초에 우리가 몬테 카를로를 하는 이유 자체가 적분을 못해서인데, 여기서 저 적분을 구하라고 하는게 말이 안되잖음.

그래서 몬테 카를로는, “알아서 pdf p 잘 구하시구요, 그걸 이 방법으로 하면 대충 estimation 가능해요~”라는 거고, IS는 “pdf p가 f에 비례하면 좀 더 좋아요~”라는 것이고, MIS는 “f에 비례하는 p 구하기 어려우시죠? 꼼수로 선형 결합을 드리겠습니다~”라는 것이다.

위의 식처럼 p를 구하면 완벽한 IS가 될 것이지만, 그러려면 애초의 적분이 필요하니까…

근데 완벽한 p를 구한다는 발상을 반대로 생각해서, 애초에 완벽한 p를 근사를 해보려고 시도할 수도 있다. 즉, 저 적분을 한 번 근사해보자는 것이다.

즉, 현실적으로 f에 대해서 샘플링하기가 힘드니까, 일단 f를 샘플링의 대상이 아니라, 우리가 구할 target 함수 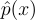ResampledImportanceSamplingDesiredPdf로 다르게 바라보자는 것이다. (이때 이 target 함수는 PDF처럼 normalized 된 상태가 아닐 것이다!)

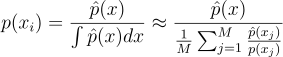
ResampledImportanceSamplingNormalizationApproximation

그렇다면 이제 이 target을 근사할 새로운 source PDF p가 생긴다. 즉, 적당히 최적이면서 구하기 쉬운 source 분포 p로부터 한 개 이상(M ≥ 1)의 후보 샘플들(x = {x1, …, xM})을 우선 뽑는 것이다. 이제 여기서 임의의 z 번째 샘플 하나를 다음 이산 확률로 뽑는다:

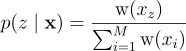
ResampledImportanceSamplingCandidateProbability

이때 가중치 w는 다음과 같다:

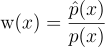
ResampledImportanceSamplingCandidateWeight

이렇게 되면 자연스럽게 구하려는 식을 다시 쓸 수 있게 된다:

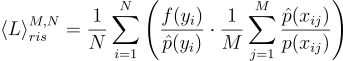
ResampledImportanceSamplingMonteCarloIntegration

여기서 N 개의 샘플이 아니라, 하나의 샘플만을 다루게 된다면 식을 다음과 같이 정리할 수 있다:

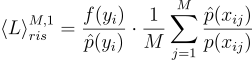
ResampledImportanceSamplingSingleSampleMonteCarloIntegration

이렇게 되면 마치 y 라는 샘플을 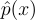ResampledImportanceSamplingDesiredPdf에서 뽑은 것처럼 속여서 사용할 수 있게 된다. 뒤에 있는 괄호 안에 있는 내용은 “아, 이게 보면 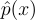ResampledImportanceSamplingDesiredPdf 분포에서 뽑은 것처럼 보이긴 하는데, 사실은 p에서 온거고, 이걸로 근사를 하려고 했던거에요~”라고 알려주는 거다.

RIS는 M, N ≥ 1이고, f가 0이 아닐 때 p와 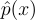ResampledImportanceSamplingDesiredPdf가 양수기만 하면 무편향성을 띤다.

RIS 알고리듬:

void ResampledImportanceSampling(float& outSample, float& outWeightSum, size_t numCandidates, const Pixel& pixel)
{
  float* samples = reinterpret_cast<float*>(::malloc(numCandidates * sizeof(float)));
  float* weights = reinterpret_cast<float*>(::malloc(numCandidates * sizeof(float)));
  ::memset(samples, 0, numCandidates * sizeof(float));
  ::memset(weights, 0, numCandidates * sizeof(float));
  float weightSum = 0.0f;

  for (size_t i = 0; i < numCandidates; ++i)
  {
    samples[i] = GenerateSample(SourcePdf);
    weights[i] = TargetPdf(samples[i]) / SourcePdf(samples[i]);
    weightSum += weights[i];
  }

  // Select from candidates w
  // Compute normalized CDF C from weights
  // draw random index z ∈ [0, M) using C to sample ∝ w_z
  size_t z = GenerateSample(C);

  outSample = samples[z];
  outWeightSum = weightSum;
}

참고문헌

  1. Talbot, Justin and Cline, David and Egbert, Parris. Importance Resampling for Global Illumination. Eurographics Symposium on Rendering (2005).
  2. Efraimidis, Pavlos S. and Spirakis, Paul G. Weighted random sampling with a reservoir. Information Processing Letters, Volume 97, Issue 5, 16 March 2006, Pages 181-185.

Latex

L(y, \omega) = \int_{A}{\rho{ \left ( y, \vec{yx} \leftrightarrow \vec{\omega} \right ) } L_{e}{\left( 
x \rightarrow y \right)} G{\left(x \leftrightarrow y \right )}VP\left(x \leftrightarrow y \right )dA_x}

L = \int_{A}{f{\left(x\right)}dx}

f{\left(x \right )} = \rho{\left(x \right )}L_{e}{\left(x \right )}G{\left(x \right )}V{\left(x \right )}

\left \langle L \right \rangle^{N}_{is} = \frac{1}{N}\sum^{N}_{i=1}{\frac{f{\left(x_{i} \right )}}{p{\left(x_{i} \right )}}}\approx L

\left \langle L \right \rangle^{M, N}_{mis} = \sum^{M}_{s=1}{\frac{1}{N_{s}}\sum^{N_{s}}_{i=1}{w_{s}{\left(x_i\right)}\frac{f{\left(x_{i} \right )}}{p_{s}{\left(x_{i} \right )}}}}

w_{s}{\left(x\right)} = \frac{N_{s}p_{s}{\left(x \right )}}{\sum_{j}{N_{j}p_{j}{\left(x \right )}}}

p{\left(z \mid \textbf{x} \right )} = \frac{\textrm{w}{\left(x_{z} \right )}}{\sum^{M}_{i=1}{\textrm{w}{\left(x_{i} \right )}}}

\textrm{w}{\left(x \right )} = \frac{\hat{p}{\left(x \right )}}{p{\left(x \right )}}

p{\left(x_{i} \right )} = \frac{f{\left(x \right )}}{\int{f{\left(x \right )}dx}}

p{\left(x_{i} \right )} = \frac{\hat{p}{\left(x \right )}}{\int{\hat{p}{\left(x \right )}dx}} \approx
\frac{\hat{p}{\left(x \right )}}{\frac{1}{M}\sum^{M}_{j=1}{\frac{\hat{p}{\left(x_{j} \right )}}{p{\left(x_{j} \right )}}}}

\left \langle L \right \rangle^{M, N}_{ris} = \frac{1}{N}\sum^{N}_{i=1}{\textrm{w}{\left(x_{i}, y_{i}\right)}\frac{f{\left(y_{i} \right )}}{\hat{p}{\left(y_{i} \right )}}}

\textrm{w}{\left(x_{i}, y_{i}\right)} = \frac{1}{M}\sum^{M}_{j=1}{\textrm{w}_{ij}}

\left \langle L \right \rangle^{M, N}_{ris} = \frac{1}{N}\sum^{N}_{i=1}{\left( {\frac{f{\left(y_{i} \right )}}{\hat{p}{\left(y_{i} \right )}}} \cdot {\frac{1}{M}\sum^{M}_{j=1}{\frac{\hat{p}{\left( x_{ij} \right )}}{p{\left(x_{ij} \right )}}}}\right ) }

\left \langle L \right \rangle^{M, 1}_{ris} = {\frac{f{\left(y_{i} \right )}}{\hat{p}{\left(y_{i} \right )}}} \cdot {\frac{1}{M}\sum^{M}_{j=1}{\frac{\hat{p}{\left( x_{ij} \right )}}{p{\left(x_{ij} \right )}}}}

P_{i} = \frac{\textrm{w}{\left(x_{i} \right )}}{\sum^{M}_{j=1}\textrm{w}{\left(x_{j} \right )}}

W{\left(z \right )} = \frac{1}{\hat{p}{\left(z \right )}M}\sum^{M}_{j=1}{\frac{\hat{p}{\left(y_{j} \right )}}{p{\left(y_{i} \right )}}}

\left \langle L \right \rangle^{M, 1}_{ris} = f{\left(y_{i} \right )} W{\left(y_{i} \right )}