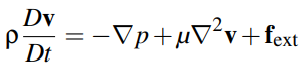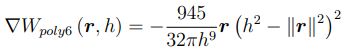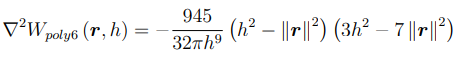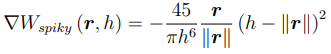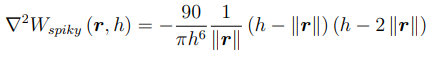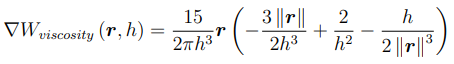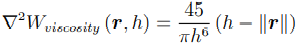Smoothed Particles Hydrodynamics by CUDA (27 NOV 2021)
Smoothed Particle Hydrodynamics
In order to understand the SPH method, we must understand how can we simulate liquid. The idea is that liquid is essentially a group of small molecules, also known as H2O’s. All the microinteractions between these molecules, the “particles” creates the entire physical simulation of the liquid. Thus by approximating a liquid body into a group of particles could simulate the liquid efficiently. This is a particle-based simulation of a liquid.
To understand how a particle-based simulation works, the best way is to see this paiting of Georges-Pierre Seurat, a French neo-impressionist painter famous for his pointillistic paintings.
Each particle is merely an approximation of the light rays coming to our human eyes. The particle-based methods are often classified as a Lagrangian framework—a framework that solves the fluid motion by following the fluid parcel, such as particles.1
History
The SPH method was originally introduced in astrophysics community by Monaghan2 and activelocityy studied in computational fluid dynamics field as well3. Soon after, computer animation started to adopt the idea of SPH4, 5 and also became one of the core frameworks for commercial products like RealFlow6.1
Fundamentals
SPH is an interpolation method for particle systems. This is probably the single most important sentence regarding SPH. This means that SPH is not a specific algorithm on determining the behavior of a liquid body. To understand how we use this interpolation method to simulate liquid particles, we must start from the real basics: physics and mathematics.
Classical Mechanics: Kinematics7
Kinematics is a subfield of physics, develocityoped in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies (groups of objects) without considering the forces that cause them to move.
Before proceeding to the next chapter, I should mandate all the readers to read the velocityocity and speed chapter of the wikipedia page on kinematics. The core concepts to understand are: positionition, velocityocity, acceleration, relative positionition, relative velocityocity, relative acceleration.
Classical Mechanics: Continuum Mechanics8
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles.
Modeling an object as a continuum assumes that the substance of the object completely fills the space it occupies. Modeling objects in this way ignores the fact that matter is made of atoms, and so is not continuous; however, on length scales much greater than that of inter-atomic distances, such models are highly accurate. Fundamental physical laws such as the conservation of mass, the conservation of momentum, and the conservation of energy may be applied to such models to derive differential equations describing the behavior of such objects, and some information about the material under investigation is added through constitutive relations.
Continuum mechanics deals with physical properties of solids and fluids which are independent of any particular coordinate system in which they are observed. These physical properties are then represented by tensors, which are mathematical objects that have the required property of being independent of coordinate system. These tensors can be expressed in coordinate systems for computational convenience.
Momentum9
In Newtonian mechanics, linear momentum, translational momentum, or simply momentum is the product of the mass and velocityocity of an object. It is a vector quantity, positionsessing a magnitude and a direction. If m is an object’s mass and v is its velocityocity (also a vector quantity), then the object’s momentum p is
In the International System of Units (SI), the unit of measurement of momentum is the kilogram metre per second (kg⋅m/s), which is equivalent to the newton-second.
Classical Field Theories: Lagrangian Specificattion of the Flow Field10
From now on, when we talk about Velocities and accelerations, we are talking about the Velocities and accelerations of each particles in a space through time. In the Lagrangian description, the flow is described by a function:
giving the positionition of the particle labeled x0 at time t.
Within a chosen coordinate system, x0 is referred to as the Lagrangian coordinates of the flow.
Further references to help you understand the concept of Lagrangian coordinate system:
Fluid Mechanics: Navier-Stokes Equations11
In physics, the Navier-Stokes equations are certain partial differential equations which describe the motion of viscous fluid substances.
The Navier-Stokes equations mathematically express conservation of momentum and conservation of mass for Newtonian fluids. They are sometimes accompanied by an equation of state relating pressure, temperature and density.12 They arise from applying Isaac Newton’s second law to fluid motion, together with the assumption that the stress in the fluid is the sum of a diffusing viscous term (proportional to the gradient of velocityocity) and a pressure term—hence describing viscous flow.
The Navier–Stokes momentum equation can be derived as a particular form of the Cauchy momentum equation, whose general convective form is:
by setting the Cauchy stress tensor σ to be the sum of a viscosity term τ (the deviatoric stress) and a pressure term −pI (volumetric stress) we arrive at
where
- D/Dt is the material derivative, defined as ∂/∂t + u ⋅ ∇,
- ρ is the density,
- u is the flow velocityocity,
- ∇ ⋅ is the divergence,
- p is the pressure,
- t is time,
- τ is the deviatoric stress tensor, which has order 2,
- g represents body accelerations acting on the continuum, for example gravity, inertial accelerations, electrostatic accelerations, and so on,
The incompressible momentum Navier–Stokes equation results from the following assumptions on the Cauchy stress tensor:13
- the stress is Galilean invariant: it does not depend directly on the flow velocityocity, but only on spatial derivatives of the flow velocityocity. So the stress variable is the tensor gradient ∇u.
- the fluid is assumed to be isotropic, as with gases and simple liquids, and consequently τ is an isotropic tensor; furthermore, since the deviatoric stress tensor can be expressed in terms of the dynamic viscosity μ:
where
is the rate-of-strain tensor. So this decompositionition can be made explicit as:13
Dynamic viscosity μ need not be constant – in incompressible flows it can depend on density and on pressure. Any equation that makes explicit one of these transport coefficient in the conservative variables is called an equation of state.14
The divergence of the deviatoric stress is given by:
because ∇ ⋅ u = 0 for an incompressible fluid.
Incompressibility rules out density and pressure waves like sound or shock waves. The incompressible flow assumption typically holds well with all fluids at low Mach numbers (say up to about Mach 0.3). The incompressible Navier–Stokes equations are best visualised by dividing for the density:
- ν is the kinematic viscosity
It is well worth observing the meaning of each term (compare to the Cauchy momentum equation):
The higher-order term, namely the shear stress divergence ∇ ⋅ τ, has simply reduced to the vector Laplacian term μ∇2u.[13] This Laplacian term can be interpreted as the difference between the velocityocity at a point and the mean velocityocity in a small surrounding volume. This implies that – for a Newtonian fluid – viscosity operates as a diffusion of momentum, in much the same way as the heat conduction. In fact neglecting the convection term, incompressible Navier–Stokes equations lead to a vector diffusion equation (namely Stokes equations), but in general the convection term is present, so incompressible Navier–Stokes equations belong to the class of convection–diffusion equations.
Let’s now rearrange the equation into a SPH terminology:
In order to calculate the left-side term, then we need to understand each terms in the right-side.
The first term -Δp is the pressure acceleration term.
The second term μ∇2v is the viscosity acceleration term.
The last term is the external body forces.
Conclusion
The basic structure of the algorithm:
- update v by solving Dv/Dt = v∇2v + 1/ρ fext
- determine ∇p by enforcing the continuity equation,
- update v by solving Dv/Dt = -1/ρ ∇p
- update x by solving Dx/Dt = v
where ν = µ/ρ denotes the kinematic viscosity. In this way, the “weaker” forces could be handled using explicit time integration while we can solve for the pressure gradients using a more sophisticated implicit solver in order to keep the simulation robust for large time steps.15
Why SPH?
Now we have a glimpse of theoretical background to simulate fluid. But the problem is that these v’s and p’s are all fundamentally vector and scalar fields. But the only data we currently have is the positionition of each particles in 3d space. Reconstructing a field from discrete points is where we need some form of interpolation. Using discrete points in the neighborhood, we can approximate the vector / scalar field using some form of interpolant. This is where SPH comes in.
SPH Discretization
The concept of SPH can be generally understood as a method for the discretization of spatial field quantities and space differential operators, e.g., gradient, divergence, curl, etc.15
We can deep dive into all the discussions and theories about dirac functions and stuff, but I will go straight to the equations we would use.
If there exists a function A(xi), the function can be discretized into:
The discretization of differential operator would be:
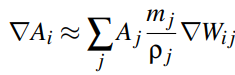
For improved readability, we will drop the second argument of the kernel function and use the abbreviation:
In order to ensure symmetry, the equation is then rearranged into:
The discretization of laplace operator would be:
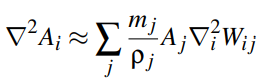
In order to cope with very poor estimate of the 2nd-order differential, Brookshaw propositioned an improved discrete operator for the Laplacian:
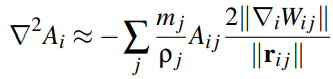
However, the resulting 2nd-order derivatives has problems that in the context of physics simulations, the forces derived using this operator are not conserving momentum. By a little bit of mathematical magic, the formula can be rearranged into:
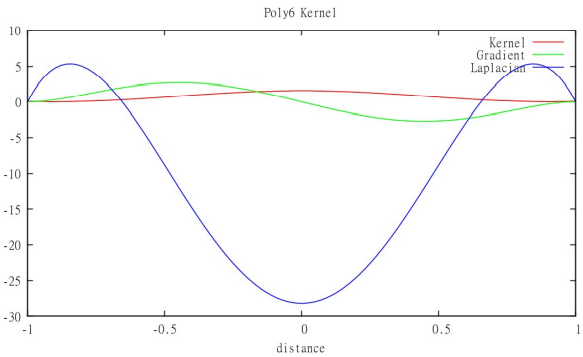
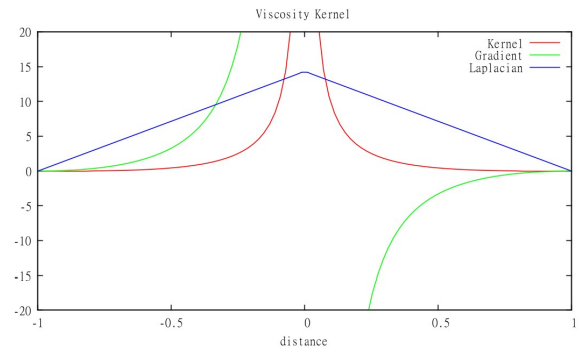
Kernel Functions
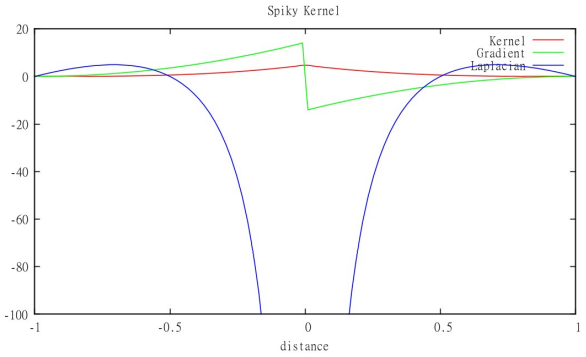
Images and equations from [Staubach. 2010.]16.
- 6th degree polynomial kernel (default kernel)
- Spiky kernel (pressure kernel)
- Viscosity kernel
Mass Density Estimation
Using 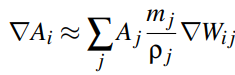, the density field at positionition xi results in:
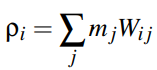
Simple Fluid Simulator15
Let us go back to the basic structure of the algorithm:
- update v by solving Dv/Dt = v∇2v + 1/ρ fext
- determine ∇p by enforcing the continuity equation,
- update v by solving Dv/Dt = -1/ρ ∇p
- update x by solving Dx/Dt = v
Now we can calculate each elements using SPH techniques.
- Viscosity
- External Body Force
- Pressure
- State Equation
Based on the knowledge that we have acquired up to this point, we are now able to implement a simple state-equation based simulator for weakly compressible fluids with operator splitting using SPH and symplectic Euler integration.
Following is a simulation loop for SPH simulation of weakly compressible fluids:
1 for all particle i do
2 Reconstruct density ρi at xi with mass density equation
3 for all particle i do
4 Compute Fiviscosity = miv∇2vi, e.g., using discretization of laplace operator
5 vi* = vi + Δt/mi(Fiviscosity + Fiext)
6 for all particle i do
7 Compute Fipressure = -mi/ρ ∇p using state equation and symmetric formula for discretization of differential operator
8 for all particle i do
9 vi(t + Δt) = vi* + Δt/miFipressure
10 xi(t + Δt) = xi + Δtvi(t + Δt)
Let us break down each components into equations:
- Density ρi
- Viscosity Force
- External Force
- Pressure Force
Neighborhood Search
The propositioned algorithm above has one major flaw: the time complexity is O(n2). However, if we can limit the number of particles to be looped to m, then the time complexity is reduced to O(mn). If the number of m is small enough, then we can expect a linear complexity of O(n).
Based on the particles sample in CUDA SDK Samples, the grid hashing works as following:
// calculate address in grid from positionition (clamping to edges)
__device__ uint CalculateGridHash(int3 Gridpositionition);
// Calculate positionition in uniform grid
__device__ int3 CalculateGridpositionition(float3 positionition);
// Calculate grid hash
void CalculateGridHashes(uint* OutGridParticleHashes, uint* OutGridParticleIndices, float* Positions, uint NumParticles);
// Sort particles based on hash
void SortParticles(uint* OutGridParticleHashes, uint* GridParticleIndices, uint NumParticles);
// Reorder particle arrays into sorted order and
// find start and end of each cell
void ReorderDataAndFindCellStart(uint* OutCellStarts, uint* OutCellEnds, float* OutSortedPositions, float* OutSortedVelocities, uint* GridParticleHashes, uint* GridParticleIndices, float* Positions, float* Velocities, uint NumParticles, uint NumCells);
CalculateGridHash(Gridpositionition)- Simple hashing
Gridpositionition.x = Gridpositionition.x & (gParameters.GridSize.x - 1); // wrap grid, assumes size is power of 2return ((Gridpositionition.z * gParameters.GridSize.y) * gParameters.GridSize.x) + (Gridpositionition.y * gParameters.GridSize.x) + Gridpositionition.x;
CalculateGridpositionition(positionition)- based on the
gParameters.WorldOrigincoordinate andgParameters.CellSizesize, we can calculate the grid coordinate. Gridpositionition.x = floor((Particle.x - gParameters.WorldOrigin.x) / gParameters.CellSize.x);
- based on the
CalculateGridHashes(OutGridParticleHashes, OutGridParticleIndices, Positions, NumParticles)- for each
index,- calculate grid positionition of
Positions[index] - calculate grid hash of the grid positionition
- save the hash value into
OutGridParticleHashes[index] - save the index value into
OutGridParticleIndices[index]
- calculate grid positionition of
- for each
SortParticles(OutGridParticleHashes, GridParticleIndices, NumParticles)- using the
thrustlibrary, sortOutGridParticleHashesbyGridParticleIndices
- using the
ReorderDataAndFindCellStart(uint* OutCellStarts, uint* OutCellEnds, float* OutSortedPositions, float* OutSortedVelocities, uint* GridParticleHashes, uint* GridParticleIndices, float* Positions, float* Velocities, uint NumParticles, uint NumCells)- for each
index- save the hash value
GridParticleHashes[index]into thesharedHasharray in shared memory region - based on the
sharedHashvalue, find the index toOutCellStarts[hash]andOutCellEnds[hash] - based on the sorted index from
GridParticleIndices, sort thePositionsandVelocitiesintoOutSortedPositionsandOutSortedVelocities
- save the hash value
- for each
These functions are all implemented as CUDA functions, and are given from the CUDA SDK Sample.
CUDA Implementation
We must understand some terminologies beforehand. When we refer to as Host, it means that the data resides in the host memory, which is the CPU-side memory: RAM. On the other hand, when we refer to as Device, it means that the data resides in the device memory, which is the GPU-side memory: VRAM. CPU nor GPU can access directly into each other’s memory, and should be access via system bus which requires system calls such as cudaMemcpy.
Common CUDA Types / Global Variables / Functions
// Types
struct <type-name>3 // int3, uint3, float3, double3
{
<type-name> x;
<type-name> y;
<type-name> z;
};
struct <type-name>4 // int4, uint4, float4, double4
{
<type-name> x;
<type-name> y;
<type-name> z;
<type-name> w;
};
// make_int3, make_uint3, make_float3, make_double3
<type-name>3 make_<type-name>3(<type-name> x, <type-name> y, <type-name> z);
// make_int4, make_uint4, make_float4, make_double4
<type-name>4 make_<type-name>4(<type-name> x, <type-name> y, <type-name> z, <type-name> w);
<type-name>4 make_<type-name>4(<type-name>3 vector, <type-name> w);
// CUDA graphics interop resource
struct cudaGraphicsResource;
// Functions
// CUDA Built-in Functions
// Frees memory on the device
cudaError_t cudaFree(void* devPtr)
// Frees page-locked memory
cudaError_t cudaFreeHost(void* ptr);
// Allocate memory on the device
cudaError_t cudaMalloc(void** p, size_t s);
// Allocates page-locked memory on the host
cudaError_t cudaMallocHost(void** ptr, size_t size);
// Copies data between host and device
cudaError_t cudaMemcpy(void* dst, const void* src, size_t count, enum cudaMemcpyKind kind)
// Custom Functions
#define checkCudaErrors(val) check((val), #val, __FILE__, __LINE__)
// compute grid and thread block size for a given number of elements
void ComputeGridSize(uint NumElements, uint BlockSize, uint& OutNumBlocks, uint& OutNumThreads);
void InitializeCuda(GPU_SELECT_MODE Mode, int32 SpecifiedDeviceId);
void ReportGPUMemeoryUsage();
void VerifyCudaError(cudaError err);
// kernel functions
__device__ float Poly6KernelBySquaredDistance(float SquaredDistance);
__device__ float3 Poly6KernelGradient(float3 R);
__device__ float Poly6KernelLaplacianBySquaredDistance(float SquaredDistance);
__device__ float3 SpikyKernelGradient(float3 R);
__device__ float ViscosityKernelLaplacianByDistance(float Distance);
Particle System
The algorithm used is following:
// ParticleSystem.h
// CUDA runtime
#include <cuda_runtime.h>
// CUDA utilities and system includes
#include <helper_functions.h>
#include <helper_cuda.h> // includes cuda.h and cuda_runtime_api.h
class ParticleSystem
{
public:
// methods
...
private:
bool mbInitialized = false;
uint32_t mNumParticles;
// CPU data
float* mHostPositions = nullptr; // Particle Positions
float* mHostVelocities = nullptr; // Particle Velocities
float* mHostNonPressureForces = nullptr; // Particle Non Pressure Forces
float* mHostPressureForces = nullptr; // Particle Pressure Forces
float* mHostDensities = nullptr; // Particle Densities
float* mHostPressures = nullptr; // Particle Pressures
uint32_t* mHostParticleHashes = nullptr;
uint32_t* mHostCellStarts = nullptr;
uint32_t* mHostCellEnds = nullptr;
// GPU data
float* mDevicePositions = nullptr; // CUDA device memory Positions
float* mDeviceVelocities = nullptr;
float* mDeviceNonPressureForces = nullptr;
float* mDevicePressureForces = nullptr;
float* mDeviceDensities = nullptr;
float* mDevicePressures = nullptr;
float* mDeviceSortedPositions = nullptr;
float* mDeviceSortedVelocities = nullptr;
// grid data for sorting method
uint32_t* mDeviceGridParticleHashes = nullptr; // Grid hash value for each particle
uint32_t* mDeviceGridParticleIndices = nullptr; // Particle index for each particle
uint32_t* mDeviceCellStarts = nullptr; // Indices of start of each cell in sorted list
uint32_t* mDeviceCellEnds = nullptr; // Indices of end of cell
// parameters
SimParams mParameters;
uint3 mGridSize;
uint32_t mNumGridCells;
StopWatchInterface* mTimer = nullptr;
...
};
Global Parameters
// ParticlesKernel.cuh
// simulation parameters
struct SimParams
{
// values for grid hashing
uint3 GridSize;
uint NumCells;
float3 WorldOrigin;
float3 CellSize;
float ParticleRadius;
float BoundaryDamping;
// global parameters for sph values
float Mass;
float KernelRadius;
float KernelRadiusSquared;
float GasConst;
float RestDensity;
float Viscosity;
float Threshold;
float ThresholdSquared;
float SurfaceTension;
float3 Gravity;
// constants for kernel functions
float Poly6;
float Poly6Gradient;
float Poly6Laplacian;
float SpikyGradient;
float ViscosityLaplacian;
};
Initialization / Destruction
// ParticleSystem.h
class ParticleSystem
{
public:
ParticleSystem(uint32_t NumParticles, uint3 GridSize, bool bUseOpenGl);
~ParticleSystem();
Initialize();
Destroy();
InitializeGrid();
Reset();
...
};
// ParticleSystem.cpp
ParticleSystem::ParticleSystem(uint32_t NumParticles, uint3 GridSize)
: mNumParticles(NumParticles)
, mGridSize(GridSize)
, mNumGridCells(mGridSize.x * mGridSize.y * mGridSize.z)
{
memset(mParameters, 0, sizeof(SimParams));
mParameters.GridSize = mGridSize;
mParameters.NumCells = mNumGridCells;
mParameters.WorldOrigin = make_float3(-1.0f, -1.0f, -1.0f);
mParameters.ParticleRadius = 1.0f / 64.0f;
mParameters.BoundaryDamping = -0.5f;
// global parameters for sph values
mParameters.Mass = 0.02f;
mParameters.KernelRadius = 2.0f * mParameters.ParticleRadius;
mParameters.KernelRadiusSquared = mParameters.KernelRadius * mParameters.KernelRadius;
mParameters.CellSize = mParameters.KernelRadius;
mParameters.GasConst = 3.0f;
mParameters.RestDensity = 998.29f;
mParameters.Viscosity = 3.5f;
mParameters.Threshold = 7.065f;
mParameters.ThresholdSquared = mParameters.Threshold * mParameters.Threshold;
mParameters.SurfaceTension = 0.0728f;
mParameters.Gravity = make_float3(0.0f, -9.80665f, 0.0f);
// constants for kernel functions
mParameters.Poly6 = 315.0f / (64.0f * CUDART_PI_F * pow(m_params.kernelRadius, 9.f));
mParameters.Poly6Gradient = -(945.0f / (32.f * CUDART_PI_F * pow(m_params.kernelRadius, 9.f)));
mParameters.Poly6Laplacian = -(945.0f / (32.f * CUDART_PI_F * pow(m_params.kernelRadius, 9.f)));
mParameters.SpikyGradient = -(45.0f / (CUDART_PI_F * pow(m_params.kernelRadius, 6.f)));
mParameters.ViscosityLaplacian = 45.0f / (CUDART_PI_F * pow(m_params.kernelRadius, 6.f));
InitializeCuda(SPECIFIED_DEVICE_ID, 0);
}
ParticleSystem::~ParticleSystem()
{
Destroy();
mNumParticles = 0u;
cudaError_t CudaStatus = cudaDeviceReset();
}
void ParticleSystem::Initialize()
{
assert(!mbInitialized);
// allocate host storage
uint32_t MemorySize = sizeof(float) * mNumParticles * 4u;
mHostPositions = reinterpret_cast<float*>(malloc(MemorySize));
mHostVelocities = reinterpret_cast<float*>(malloc(MemorySize));
mHostNonPressureForces = reinterpret_cast<float*>(MemorySize));
mHostPressureForces = reinterpret_cast<float*>(malloc(MemorySize));
mHostDensities = reinterpret_cast<float*>(malloc(sizeof(float) * mNumParticles));
mHostPressures = reinterpret_cast<float*>(malloc(sizeof(float) * mNumParticles));
memset(reinterpret_cast<void*>(mHostPositions), 0, MemorySize);
memset(reinterpret_cast<void*>(mHostVelocities), 0, MemorySize);
memset(reinterpret_cast<void*>(mHostNonPressureForces), 0, MemorySize);
memset(reinterpret_cast<void*>(mHostPressureForces), 0, MemorySize);
memset(reinterpret_cast<void*>(mHostDensities), 0, sizeof(float) * mNumParticles);
memset(reinterpret_cast<void*>(mHostPressures), 0, sizeof(float) * mNumParticles);
mHostCellStarts = malloc(sizeof(uint32_t) * mNumGridCells);
mHostCellEnds = malloc(sizeof(uint32_t) * mNumGridCells);
memset(reinterpret_cast<void*>(mHostCellStarts), 0, sizeof(uint32_t) * mNumGridCells);
memset(reinterpret_cast<void*>(mHostCellEnds), 0, sizeof(uint32_t) * mNumGridCells);
// allocate GPU data
checkCudaErrors(cudaMalloc(reinterpret_cast<void**>(&mDevicePositions), MemorySize));
checkCudaErrors(cudaMalloc(reinterpret_cast<void**>(&mDeviceVelocities), MemorySize));
checkCudaErrors(cudaMalloc(reinterpret_cast<void**>(&mDeviceNonPressureForces), MemorySize));
checkCudaErrors(cudaMalloc(reinterpret_cast<void**>(&mDevicePressureForces), MemorySize));
checkCudaErrors(cudaMalloc(reinterpret_cast<void**>(&mDeviceDensities), sizeof(float) * NumParticles));
checkCudaErrors(cudaMalloc(reinterpret_cast<void**>(&mDevicePressures), sizeof(float) * NumParticles));
checkCudaErrors(cudaMalloc(reinterpret_cast<void**>(&mDeviceSortedPositions), MemorySize));
checkCudaErrors(cudaMalloc(reinterpret_cast<void**>(&mDeviceSortedVelocities), MemorySize));
checkCudaErrors(cudaMalloc(reinterpret_cast<void**>(&mDeviceGridParticleHashes), sizeof(uint) * mNumParticles));
checkCudaErrors(cudaMalloc(reinterpret_cast<void**>(&mDeviceGridParticleIndice), sizeof(uint) * mNumParticles));
checkCudaErrors(cudaMalloc(reinterpret_cast<void**>(&mDeviceCellStarts), sizeof(uint) * mNumGridCells));
checkCudaErrors(cudaMalloc(reinterpret_cast<void**>(&mDeviceCellEnds), sizeof(uint) * mNumGridCells));
mbInitialized = true;
}
void ParticleSystem::Destroy()
{
assert(mbInitialized);
if (mHostPositions != nullptr)
{
free(mHostPositions);
}
if (mHostVelocities != nullptr)
{
free(mHostVelocities);
}
if (mHostNonPressureForces != nullptr)
{
free(mHostNonPressureForces);
}
if (mHostPressureForces != nullptr)
{
free(mHostPressureForces);
}
if (mHostDensities != nullptr)
{
free(mHostDensities);
}
if (mHostPressures != nullptr)
{
free(mHostPressures);
}
if (mHostCellStarts != nullptr)
{
free(mHostCellStarts);
}
if (mHostCellEnds != nullptr)
{
free(mHostCellEnds);
}
if (mDeviceVelocities != nullptr)
{
cudaFree(mDeviceVelocities);
}
if (mDeviceDensities != nullptr)
{
cudaFree(mDeviceDensities);
}
if (mDeviceNonPressureForces != nullptr)
{
cudaFree(mDeviceNonPressureForces);
}
if (mDevicePressureForces != nullptr)
{
cudaFree(mDevicePressureForces);
}
if (mDevicePressures != nullptr)
{
cudaFree(mDevicePressures);
}
if (mDeviceSortedPositions != nullptr)
{
cudaFree(mDeviceSortedPositions);
}
if (mDeviceSortedVelocities != nullptr)
{
cudaFree(mDeviceSortedVelocities);
}
if (mDeviceGridParticleHashes != nullptr)
{
cudaFree(mDeviceGridParticleHashes);
}
if (mDeviceGridParticleIndice != nullptr)
{
cudaFree(mDeviceGridParticleIndice);
}
if (mDeviceCellStarts != nullptr)
{
cudaFree(mDeviceCellStarts);
}
if (mDeviceCellEnds != nullptr)
{
cudaFree(mDeviceCellEnds);
}
if (mDevicePositions != nullptr)
{
cudaFree(mDevicePositions);
}
mbInitialized = false;
}
void AParticleActor::InitializeGrid(uint32_t Size, float Spacing, float Jitter, uint32_t mNumParticles)
{
srand(1973);
for (uint32_t z = 0u; z < Size[2]; ++z)
{
for (uint32_t y = 0u; y < Size[1]; ++y)
{
for (uint32_t x = 0u; x < Size[0]; ++x)
{
uint32_t i = (z * Size[1] * Size[0]) + (y * Size[0]) + x;
if (i < mNumParticles)
{
mHostPositions[i * 4u + 0u] = (Spacing * x) + mParameters.ParticleRadius - 1.0f + (frand() * 2.0f - 1.0f) * Jitter;
mHostPositions[i * 4u + 1u] = (Spacing * y) + mParameters.ParticleRadius - 1.0f + (frand() * 2.0f - 1.0f) * Jitter;
mHostPositions[i * 4u + 2u] = (Spacing * z) + mParameters.ParticleRadius - 1.0f + (frand() * 2.0f - 1.0f) * Jitter;
mHostPositions[i * 4u + 3u] = 1.0f;
mHostVelocities[i * 4u + 0u] = 0.0f;
mHostVelocities[i * 4u + 1u] = 0.0f;
mHostVelocities[i * 4u + 2u] = 0.0f;
mHostVelocities[i * 4u + 3u] = 0.0f;
}
}
}
}
}
void ParticleSystem::Reset()
{
float Jitter = mParameters.ParticleRadius * 0.01f;
uint32_t Size = static_cast<int32_t>(ceilf(powf(static_cast<float>(mNumParticles), 1.0f / 3.0f)));
InitializeGrid(Size, mParameters.KernelRadius, Jitter, mNumParticles);
cudaMemcpy(mDevicePositions, HostPositions, sizeof(float) * mNumParticles * 4, cudaMemcpyHostToDevice);
cudaMemcpy(mDeviceVelocities, HostVelocities, sizeof(float) * mNumParticles * 4, cudaMemcpyHostToDevice);
cudaMemcpy(mDeviceNonPressureForces, HostForces, sizeof(float) * mNumParticles * 4, cudaMemcpyHostToDevice);
cudaMemcpy(mDevicePressureForces, HostForces, sizeof(float) * mNumParticles * 4, cudaMemcpyHostToDevice);
cudaMemcpy(mDeviceDensities, HostDensities, sizeof(float) * mNumParticles, cudaMemcpyHostToDevice);
cudaMemcpy(mDevicePressures, HostPressures, sizeof(float) * mNumParticles, cudaMemcpyHostToDevice);
}
Update
Remember the simple algorithm we saw?
It is now time to implement the algorithm.
1 for all particle i do
2 Reconstruct density ρi at xi with mass density equation
3 for all particle i do
4 Compute Fiviscosity = miv∇2vi, e.g., using discretization of laplace operator
5 vi* = vi + Δt/mi(Fiviscosity + Fiext)
6 for all particle i do
7 Compute Fipressure = -1/ρ ∇p using state equation and symmetric formula for discretization of differential operator
8 for all particle i do
9 vi(t + Δt) = vi* + Δt/miFipressure
10 xi(t + Δt) = xi + Δtvi(t + Δt)
Before we calculate these values, we must first sort the particles first:
// ParticleSystem.h
class ParticleSystem
{
public:
...
void Update(float DeltaTime);
...
};
// ParticleSystem.cpp
void ParticleSystem::Update(float DeltaTime)
{
assert(mbInitialized);
// update constants
SetParameters(&mParameters);
// calculate grid hash
CalculateGridHashes(mDeviceGridParticlehashes, mDeviceGridParticleIndice, mDevicePositions, mNumParticles);
// sort particles based on hash
SortParticles(mDeviceGridParticleHashes, mDeviceGridParticleIndice, mNumParticles);
// reorder particle arrays into sorted order and
// find start and end of each cell
ReorderDataAndFindCellStart(mDeviceCellStarts,
mDeviceCellEnds,
mDeviceSortedPositions,
mDeviceSortedVelocities,
mDeviceGridParticleHashes,
mDeviceGridParticleIndice,
mDevicePositions,
mDeviceVelocities,
mNumParticles,
mNumGridCells);
}
Densities
void ComputeDensities(float* OutDensities, float* SortedPositions, uint* GridParticleIndice, uint* CellStarts, uint* CellEnds, uint NumParticles, uint NumCells)
{
// thread per particle
uint NumThreads;
uint NumBlocks;
ComputeGridSize(NumParticles, 64u, NumBlocks, numThreads);
// execute the kernel
ComputeDensitiesDevice<<<NumBlocks, NumThreads>>>(OutDensities,
(float4*) SortedPositions,
GridParticleIndice,
CellStarts,
CellEnds,
NumParticles);
// check if kernel invocation generated an error
getLastCudaError("Kernel execution failed");
}
__global__
void ComputeDensitiesDevice(float* OutDensities, // output: new density
float4* SortedPositions, // input: sorted Positions
uint* GridParticleIndice, // input: sorted particle indices
uint* CellStarts,
uint* CellEnds,
uint NumParticles)
{
uint Index = (blockIdx.x * blockDim.x) + threadIdx.x;
if (Index >= NumParticles)
{
return;
}
// read particle data from sorted arrays
float3 positionition = make_float3(SortedPositions[Index].x, SortedPositions[Index].y, SortedPositions[Index].z);
// get address in grid
int3 Gridpositionition = CalculateGridHash(positionition);
// examine neighbouring cells
float Density = 0.0f;
for (int z = -1; z <= 1; ++z)
{
for (int y = -1; y <= 1; ++y)
{
for (int x = -1; x <= 1; ++x)
{
int3 Neighbourpositionition = Gridpositionition + make_int3(x, y, z);
Density += ComputeDensitiesByCell(Neighbourpositionition, Index, positionition, SortedPositions, CellStarts, CellEnds);
}
}
}
// write new velocityocity back to original unsorted location
uint OriginalIndex = GridParticleIndice[Index];
OutDensities[OriginalIndex] = Density;
}
__device__
float ComputeDensitiesByCell(int3 Gridpositionition,
uint Index,
float3 positionition,
float4* SortedPositions,
uint* CellStarts,
uint* CellEnds)
{
uint GridHash = CalculateGridHash(Gridpositionition);
// get start of bucket for this cell
uint StartIndex = CellStarts[GridHash];
float Density = 0.0f;
if (StartIndex != 0xffffffff) // cell is not empty
{
// iterate over particles in this cell
uint EndIndex = CellEnds[GridHash];
for (uint j = StartIndex; j < EndIndex; ++j)
{
float3 Neighborpositionition = make_float3(SortedPositions[j]);
float3 rij = (positionition - Neighborpositionition);
float r2 = LengthSquared(rij);
if (r2 < gParameters.KernelRadiusSquared)
{
// m_j * W_ij
Density += gParameters.Mass * Poly6KernelBySquaredDistance(r2);
}
}
}
return Density;
}
Non Pressure Forces
- Viscosity Force
- External Force
In order to approximate the Laplacian of the velocityocity field we combine an SPH derivative with a finite difference derivative which yields the following equation17:
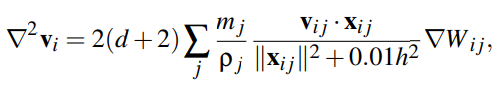
where xij = xi − xj, vij = vi − vj and d is the number of spatial dimensions.
void ComputeNonPressureForces(float* OutNonPressureForces,
float* OutVelocities,
float* SortedPositions,
float* SortedVelocities,
float* Densities,
float* Pressures,
uint* GridParticleIndice,
uint* CellStarts,
uint* CellEnds,
uint NumParticles,
uint NumCells)
{
// thread per particle
uint NumThreads;
uint NumBlocks;
ComputeGridSize(NumParticles, 64u, NumBlocks, NumThreads);
// execute the kernel
ComputeNonPressureForcesDevice<<<NumBlocks, NumThreads>>>((float4*) OutNonPressureForces
(float4*) OutVelocities,
(float4*) SortedPositions,
(float4*) SortedVelocities,
Densities,
Pressures,
DeltaTime,
GridParticleIndice,
CellStarts,
CellEnds,
NumParticles);
// check if kernel invocation generated an error
getLastCudaError("Kernel execution failed");
}
__global__
void ComputeNonPressureForcesDevice(float4* OutNonPressureForces, // output: updated non pressure forces
float4* OutVelocities, // output: updated Velocities
float4* SortedPositions, // input: sorted Positions
float4* SortedVelocities,
float* Densities,
float DeltaTime,
uint* GridParticleIndice, // input: sorted particle indices
uint* CellStarts,
uint* CellEnds,
uint NumParticles)
{
uint Index = (blockIdx.x * blockDim.x) + threadIdx.x;
if (Index >= NumParticles)
{
return;
}
// read particle data from sorted arrays
uint OriginalIndex = GridParticleIndice[Index];
float3 positionition = make_float3(SortedPositions[Index]);
float3 velocityocity = make_float3(SortedVelocities[Index]);
float Density = Densities[OriginalIndex];
// get address in grid
int3 Gridpositionition = CalculateGridpositionisition(positionition);
// examine neighbouring cells
float3 ViscosityForce = make_float3(0.0f);
for (int z = -1; z <= 1; z++)
{
for (int y = -1; y <= 1; y++)
{
for (int x = -1; x <= 1; x++)
{
int3 Neighbourpositionition = Gridpositionition + make_int3(x, y, z);
ComputeNonPressureForcesByCell(Neighbourpositionition,
Index,
ViscosityForce,
positionition,
velocityocity,
Density,
SortedPositions,
SortedVelocities,
Densities,
GridParticleIndice,
CellStarts,
CellEnds);
}
}
}
// viscosityForce = - mass * viscosity_coefficient * sigmas
// viscosityForce = mass * viscosity_coefficient * 2 * (d + 2)
ViscosityForce *= -gParameters.Mass * gParameters.Viscosity * 10.0f;
// externalForce = mass * gravitational acceleration
float3 ExternalForce = gParameters.Mass * gParameters.Gravity;
OutNonPressureForces[OriginalIndex] = ViscosityForce + ExternalForce;
OutVelocities[OriginalIndex] += make_float4((OutNonPressureForce[OriginalIndex] / gParameters.Mass) * DeltaTime, 0.0f);
}
__device__
void ComputeNonPressureForcesByCell(int3 Gridpositionition,
uint Index,
float3& OutViscosityForce,
float3 positionition,
float3 velocityocity,
float Density,
float4* SortedPositions,
float4* SortedVelocities,
float* Densities,
uint* GridParticleIndice,
uint* CellStarts,
uint* CellEnds)
{
uint GridHash = CalculateGridHash(Gridpositionition);
// get start of bucket for this cell
uint StartIndex = CellStarts[GridHash];
if (StartIndex != 0xffffffff) // cell is not empty
{
// iterate over particles in this cell
uint EndIndex = CellEnds[GridHash];
for (uint j = StartIndex; j < EndIndex; j++)
{
if (j != Index) // check not colliding with self
{
float3 Neighborpositionition = make_float3(SortedPositions[j]);
float3 Rij = (positionition - Neighborpositionition);
float R2 = LengthSquared(Rij);
if (R2 < gParameters.KernelRadiusSquared)
{
uint OriginalIndex = GridParticleIndice[j];
float3 Neighborvelocityocity = make_float3(SortedVelocities[j]);
float3 Vij = velocityocity - Neighborvelocityocity;
// sigma (mass_j / density_j) * v_ij * (2 * ||gradient of kernel|| / ||r_ij||)
// sigma (mass_j / density_j) * (v_ij * x_ij) / (||x_ij||^2 + 0.01 * h^2) ∇W_ij
OutViscosityForce += (gParameters.Mass / Densities[OriginalIndex]) * dot(Vij, Rij) / (dot(Rij, Rij) + 0.01f * gParameters.KernelRadiusSquared) * Poly6KernelGradient(Rij);
}
}
}
}
}
Pressure Forces
Compute Fipressure = -1/ρ ∇p using state equation and symmetric formula for discretization of differential operator.
State equations are used to compute pressure from density deviations. The density deviation can be computed explicitly or from a differential form. The deviation can be represented as a quotient or a difference of actual and rest density. One or more stiffness constants are involved. Some examples are: pi* = *k(ρi/ρ0 − 1), pi* = kk(ρ*i* − ρ0) or *pi* = *k1((ρi/ρ0)k2) - 1). As *pi* < ρ0 is not considered to solve the particle deficiency problem at the free surface, the computed pressure is always non-negative.15
Discretization of differential operator:
As for state equations, it requires density values, thus it would be efficient to compute them with densities altogether:
void ComputeDensitiesAndPressures(float* OutDensities,
float* OutPressures,
float* SortedPositions,
uint* GridParticleIndice,
uint* CellStarts,
uint* CellEnds,
uint NumParticles,
uint NumCells)
{
// thread per particle
uint NumThreads;
uint NumBlocks;
ComputeGridSize(NumParticles, 64u, NumBlocks, numThreads);
// execute the kernel
ComputeDensitiesAndPressuresDevice<<<NumBlocks, NumThreads>>>(OutDensities,
OutPressures
(float4*) SortedPositions,
GridParticleIndice,
CellStarts,
CellEnds,
NumParticles);
// check if kernel invocation generated an error
getLastCudaError("Kernel execution failed");
}
__global__
void ComputeDensitiesAndPressuresDevice(float* OutDensities, // output: new density
float* OutPressures, // output: new pressure
float4* SortedPositions, // input: sorted Positions
uint* GridParticleIndice, // input: sorted particle indices
uint* CellStarts,
uint* CellEnds,
uint NumParticles)
{
uint Index = (blockIdx.x * blockDim.x) + threadIdx.x;
...
// write new velocityocity back to original unsorted location
uint OriginalIndex = GridParticleIndice[Index];
OutDensities[OriginalIndex] = Density;
// state equation
// 0
// p = k(rho_i - rho_0)
// 1
// p = k((rho_i / rho_0) - 1)
// 2
// p = k((rho_i / rho_0)^7 - 1)
OutPressures[OriginalIndex] = gParameters.GasConst * (Density - gParameters.RestDensity);
}
Now we know the pressure field, we can compute the pressure force field. It would be more efficient if we compute all the forces in a single function.
void ComputeForces(float* OutPressureForces,
float* OutNonPressureForces,
float* OutVelocities,
float* SortedPositions,
float* SortedVelocities,
float* Densities,
float* Pressures,
uint* GridParticleIndice,
uint* CellStarts,
uint* CellEnds,
uint NumParticles,
uint NumCells)
{
// thread per particle
uint NumThreads;
uint NumBlocks;
ComputeGridSize(NumParticles, 64u, NumBlocks, NumThreads);
// execute the kernel
ComputeForcesDevice<<<NumBlocks, NumThreads>>>((float4*) OutPressureForces
(float4*) OutNonPressureForces
(float4*) OutVelocities,
(float4*) SortedPositions,
(float4*) SortedVelocities,
Densities,
Pressures,
DeltaTime,
GridParticleIndice,
CellStarts,
CellEnds,
NumParticles);
// check if kernel invocation generated an error
getLastCudaError("Kernel execution failed");
}
__global__
void ComputeForcesDevice(float4* OutNonPressureForces, // output: updated non pressure forces
float4* OutPressureForces, // output: updated pressure forces
float4* OutVelocities, // output: updated Velocities
float4* SortedPositions, // input: sorted Positions
float4* SortedVelocities,
float* Densities,
float* Pressures,
float DeltaTime,
uint* GridParticleIndice, // input: sorted particle indices
uint* CellStarts,
uint* CellEnds,
uint NumParticles)
{
uint Index = (blockIdx.x * blockDim.x) + threadIdx.x;
...
float Pressure = Pressures[OriginalIndex];
...
// examine neighbouring cells
float3 PressureForce = make_float3(0.0f);
...
for (int z = -1; z <= 1; z++)
{
for (int y = -1; y <= 1; y++)
{
for (int x = -1; x <= 1; x++)
{
int3 Neighbourpositionition = Gridpositionition + make_int3(x, y, z);
ComputeForcesByCell(Neighbourpositionition,
Index,
PressureForce,
ViscosityForce,
SurfaceTensionForce,
bShouldCalculateSurfaceTension,
positionition,
velocityocity,
Density,
Pressure,
SortedPositions,
SortedVelocities,
Densities,
Pressures,
GridParticleIndice,
CellStarts,
CellEnds);
}
}
}
...
PressureForce *= -gParameters.Mass
ViscosityForce *= -gParameters.Mass * gParameters.Viscosity;
float3 ExternalForce = gParameters.Mass * gParameters.Gravity;
OutPressureForces[OriginalIndex] = PressureForce;
OutNonPressureForce[OriginalIndex] = ViscosityForce + ExternalForce;
OutVelocities[OriginalIndex] += make_float4(((OutPressureForce[OriginalIndex] + OutNonPressureForce[OriginalIndex]) / gParameters.Mass) * DeltaTime, 0.0f);
}
__device__
void ComputeForcesByCell(int3 Gridpositionition,
uint Index,
float3& OutPressureForce,
float3& OutViscosityForce,
float3& OutSurfaceTensionForce,
bool bShouldCalculateSurfaceTension,
float3 positionition,
float3 velocityocity,
float Density,
float Pressure,
float4* SortedPositions,
float4* SortedVelocities,
float* Densities,
float* Pressures,
uint* GridParticleIndice,
uint* CellStarts,
uint* CellEnds)
{
...
for (uint j = StartIndex; j < EndIndex; j++)
{
if (j != Index) // check not colliding with self
{
float3 Neighborpositionition = make_float3(SortedPositions[j]);
float3 Rij = (positionition - Neighborpositionition);
//float r = length(rij);
float R2 = LengthSquared(Rij);
if (R2 < gParameters.KernelRadiusSquared)
{
uint OriginalIndex = GridParticleIndice[j];
float3 Neighborvelocityocity = make_float3(SortedVelocities[j]);
float3 Vij = velocityocity - Neighborvelocityocity;
// sigma mass_j * (pressure_i / (density_i)^2 + pressure_j / (density_j)^2) * gradient of W_ij
OutPressureForce += gParameters.Mass * ((Pressure / (Density * Density)) + (Pressures[OriginalIndex] / (Densities[OriginalIndex] * Densities[OriginalIndex]))) * SpikyKernelGradient(Rij);
...
}
}
...
}
Update Positions
Now we have acquired the Velocities which we can now calculate the Positions of each particles. However, we need to do one more additional step: boundary handling.
To keep it simple, we will imagine that there is an invisible box that surrounds the particles. The box is 2.0f in width, height, and depth.
After updating the position, we will check whether the position exceeds the limit. If so, then we will simply reverse the direction of the particle.
struct IntegrateFunctor
{
float DeltaTime;
__host__ __device__
IntegrateFunctor(float InDeltaTime)
: DeltaTime(InDeltatime)
{
}
template <typename Tuple>
__device__
void operator()(Tuple InTuple)
{
volatile float4 PositionData = thrust::get<0>(InTuple);
volatile float4 VelocityData = thrust::get<1>(InTuple);
float3 Position = make_float3(PositionData.x, PositionData.y, PositionData.z);
float3 Velocity = make_float3(VelocityData.x, VelocityData.y, VelocityData.z);
Position += Velocity * deltaTime;
if (Position.x > 1.0f * gParameters.XScaleFactor - gParameters.ParticleRadius)
{
Position.x = 1.0f * gParameters.XScaleFactor - gParameters.ParticleRadius;
Velocity.x *= gParameters.BoundaryDamping;
}
if (Position.x < -1.0f * gParameters.XScaleFactor + gParameters.ParticleRadius)
{
Position.x = -1.0f * gParameters.XScaleFactor + gParameters.ParticleRadius;
Velocity.x *= gParameters.BoundaryDamping;
}
if (Position.y > 1.0f * gParameters.YScaleFactor - gParameters.ParticleRadius)
{
Position.y = 1.0f * gParameters.YScaleFactor - gParameters.ParticleRadius;
Velocity.y *= gParameters.BoundaryDamping;
}
if (Position.z > 1.0f *gParameters. ZScaleFactor - gParameters.ParticleRadius)
{
Position.z = 1.0f * gParameters.ZScaleFactor - gParameters.ParticleRadius;
Velocity.z *= gParameters.BoundaryDamping;
}
if (Position.z < -1.0f * gParameters.ZScaleFactor + gParameters.ParticleRadius)
{
Position.z = -1.0f * gParameters.ZScaleFactor + gParameters.ParticleRadius;
Velocity.z *= gParameters.BoundaryDamping;
}
if (Position.y < -1.0f * gParameters.YScaleFactor + gParameters.ParticleRadius)
{
Position.y = -1.0f * gParameters.YScaleFactor + gParameters.ParticleRadius;
Velocity.y *= gParameters.BoundaryDamping;
}
// store new positionition and velocityocity
//printf("after positionition=(%f, %f, %f)\n", positionition.x, positionition.y, positionition.z);
thrust::get<0>(InTuple) = make_float4(Position, PositionData.w);
thrust::get<1>(InTuple) = make_float4(Velocity, VelocityData.w);
}
};
void IntegrateSystem(float* OutPositions, float* OutVelocities, float DeltaTime, uint NumParticles)
{
thrust::device_ptr<float4> devicePositions((float4*) OutPositions);
thrust::device_ptr<float4> deviceVelocities((float4*) OutVelocities);
thrust::for_each(thrust::make_zip_iterator(thrust::make_tuple(devicePositions, deviceVelocities)),
thrust::make_zip_iterator(thrust::make_tuple(devicePositions + NumParticles, deviceVelocities + NumParticles)),
IntegrateFunctor(deltaTime));
}
- Doyup Kim. 2016. Fluid Engine Develocityopment (1st. ed.). A K Peters/CRC Press, Natikc, MA.
- J. J. Monaghan. Smoothed particle hydrodynamics. Annual Review of Astronomy and Astrophysics 30:543-574, 1992.
- J. J. Monaghan. Simulating free surface flows with SPH. Journal of Computational Physics, 110(2):399–406, 1994.
- M. Desbrun, and M-P. Gascuel. Smoothed particles: A new paradigm for animating highly deformable bodies. In Computer Animation and Simulation’96, pages 61–76. Springer Vienna, 1996.
- M. Müller, D. Charypar, and M. Gross. Particle-based fluid simulation for interactive applications. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics Sympositionium on Computer Animation, pages 154–159, 2003.
- RealFlow 10 documentation. Available at https://nextlimitsupport.atlassian.net/wiki/spaces/rf2016docs/overview. Accessed on 27 NOV 2021.
- Kinematics - Wikipedia
- Continuum mechanics - Wikipedia
- Momentum - Wikipedia
- Lagrangian and Eulerian specification of the flow field - Wikipedia
- Navier-Stokes equations - Wikipedia
- McLean, Doug (2012). "Continuum Fluid Mechanics and the Navier-Stokes Equations". Understanding Aerodynamics: Arguing from the Real Physics. John Wiley & Sons. pp. 13–78. ISBN 9781119967514. The main relationships comprising the NS equations are the basic conservation laws for mass, momentum, and energy. To have a complete equation set we also need an equation of state relating temperature, pressure, and density...
- Batchelor (1967) pp. 142–148.
- Batchelor (1967) p. 165.
- Koschier, Dan, Jan Bender, Barbara Solenthaler, and Matthias Teschner. "Smoothed particle hydrodynamics techniques for the physics based simulation of fluids and solids." arXiv preprint arXiv:2009.06944 (2020).
- David Staubach , "Smoothed Particle Hydrodynamics Real-Time Fluid Simulation Approach." Friedrich-Alexander-Universitaet Erlangen-Nuernberg (2010).